Welcome to Subscribe On Youtube
3241. Time Taken to Mark All Nodes
Description
There exists an undirected tree with n nodes numbered 0 to n - 1. You are given a 2D integer array edges of length n - 1, where edges[i] = [ui, vi] indicates that there is an edge between nodes ui and vi in the tree.
Initially, all nodes are unmarked. For each node i:
- If
iis odd, the node will get marked at timexif there is at least one node adjacent to it which was marked at timex - 1. - If
iis even, the node will get marked at timexif there is at least one node adjacent to it which was marked at timex - 2.
Return an array times where times[i] is the time when all nodes get marked in the tree, if you mark node i at time t = 0.
Note that the answer for each times[i] is independent, i.e. when you mark node i all other nodes are unmarked.
Example 1:
Input: edges = [[0,1],[0,2]]
Output: [2,4,3]
Explanation:
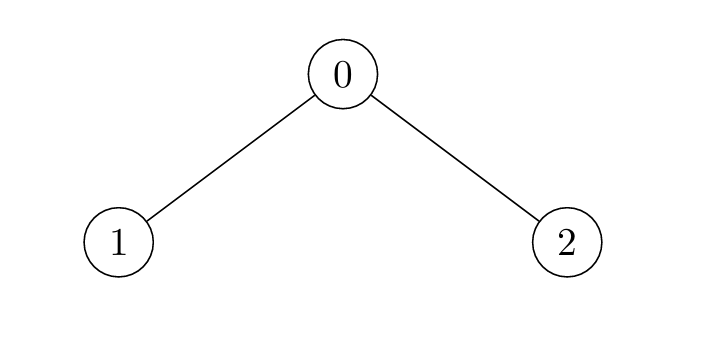
- For
i = 0:- Node 1 is marked at
t = 1, and Node 2 att = 2.
- Node 1 is marked at
- For
i = 1:- Node 0 is marked at
t = 2, and Node 2 att = 4.
- Node 0 is marked at
- For
i = 2:- Node 0 is marked at
t = 2, and Node 1 att = 3.
- Node 0 is marked at
Example 2:
Input: edges = [[0,1]]
Output: [1,2]
Explanation:
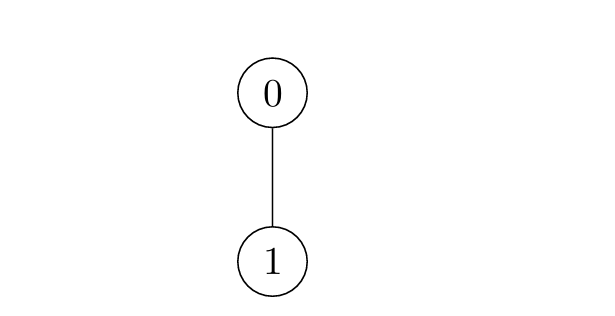
- For
i = 0:- Node 1 is marked at
t = 1.
- Node 1 is marked at
- For
i = 1:- Node 0 is marked at
t = 2.
- Node 0 is marked at
Example 3:
Input: edges = [[2,4],[0,1],[2,3],[0,2]]
Output: [4,6,3,5,5]
Explanation:

Constraints:
2 <= n <= 105edges.length == n - 1edges[i].length == 20 <= edges[i][0], edges[i][1] <= n - 1- The input is generated such that
edgesrepresents a valid tree.