2003. Smallest Missing Genetic Value in Each Subtree

Description

There is a family tree rooted at 0 consisting of n nodes numbered 0 to n - 1. You are given a 0-indexed integer array parents, where parents[i] is the parent for node i. Since node 0 is the root, parents[0] == -1.

There are 10⁵ genetic values, each represented by an integer in the inclusive range [1, 10⁵]. You are given a 0-indexed integer array nums, where nums[i] is a distinct genetic value for node i.

Return an array ans of length n where ans[i] is the smallest genetic value that is missing from the subtree rooted at node i.

The subtree rooted at a node x contains node x and all of its descendant nodes.

Example 1:

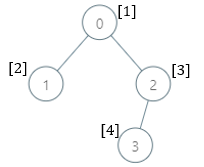
Input: parents = [-1,0,0,2], nums = [1,2,3,4]
Output: [5,1,1,1]
Explanation: The answer for each subtree is calculated as follows:
- 0: The subtree contains nodes [0,1,2,3] with values [1,2,3,4]. 5 is the smallest missing value.
- 1: The subtree contains only node 1 with value 2. 1 is the smallest missing value.
- 2: The subtree contains nodes [2,3] with values [3,4]. 1 is the smallest missing value.
- 3: The subtree contains only node 3 with value 4. 1 is the smallest missing value.

Example 2:

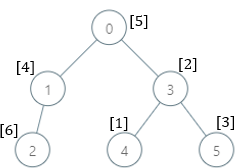
Input: parents = [-1,0,1,0,3,3], nums = [5,4,6,2,1,3]
Output: [7,1,1,4,2,1]
Explanation: The answer for each subtree is calculated as follows:
- 0: The subtree contains nodes [0,1,2,3,4,5] with values [5,4,6,2,1,3]. 7 is the smallest missing value.
- 1: The subtree contains nodes [1,2] with values [4,6]. 1 is the smallest missing value.
- 2: The subtree contains only node 2 with value 6. 1 is the smallest missing value.
- 3: The subtree contains nodes [3,4,5] with values [2,1,3]. 4 is the smallest missing value.
- 4: The subtree contains only node 4 with value 1. 2 is the smallest missing value.
- 5: The subtree contains only node 5 with value 3. 1 is the smallest missing value.

Example 3:

Input: parents = [-1,2,3,0,2,4,1], nums = [2,3,4,5,6,7,8]
Output: [1,1,1,1,1,1,1]
Explanation: The value 1 is missing from all the subtrees.

Constraints:

n == parents.length == nums.length
2 <= n <= 10⁵
0 <= parents[i] <= n - 1 for i != 0
parents[0] == -1
parents represents a valid tree.
1 <= nums[i] <= 10⁵
Each nums[i] is distinct.

Solutions

Solution 1: DFS

We notice that each node has a unique gene value, so we only need to find the node $idx$ with gene value $1$, and all nodes except for those on the path from node $idx$ to the root node $0$ have an answer of $1$.

Therefore, we initialize the answer array $ans$ to $[1,1,…,1]$, and our focus is on finding the answer for each node on the path from node $idx$ to the root node $0$.

We can start from node $idx$ and use depth-first search to mark the gene values that appear in the subtree rooted at $idx$, and record them in the array $has$. During the search process, we use an array $vis$ to mark the visited nodes to prevent repeated visits.

Next, we start from $i=2$ and keep looking for the first gene value that has not appeared, which is the answer for node $idx$. Here, $i$ is strictly increasing, because the gene values are unique, so we can always find a gene value that has not appeared in $[1,..n+1]$.

Then, we update the answer for node $idx$, i.e., $ans[idx]=i$, and update $idx$ to its parent node to continue the above process until $idx=-1$, which means we have reached the root node $0$.

Finally, we return the answer array $ans$.

The time complexity is $O(n)$, and the space complexity is $O(n)$. Here, $n$ is the number of nodes.

class Solution {
    private List<Integer>[] g;
    private boolean[] vis;
    private boolean[] has;
    private int[] nums;

    public int[] smallestMissingValueSubtree(int[] parents, int[] nums) {
        int n = nums.length;
        this.nums = nums;
        g = new List[n];
        vis = new boolean[n];
        has = new boolean[n + 2];
        Arrays.setAll(g, i -> new ArrayList<>());
        int idx = -1;
        for (int i = 0; i < n; ++i) {
            if (i > 0) {
                g[parents[i]].add(i);
            }
            if (nums[i] == 1) {
                idx = i;
            }
        }
        int[] ans = new int[n];
        Arrays.fill(ans, 1);
        if (idx == -1) {
            return ans;
        }
        for (int i = 2; idx != -1; idx = parents[idx]) {
            dfs(idx);
            while (has[i]) {
                ++i;
            }
            ans[idx] = i;
        }
        return ans;
    }

    private void dfs(int i) {
        if (vis[i]) {
            return;
        }
        vis[i] = true;
        if (nums[i] < has.length) {
            has[nums[i]] = true;
        }
        for (int j : g[i]) {
            dfs(j);
        }
    }
}

class Solution {
public:
    vector<int> smallestMissingValueSubtree(vector<int>& parents, vector<int>& nums) {
        int n = nums.size();
        vector<int> g[n];
        bool vis[n];
        bool has[n + 2];
        memset(vis, false, sizeof(vis));
        memset(has, false, sizeof(has));
        int idx = -1;
        for (int i = 0; i < n; ++i) {
            if (i) {
                g[parents[i]].push_back(i);
            }
            if (nums[i] == 1) {
                idx = i;
            }
        }
        vector<int> ans(n, 1);
        if (idx == -1) {
            return ans;
        }
        function<void(int)> dfs = [&](int i) {
            if (vis[i]) {
                return;
            }
            vis[i] = true;
            if (nums[i] < n + 2) {
                has[nums[i]] = true;
            }
            for (int j : g[i]) {
                dfs(j);
            }
        };
        for (int i = 2; ~idx; idx = parents[idx]) {
            dfs(idx);
            while (has[i]) {
                ++i;
            }
            ans[idx] = i;
        }
        return ans;
    }
};

class Solution:
    def smallestMissingValueSubtree(
        self, parents: List[int], nums: List[int]
    ) -> List[int]:
        def dfs(i: int):
            if vis[i]:
                return
            vis[i] = True
            if nums[i] < len(has):
                has[nums[i]] = True
            for j in g[i]:
                dfs(j)

        n = len(nums)
        ans = [1] * n
        g = [[] for _ in range(n)]
        idx = -1
        for i, p in enumerate(parents):
            if i:
                g[p].append(i)
            if nums[i] == 1:
                idx = i
        if idx == -1:
            return ans
        vis = [False] * n
        has = [False] * (n + 2)
        i = 2
        while idx != -1:
            dfs(idx)
            while has[i]:
                i += 1
            ans[idx] = i
            idx = parents[idx]
        return ans

func smallestMissingValueSubtree(parents []int, nums []int) []int {
	n := len(nums)
	g := make([][]int, n)
	vis := make([]bool, n)
	has := make([]bool, n+2)
	idx := -1
	ans := make([]int, n)
	for i, p := range parents {
		if i > 0 {
			g[p] = append(g[p], i)
		}
		if nums[i] == 1 {
			idx = i
		}
		ans[i] = 1
	}
	if idx < 0 {
		return ans
	}
	var dfs func(int)
	dfs = func(i int) {
		if vis[i] {
			return
		}
		vis[i] = true
		if nums[i] < len(has) {
			has[nums[i]] = true
		}
		for _, j := range g[i] {
			dfs(j)
		}
	}
	for i := 2; idx != -1; idx = parents[idx] {
		dfs(idx)
		for has[i] {
			i++
		}
		ans[idx] = i
	}
	return ans
}

function smallestMissingValueSubtree(parents: number[], nums: number[]): number[] {
    const n = nums.length;
    const g: number[][] = Array.from({ length: n }, () => []);
    const vis: boolean[] = Array(n).fill(false);
    const has: boolean[] = Array(n + 2).fill(false);
    const ans: number[] = Array(n).fill(1);
    let idx = -1;
    for (let i = 0; i < n; ++i) {
        if (i) {
            g[parents[i]].push(i);
        }
        if (nums[i] === 1) {
            idx = i;
        }
    }
    if (idx === -1) {
        return ans;
    }
    const dfs = (i: number): void => {
        if (vis[i]) {
            return;
        }
        vis[i] = true;
        if (nums[i] < has.length) {
            has[nums[i]] = true;
        }
        for (const j of g[i]) {
            dfs(j);
        }
    };
    for (let i = 2; ~idx; idx = parents[idx]) {
        dfs(idx);
        while (has[i]) {
            ++i;
        }
        ans[idx] = i;
    }
    return ans;
}

impl Solution {
    pub fn smallest_missing_value_subtree(parents: Vec<i32>, nums: Vec<i32>) -> Vec<i32> {
        fn dfs(
            i: usize,
            vis: &mut Vec<bool>,
            has: &mut Vec<bool>,
            g: &Vec<Vec<usize>>,
            nums: &Vec<i32>
        ) {
            if vis[i] {
                return;
            }
            vis[i] = true;
            if nums[i] < (has.len() as i32) {
                has[nums[i] as usize] = true;
            }
            for &j in &g[i] {
                dfs(j, vis, has, g, nums);
            }
        }

        let n = nums.len();
        let mut ans = vec![1; n];
        let mut g: Vec<Vec<usize>> = vec![vec![]; n];
        let mut idx = -1;
        for (i, &p) in parents.iter().enumerate() {
            if i > 0 {
                g[p as usize].push(i);
            }
            if nums[i] == 1 {
                idx = i as i32;
            }
        }
        if idx == -1 {
            return ans;
        }
        let mut vis = vec![false; n];
        let mut has = vec![false; (n + 2) as usize];
        let mut i = 2;
        let mut idx_mut = idx;
        while idx_mut != -1 {
            dfs(idx_mut as usize, &mut vis, &mut has, &g, &nums);
            while has[i] {
                i += 1;
            }
            ans[idx_mut as usize] = i as i32;
            idx_mut = parents[idx_mut as usize];
        }
        ans
    }
}

2003 - Smallest Missing Genetic Value in Each Subtree

2003. Smallest Missing Genetic Value in Each Subtree

Description

Solutions

All Problems

All Solutions

Welcome to Subscribe On Youtube

2003. Smallest Missing Genetic Value in Each Subtree

Description

Solutions

All Problems

All Solutions