Welcome to Subscribe On Youtube
2002. Maximum Product of the Length of Two Palindromic Subsequences
Description
Given a string s, find two disjoint palindromic subsequences of s such that the product of their lengths is maximized. The two subsequences are disjoint if they do not both pick a character at the same index.
Return the maximum possible product of the lengths of the two palindromic subsequences.
A subsequence is a string that can be derived from another string by deleting some or no characters without changing the order of the remaining characters. A string is palindromic if it reads the same forward and backward.
Example 1:
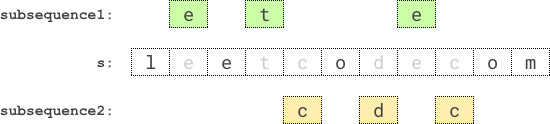
Input: s = "leetcodecom" Output: 9 Explanation: An optimal solution is to choose "ete" for the 1st subsequence and "cdc" for the 2nd subsequence. The product of their lengths is: 3 * 3 = 9.
Example 2:
Input: s = "bb" Output: 1 Explanation: An optimal solution is to choose "b" (the first character) for the 1st subsequence and "b" (the second character) for the 2nd subsequence. The product of their lengths is: 1 * 1 = 1.
Example 3:
Input: s = "accbcaxxcxx" Output: 25 Explanation: An optimal solution is to choose "accca" for the 1st subsequence and "xxcxx" for the 2nd subsequence. The product of their lengths is: 5 * 5 = 25.
Constraints:
2 <= s.length <= 12sconsists of lowercase English letters only.
Solutions
Solution 1: Binary Enumeration
We notice that the length of the string $s$ does not exceed $12$, so we can use the method of binary enumeration to enumerate all subsequences of $s$. Suppose the length of $s$ is $n$, we can use $2^n$ binary numbers of length $n$ to represent all subsequences of $s$. For each binary number, the $i$-th bit being $1$ means the $i$-th character of $s$ is in the subsequence, and $0$ means it is not in the subsequence. For each binary number, we judge whether it is a palindrome subsequence and record it in the array $p$.
Next, we enumerate each number $i$ in $p$. If $i$ is a palindrome subsequence, then we can enumerate a number $j$ from the complement of $i$, $mx = (2^n - 1) \oplus i$. If $j$ is also a palindrome subsequence, then $i$ and $j$ are the two palindrome subsequences we are looking for. Their lengths are the number of $1$s in the binary representation of $i$ and $j$, denoted as $a$ and $b$, respectively. Then their product is $a \times b$. We take the maximum of all possible $a \times b$.
The time complexity is $(2^n \times n + 3^n)$, and the space complexity is $O(2^n)$. Here, $n$ is the length of the string $s$.
-
class Solution { public int maxProduct(String s) { int n = s.length(); boolean[] p = new boolean[1 << n]; Arrays.fill(p, true); for (int k = 1; k < 1 << n; ++k) { for (int i = 0, j = n - 1; i < n; ++i, --j) { while (i < j && (k >> i & 1) == 0) { ++i; } while (i < j && (k >> j & 1) == 0) { --j; } if (i < j && s.charAt(i) != s.charAt(j)) { p[k] = false; break; } } } int ans = 0; for (int i = 1; i < 1 << n; ++i) { if (p[i]) { int a = Integer.bitCount(i); int mx = ((1 << n) - 1) ^ i; for (int j = mx; j > 0; j = (j - 1) & mx) { if (p[j]) { int b = Integer.bitCount(j); ans = Math.max(ans, a * b); } } } } return ans; } } -
class Solution { public: int maxProduct(string s) { int n = s.size(); vector<bool> p(1 << n, true); for (int k = 1; k < 1 << n; ++k) { for (int i = 0, j = n - 1; i < j; ++i, --j) { while (i < j && !(k >> i & 1)) { ++i; } while (i < j && !(k >> j & 1)) { --j; } if (i < j && s[i] != s[j]) { p[k] = false; break; } } } int ans = 0; for (int i = 1; i < 1 << n; ++i) { if (p[i]) { int a = __builtin_popcount(i); int mx = ((1 << n) - 1) ^ i; for (int j = mx; j; j = (j - 1) & mx) { if (p[j]) { int b = __builtin_popcount(j); ans = max(ans, a * b); } } } } return ans; } }; -
class Solution: def maxProduct(self, s: str) -> int: n = len(s) p = [True] * (1 << n) for k in range(1, 1 << n): i, j = 0, n - 1 while i < j: while i < j and (k >> i & 1) == 0: i += 1 while i < j and (k >> j & 1) == 0: j -= 1 if i < j and s[i] != s[j]: p[k] = False break i, j = i + 1, j - 1 ans = 0 for i in range(1, 1 << n): if p[i]: mx = ((1 << n) - 1) ^ i j = mx a = i.bit_count() while j: if p[j]: b = j.bit_count() ans = max(ans, a * b) j = (j - 1) & mx return ans -
func maxProduct(s string) (ans int) { n := len(s) p := make([]bool, 1<<n) for i := range p { p[i] = true } for k := 1; k < 1<<n; k++ { for i, j := 0, n-1; i < j; i, j = i+1, j-1 { for i < j && (k>>i&1) == 0 { i++ } for i < j && (k>>j&1) == 0 { j-- } if i < j && s[i] != s[j] { p[k] = false break } } } for i := 1; i < 1<<n; i++ { if p[i] { a := bits.OnesCount(uint(i)) mx := (1<<n - 1) ^ i for j := mx; j > 0; j = (j - 1) & mx { if p[j] { b := bits.OnesCount(uint(j)) ans = max(ans, a*b) } } } } return }