1632. Rank Transform of a Matrix

Description

Given an m x n matrix, return a new matrix answer where answer[row][col] is the rank of matrix[row][col].

The rank is an integer that represents how large an element is compared to other elements. It is calculated using the following rules:

The rank is an integer starting from 1.
If two elements p and q are in the same row or column, then:
- If p < q then rank(p) < rank(q)
- If p == q then rank(p) == rank(q)
- If p > q then rank(p) > rank(q)
The rank should be as small as possible.

The test cases are generated so that answer is unique under the given rules.

Example 1:

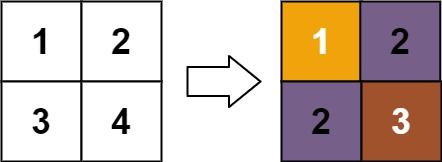
Input: matrix = [[1,2],[3,4]]
Output: [[1,2],[2,3]]
Explanation:
The rank of matrix[0][0] is 1 because it is the smallest integer in its row and column.
The rank of matrix[0][1] is 2 because matrix[0][1] > matrix[0][0] and matrix[0][0] is rank 1.
The rank of matrix[1][0] is 2 because matrix[1][0] > matrix[0][0] and matrix[0][0] is rank 1.
The rank of matrix[1][1] is 3 because matrix[1][1] > matrix[0][1], matrix[1][1] > matrix[1][0], and both matrix[0][1] and matrix[1][0] are rank 2.

Example 2:

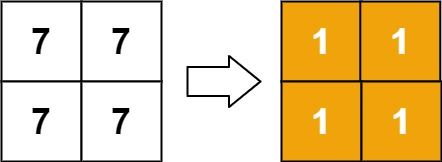
Input: matrix = [[7,7],[7,7]]
Output: [[1,1],[1,1]]

Example 3:

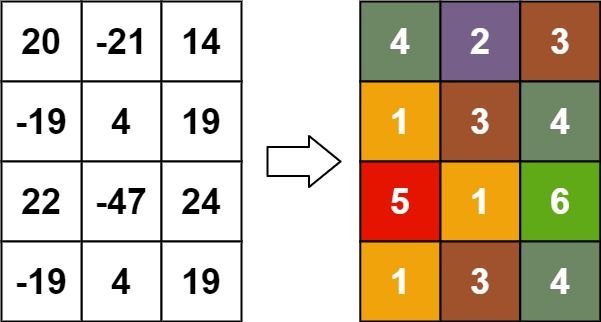
Input: matrix = [[20,-21,14],[-19,4,19],[22,-47,24],[-19,4,19]]
Output: [[4,2,3],[1,3,4],[5,1,6],[1,3,4]]

Constraints:

m == matrix.length
n == matrix[i].length
1 <= m, n <= 500
-10⁹ <= matrix[row][col] <= 10⁹

Solutions

class UnionFind {
    private int[] p;
    private int[] size;

    public UnionFind(int n) {
        p = new int[n];
        size = new int[n];
        for (int i = 0; i < n; ++i) {
            p[i] = i;
            size[i] = 1;
        }
    }

    public int find(int x) {
        if (p[x] != x) {
            p[x] = find(p[x]);
        }
        return p[x];
    }

    public void union(int a, int b) {
        int pa = find(a), pb = find(b);
        if (pa != pb) {
            if (size[pa] > size[pb]) {
                p[pb] = pa;
                size[pa] += size[pb];
            } else {
                p[pa] = pb;
                size[pb] += size[pa];
            }
        }
    }

    public void reset(int x) {
        p[x] = x;
        size[x] = 1;
    }
}

class Solution {
    public int[][] matrixRankTransform(int[][] matrix) {
        int m = matrix.length, n = matrix[0].length;
        TreeMap<Integer, List<int[]>> d = new TreeMap<>();
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                d.computeIfAbsent(matrix[i][j], k -> new ArrayList<>()).add(new int[] {i, j});
            }
        }
        int[] rowMax = new int[m];
        int[] colMax = new int[n];
        int[][] ans = new int[m][n];
        UnionFind uf = new UnionFind(m + n);
        int[] rank = new int[m + n];
        for (var ps : d.values()) {
            for (var p : ps) {
                uf.union(p[0], p[1] + m);
            }
            for (var p : ps) {
                int i = p[0], j = p[1];
                rank[uf.find(i)] = Math.max(rank[uf.find(i)], Math.max(rowMax[i], colMax[j]));
            }
            for (var p : ps) {
                int i = p[0], j = p[1];
                ans[i][j] = 1 + rank[uf.find(i)];
                rowMax[i] = ans[i][j];
                colMax[j] = ans[i][j];
            }
            for (var p : ps) {
                uf.reset(p[0]);
                uf.reset(p[1] + m);
            }
        }
        return ans;
    }
}

class UnionFind {
public:
    UnionFind(int n) {
        p = vector<int>(n);
        size = vector<int>(n, 1);
        iota(p.begin(), p.end(), 0);
    }

    void unite(int a, int b) {
        int pa = find(a), pb = find(b);
        if (pa != pb) {
            if (size[pa] > size[pb]) {
                p[pb] = pa;
                size[pa] += size[pb];
            } else {
                p[pa] = pb;
                size[pb] += size[pa];
            }
        }
    }

    int find(int x) {
        if (p[x] != x) {
            p[x] = find(p[x]);
        }
        return p[x];
    }

    void reset(int x) {
        p[x] = x;
        size[x] = 1;
    }

private:
    vector<int> p, size;
};

class Solution {
public:
    vector<vector<int>> matrixRankTransform(vector<vector<int>>& matrix) {
        int m = matrix.size(), n = matrix[0].size();
        map<int, vector<pair<int, int>>> d;
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                d[matrix[i][j]].push_back({i, j});
            }
        }
        vector<int> rowMax(m);
        vector<int> colMax(n);
        vector<vector<int>> ans(m, vector<int>(n));
        UnionFind uf(m + n);
        vector<int> rank(m + n);
        for (auto& [_, ps] : d) {
            for (auto& [i, j] : ps) {
                uf.unite(i, j + m);
            }
            for (auto& [i, j] : ps) {
                rank[uf.find(i)] = max({rank[uf.find(i)], rowMax[i], colMax[j]});
            }
            for (auto& [i, j] : ps) {
                ans[i][j] = rowMax[i] = colMax[j] = 1 + rank[uf.find(i)];
            }
            for (auto& [i, j] : ps) {
                uf.reset(i);
                uf.reset(j + m);
            }
        }
        return ans;
    }
};

class UnionFind:
    def __init__(self, n):
        self.p = list(range(n))
        self.size = [1] * n

    def find(self, x):
        if self.p[x] != x:
            self.p[x] = self.find(self.p[x])
        return self.p[x]

    def union(self, a, b):
        pa, pb = self.find(a), self.find(b)
        if pa != pb:
            if self.size[pa] > self.size[pb]:
                self.p[pb] = pa
                self.size[pa] += self.size[pb]
            else:
                self.p[pa] = pb
                self.size[pb] += self.size[pa]

    def reset(self, x):
        self.p[x] = x
        self.size[x] = 1


class Solution:
    def matrixRankTransform(self, matrix: List[List[int]]) -> List[List[int]]:
        m, n = len(matrix), len(matrix[0])
        d = defaultdict(list)
        for i, row in enumerate(matrix):
            for j, v in enumerate(row):
                d[v].append((i, j))
        row_max = [0] * m
        col_max = [0] * n
        ans = [[0] * n for _ in range(m)]
        uf = UnionFind(m + n)
        for v in sorted(d):
            rank = defaultdict(int)
            for i, j in d[v]:
                uf.union(i, j + m)
            for i, j in d[v]:
                rank[uf.find(i)] = max(rank[uf.find(i)], row_max[i], col_max[j])
            for i, j in d[v]:
                ans[i][j] = row_max[i] = col_max[j] = 1 + rank[uf.find(i)]
            for i, j in d[v]:
                uf.reset(i)
                uf.reset(j + m)
        return ans

type unionFind struct {
	p, size []int
}

func newUnionFind(n int) *unionFind {
	p := make([]int, n)
	size := make([]int, n)
	for i := range p {
		p[i] = i
		size[i] = 1
	}
	return &unionFind{p, size}
}

func (uf *unionFind) find(x int) int {
	if uf.p[x] != x {
		uf.p[x] = uf.find(uf.p[x])
	}
	return uf.p[x]
}

func (uf *unionFind) union(a, b int) {
	pa, pb := uf.find(a), uf.find(b)
	if pa != pb {
		if uf.size[pa] > uf.size[pb] {
			uf.p[pb] = pa
			uf.size[pa] += uf.size[pb]
		} else {
			uf.p[pa] = pb
			uf.size[pb] += uf.size[pa]
		}
	}
}

func (uf *unionFind) reset(x int) {
	uf.p[x] = x
	uf.size[x] = 1
}

func matrixRankTransform(matrix [][]int) [][]int {
	m, n := len(matrix), len(matrix[0])
	type pair struct{ i, j int }
	d := map[int][]pair{}
	for i, row := range matrix {
		for j, v := range row {
			d[v] = append(d[v], pair{i, j})
		}
	}
	rowMax := make([]int, m)
	colMax := make([]int, n)
	ans := make([][]int, m)
	for i := range ans {
		ans[i] = make([]int, n)
	}
	vs := []int{}
	for v := range d {
		vs = append(vs, v)
	}
	sort.Ints(vs)
	uf := newUnionFind(m + n)
	rank := make([]int, m+n)
	for _, v := range vs {
		ps := d[v]
		for _, p := range ps {
			uf.union(p.i, p.j+m)
		}
		for _, p := range ps {
			i, j := p.i, p.j
			rank[uf.find(i)] = max(rank[uf.find(i)], max(rowMax[i], colMax[j]))
		}
		for _, p := range ps {
			i, j := p.i, p.j
			ans[i][j] = 1 + rank[uf.find(i)]
			rowMax[i], colMax[j] = ans[i][j], ans[i][j]
		}
		for _, p := range ps {
			uf.reset(p.i)
			uf.reset(p.j + m)
		}
	}
	return ans
}

1632 - Rank Transform of a Matrix

1632. Rank Transform of a Matrix

Description

Solutions

All Problems

All Solutions

Welcome to Subscribe On Youtube

1632. Rank Transform of a Matrix

Description

Solutions

All Problems

All Solutions