1631. Path With Minimum Effort

Description

You are a hiker preparing for an upcoming hike. You are given heights, a 2D array of size rows x columns, where heights[row][col] represents the height of cell (row, col). You are situated in the top-left cell, (0, 0), and you hope to travel to the bottom-right cell, (rows-1, columns-1) (i.e., 0-indexed). You can move up, down, left, or right, and you wish to find a route that requires the minimum effort.

A route's effort is the maximum absolute difference in heights between two consecutive cells of the route.

Return the minimum effort required to travel from the top-left cell to the bottom-right cell.

Example 1:

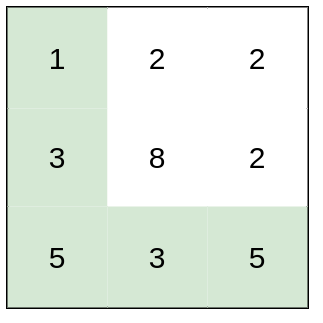
Input: heights = [[1,2,2],[3,8,2],[5,3,5]]
Output: 2
Explanation: The route of [1,3,5,3,5] has a maximum absolute difference of 2 in consecutive cells.
This is better than the route of [1,2,2,2,5], where the maximum absolute difference is 3.

Example 2:

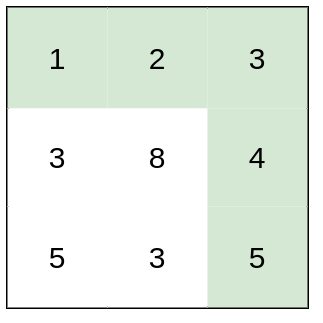
Input: heights = [[1,2,3],[3,8,4],[5,3,5]]
Output: 1
Explanation: The route of [1,2,3,4,5] has a maximum absolute difference of 1 in consecutive cells, which is better than route [1,3,5,3,5].

Example 3:

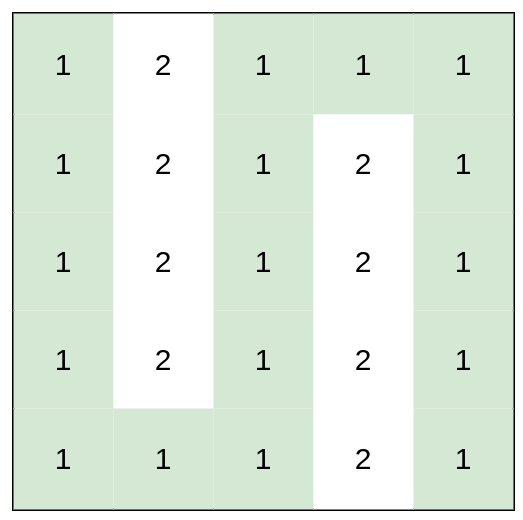
Input: heights = [[1,2,1,1,1],[1,2,1,2,1],[1,2,1,2,1],[1,2,1,2,1],[1,1,1,2,1]]
Output: 0
Explanation: This route does not require any effort.

Constraints:

rows == heights.length
columns == heights[i].length
1 <= rows, columns <= 100
1 <= heights[i][j] <= 10⁶

Solutions

Solution 1: Union-Find

For this problem, we can treat each cell as a node in a graph, and the absolute difference in height between two adjacent cells as the weight of the edge. Therefore, this problem is to solve the connectivity problem from the top-left node to the bottom-right node.

We first construct a set of edges, then sort them in ascending order of edge weight, and add edges one by one until the top-left node and the bottom-right node are connected. At this point, the weight of the edge is the minimum physical consumption value required by the problem.

The time complexity is $O(m \times n \times \log(m \times n))$, and the space complexity is $O(m \times n)$. Here, $m$ and $n$ are the number of rows and columns in the two-dimensional array, respectively.

Solution 2: Binary Search + BFS

We notice that if the maximum physical consumption value of a path is $x$, then for any $y > x$, this path also meets the conditions. This shows monotonicity, so we can use the binary search method to find the minimum physical consumption value that meets the conditions.

We define the left boundary of the binary search as $l=0$, and the right boundary as $r=10^6$. Each time we take $mid=(l+r)/2$, then use BFS to determine whether there is a path from the top-left corner to the bottom-right corner, so that the absolute difference in height between adjacent nodes on the path is not greater than $mid$. If it exists, it means that $mid$ may still be the minimum physical consumption value that meets the conditions, so we set $r=mid$, otherwise we set $l=mid+1$.

The time complexity is $O(m \times n \times \log M)$, and the space complexity is $O(m \times n)$. Here, $m$ and $n$ are the number of rows and columns in the two-dimensional array, respectively, and $M$ is the maximum value in the two-dimensional array. In this problem, $M=10^6$.

Solution 3: Heap-optimized Dijkstra Algorithm

We can treat each cell as a node in a graph, and the absolute difference in height between two adjacent cells as the weight of the edge. Therefore, this problem is to solve the shortest path problem from the top-left node to the bottom-right node.

We can use the Dijkstra algorithm to solve the shortest path problem, and use a priority queue (heap) to optimize the time complexity. Specifically, we maintain a two-dimensional array $dist$ of size $m \times n$, where $dist[i][j]$ represents the maximum weight of the shortest path from the top-left corner to the node $(i,j)$. Initially, $dist[0][0]=0$, and all other elements are positive infinity.

We use a priority queue (heap) to store nodes, and each time we take out the node with the smallest weight from the priority queue (heap), then update the weights of its adjacent nodes. If the weight of an adjacent node changes, then we add this node to the priority queue (heap). When the priority queue (heap) is empty, it means that we have found the shortest path.

class UnionFind {
    private final int[] p;
    private final int[] size;

    public UnionFind(int n) {
        p = new int[n];
        size = new int[n];
        for (int i = 0; i < n; ++i) {
            p[i] = i;
            size[i] = 1;
        }
    }

    public int find(int x) {
        if (p[x] != x) {
            p[x] = find(p[x]);
        }
        return p[x];
    }

    public boolean union(int a, int b) {
        int pa = find(a), pb = find(b);
        if (pa == pb) {
            return false;
        }
        if (size[pa] > size[pb]) {
            p[pb] = pa;
            size[pa] += size[pb];
        } else {
            p[pa] = pb;
            size[pb] += size[pa];
        }
        return true;
    }

    public boolean connected(int a, int b) {
        return find(a) == find(b);
    }
}

class Solution {
    public int minimumEffortPath(int[][] heights) {
        int m = heights.length, n = heights[0].length;
        UnionFind uf = new UnionFind(m * n);
        List<int[]> edges = new ArrayList<>();
        int[] dirs = {1, 0, 1};
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                for (int k = 0; k < 2; ++k) {
                    int x = i + dirs[k], y = j + dirs[k + 1];
                    if (x >= 0 && x < m && y >= 0 && y < n) {
                        int d = Math.abs(heights[i][j] - heights[x][y]);
                        edges.add(new int[] {d, i * n + j, x * n + y});
                    }
                }
            }
        }
        Collections.sort(edges, (a, b) -> a[0] - b[0]);
        for (int[] e : edges) {
            uf.union(e[1], e[2]);
            if (uf.connected(0, m * n - 1)) {
                return e[0];
            }
        }
        return 0;
    }
}

class UnionFind {
public:
    UnionFind(int n) {
        p = vector<int>(n);
        size = vector<int>(n, 1);
        iota(p.begin(), p.end(), 0);
    }

    bool unite(int a, int b) {
        int pa = find(a), pb = find(b);
        if (pa == pb) {
            return false;
        }
        if (size[pa] > size[pb]) {
            p[pb] = pa;
            size[pa] += size[pb];
        } else {
            p[pa] = pb;
            size[pb] += size[pa];
        }
        return true;
    }

    int find(int x) {
        if (p[x] != x) {
            p[x] = find(p[x]);
        }
        return p[x];
    }

    bool connected(int a, int b) {
        return find(a) == find(b);
    }

private:
    vector<int> p, size;
};

class Solution {
public:
    int minimumEffortPath(vector<vector<int>>& heights) {
        int m = heights.size(), n = heights[0].size();
        vector<array<int, 3>> edges;
        int dirs[3] = {0, 1, 0};
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                for (int k = 0; k < 2; ++k) {
                    int x = i + dirs[k], y = j + dirs[k + 1];
                    if (x >= 0 && x < m && y >= 0 && y < n) {
                        edges.push_back({abs(heights[i][j] - heights[x][y]), i * n + j, x * n + y});
                    }
                }
            }
        }
        sort(edges.begin(), edges.end());
        UnionFind uf(m * n);
        for (auto& [h, a, b] : edges) {
            uf.unite(a, b);
            if (uf.connected(0, m * n - 1)) {
                return h;
            }
        }
        return 0;
    }
};

class UnionFind:
    def __init__(self, n):
        self.p = list(range(n))
        self.size = [1] * n

    def find(self, x):
        if self.p[x] != x:
            self.p[x] = self.find(self.p[x])
        return self.p[x]

    def union(self, a, b):
        pa, pb = self.find(a), self.find(b)
        if pa == pb:
            return False
        if self.size[pa] > self.size[pb]:
            self.p[pb] = pa
            self.size[pa] += self.size[pb]
        else:
            self.p[pa] = pb
            self.size[pb] += self.size[pa]
        return True

    def connected(self, a, b):
        return self.find(a) == self.find(b)


class Solution:
    def minimumEffortPath(self, heights: List[List[int]]) -> int:
        m, n = len(heights), len(heights[0])
        uf = UnionFind(m * n)
        e = []
        dirs = (0, 1, 0)
        for i in range(m):
            for j in range(n):
                for a, b in pairwise(dirs):
                    x, y = i + a, j + b
                    if 0 <= x < m and 0 <= y < n:
                        e.append(
                            (abs(heights[i][j] - heights[x][y]), i * n + j, x * n + y)
                        )
        e.sort()
        for h, a, b in e:
            uf.union(a, b)
            if uf.connected(0, m * n - 1):
                return h
        return 0

type unionFind struct {
	p, size []int
}

func newUnionFind(n int) *unionFind {
	p := make([]int, n)
	size := make([]int, n)
	for i := range p {
		p[i] = i
		size[i] = 1
	}
	return &unionFind{p, size}
}

func (uf *unionFind) find(x int) int {
	if uf.p[x] != x {
		uf.p[x] = uf.find(uf.p[x])
	}
	return uf.p[x]
}

func (uf *unionFind) union(a, b int) bool {
	pa, pb := uf.find(a), uf.find(b)
	if pa == pb {
		return false
	}
	if uf.size[pa] > uf.size[pb] {
		uf.p[pb] = pa
		uf.size[pa] += uf.size[pb]
	} else {
		uf.p[pa] = pb
		uf.size[pb] += uf.size[pa]
	}
	return true
}

func (uf *unionFind) connected(a, b int) bool {
	return uf.find(a) == uf.find(b)
}

func minimumEffortPath(heights [][]int) int {
	m, n := len(heights), len(heights[0])
	edges := make([][3]int, 0, m*n*2)
	dirs := [3]int{0, 1, 0}
	for i, row := range heights {
		for j, h := range row {
			for k := 0; k < 2; k++ {
				x, y := i+dirs[k], j+dirs[k+1]
				if x >= 0 && x < m && y >= 0 && y < n {
					edges = append(edges, [3]int{abs(h - heights[x][y]), i*n + j, x*n + y})
				}
			}
		}
	}
	sort.Slice(edges, func(i, j int) bool { return edges[i][0] < edges[j][0] })
	uf := newUnionFind(m * n)
	for _, e := range edges {
		uf.union(e[1], e[2])
		if uf.connected(0, m*n-1) {
			return e[0]
		}
	}
	return 0
}

func abs(x int) int {
	if x < 0 {
		return -x
	}
	return x
}

class UnionFind {
    private p: number[];
    private size: number[];

    constructor(n: number) {
        this.p = Array.from({ length: n }, (_, i) => i);
        this.size = Array(n).fill(1);
    }

    find(x: number): number {
        if (this.p[x] !== x) {
            this.p[x] = this.find(this.p[x]);
        }
        return this.p[x];
    }

    union(a: number, b: number): boolean {
        const pa = this.find(a);
        const pb = this.find(b);
        if (pa === pb) {
            return false;
        }
        if (this.size[pa] > this.size[pb]) {
            this.p[pb] = pa;
            this.size[pa] += this.size[pb];
        } else {
            this.p[pa] = pb;
            this.size[pb] += this.size[pa];
        }
        return true;
    }

    connected(a: number, b: number): boolean {
        return this.find(a) === this.find(b);
    }
}

function minimumEffortPath(heights: number[][]): number {
    const m = heights.length;
    const n = heights[0].length;
    const uf = new UnionFind(m * n);
    const edges: number[][] = [];
    const dirs = [1, 0, 1];

    for (let i = 0; i < m; ++i) {
        for (let j = 0; j < n; ++j) {
            for (let k = 0; k < 2; ++k) {
                const x = i + dirs[k];
                const y = j + dirs[k + 1];
                if (x >= 0 && x < m && y >= 0 && y < n) {
                    const d = Math.abs(heights[i][j] - heights[x][y]);
                    edges.push([d, i * n + j, x * n + y]);
                }
            }
        }
    }

    edges.sort((a, b) => a[0] - b[0]);

    for (const [h, a, b] of edges) {
        uf.union(a, b);
        if (uf.connected(0, m * n - 1)) {
            return h;
        }
    }

    return 0;
}

1631 - Path With Minimum Effort

1631. Path With Minimum Effort

Description

Solutions

All Problems

All Solutions

Welcome to Subscribe On Youtube

1631. Path With Minimum Effort

Description

Solutions

All Problems

All Solutions