Welcome to Subscribe On Youtube
1628. Design an Expression Tree With Evaluate Function
Description
Given the postfix tokens of an arithmetic expression, build and return the binary expression tree that represents this expression.
Postfix notation is a notation for writing arithmetic expressions in which the operands (numbers) appear before their operators. For example, the postfix tokens of the expression 4*(5-(7+2)) are represented in the array postfix = ["4","5","7","2","+","-","*"].
The class Node is an interface you should use to implement the binary expression tree. The returned tree will be tested using the evaluate function, which is supposed to evaluate the tree's value. You should not remove the Node class; however, you can modify it as you wish, and you can define other classes to implement it if needed.
A binary expression tree is a kind of binary tree used to represent arithmetic expressions. Each node of a binary expression tree has either zero or two children. Leaf nodes (nodes with 0 children) correspond to operands (numbers), and internal nodes (nodes with two children) correspond to the operators '+' (addition), '-' (subtraction), '*' (multiplication), and '/' (division).
It's guaranteed that no subtree will yield a value that exceeds 109 in absolute value, and all the operations are valid (i.e., no division by zero).
Follow up: Could you design the expression tree such that it is more modular? For example, is your design able to support additional operators without making changes to your existing evaluate implementation?
Example 1:
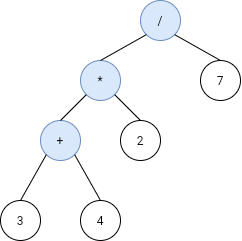
Input: s = ["3","4","+","2","*","7","/"]
Output: 2
Explanation: this expression evaluates to the above binary tree with expression ((3+4)*2)/7) = 14/7 = 2.
Example 2:

Input: s = ["4","5","2","7","+","-","*"]
Output: -16
Explanation: this expression evaluates to the above binary tree with expression 4*(5-(2+7)) = 4*(-4) = -16.
Constraints:
1 <= s.length < 100s.lengthis odd.sconsists of numbers and the characters'+','-','*', and'/'.- If
s[i]is a number, its integer representation is no more than105. - It is guaranteed that
sis a valid expression. - The absolute value of the result and intermediate values will not exceed
109. - It is guaranteed that no expression will include division by zero.
Solutions
Diff from 1597-Build-Binary-Expression-Tree-From-Infix-Expression is, there is no brackets () in expression, so making it easier to evaluate.
The analysis of postfix expressions is relatively easy. As for the evaluate method, it can be implemented recursively.
If the current node is a value, the value is returned directly, otherwise the left and right subtrees are calculated recursively, and then the operation of the tree root is calculated, and finally returned.
Follow up: Could you design the expression tree such that it is more modular? For example, is your design able to support additional operators without making changes to your existing evaluate implementation?
Just separate Node and Tree into 2 classes, then operators are on each Node, while Tree will not be affect.
-
/** * This is the interface for the expression tree Node. * You should not remove it, and you can define some classes to implement it. */ abstract class Node { public abstract int evaluate(); // define your fields here protected String val; protected Node left; protected Node right; }; class MyNode extends Node { public MyNode(String val) { this.val = val; } public int evaluate() { if (isNumeric()) { return Integer.parseInt(val); } int leftVal = left.evaluate(); int rightVal = right.evaluate(); if (Objects.equals(val, "+")) { return leftVal + rightVal; } if (Objects.equals(val, "-")) { return leftVal - rightVal; } if (Objects.equals(val, "*")) { return leftVal * rightVal; } if (Objects.equals(val, "/")) { return leftVal / rightVal; } return 0; } public boolean isNumeric() { for (char c : val.toCharArray()) { if (!Character.isDigit(c)) { return false; } } return true; } } /** * This is the TreeBuilder class. * You can treat it as the driver code that takes the postinfix input * and returns the expression tree represnting it as a Node. */ class TreeBuilder { Node buildTree(String[] postfix) { Deque<MyNode> stk = new ArrayDeque<>(); for (String s : postfix) { MyNode node = new MyNode(s); if (!node.isNumeric()) { node.right = stk.pop(); node.left = stk.pop(); } stk.push(node); } return stk.peek(); } }; /** * Your TreeBuilder object will be instantiated and called as such: * TreeBuilder obj = new TreeBuilder(); * Node expTree = obj.buildTree(postfix); * int ans = expTree.evaluate(); */ -
/** * This is the interface for the expression tree Node. * You should not remove it, and you can define some classes to implement it. */ class Node { public: virtual ~Node(){}; virtual int evaluate() const = 0; protected: // define your fields here string val; Node* left; Node* right; }; class MyNode : public Node { public: MyNode(string val) { this->val = val; } MyNode(string val, Node* left, Node* right) { this->val = val; this->left = left; this->right = right; } int evaluate() const { if (!(val == "+" || val == "-" || val == "*" || val == "/")) return stoi(val); auto leftVal = left->evaluate(), rightVal = right->evaluate(); if (val == "+") return leftVal + rightVal; if (val == "-") return leftVal - rightVal; if (val == "*") return leftVal * rightVal; if (val == "/") return leftVal / rightVal; return 0; } }; /** * This is the TreeBuilder class. * You can treat it as the driver code that takes the postinfix input * and returns the expression tree represnting it as a Node. */ class TreeBuilder { public: Node* buildTree(vector<string>& postfix) { stack<MyNode*> stk; for (auto s : postfix) { MyNode* node; if (s == "+" || s == "-" || s == "*" || s == "/") { auto right = stk.top(); stk.pop(); auto left = stk.top(); stk.pop(); node = new MyNode(s, left, right); } else { node = new MyNode(s); } stk.push(node); } return stk.top(); } }; /** * Your TreeBuilder object will be instantiated and called as such: * TreeBuilder* obj = new TreeBuilder(); * Node* expTree = obj->buildTree(postfix); * int ans = expTree->evaluate(); */ -
''' >>> "123".isdigit() True >>> "123abc".isdigit() False ''' """ This is the interface for the expression tree Node. You should not remove it, and you can define some classes to implement it. """ import abc from abc import ABC, abstractmethod class Node(ABC): @abstractmethod # define your fields here def evaluate(self) -> int: pass class MyNode(Node): def __init__(self, val): self.val = val self.left = None self.right = None def evaluate(self) -> int: x = self.val if x.isdigit(): return int(x) left, right = self.left.evaluate(), self.right.evaluate() if x == '+': return left + right if x == '-': return left - right if x == '*': return left * right if x == '/': return left // right """ This is the TreeBuilder class. You can treat it as the driver code that takes the postinfix input and returns the expression tree represnting it as a Node. """ class TreeBuilder(object): def buildTree(self, postfix: List[str]) -> 'Node': stk = [] for s in postfix: node = MyNode(s) if not s.isdigit(): node.right = stk.pop() # post-order, so right-child first node.left = stk.pop() stk.append(node) return stk[-1] """ Your TreeBuilder object will be instantiated and called as such: obj = TreeBuilder(); expTree = obj.buildTree(postfix); ans = expTree.evaluate(); """