Question

Formatted question description: https://leetcode.ca/all/1597.html

A binary expression tree is a kind of binary tree used to represent arithmetic expressions. Each node of a binary expression tree has either zero or two children. Leaf nodes (nodes with 0 children) correspond to operands (numbers), and internal nodes (nodes with 2 children) correspond to the operators '+' (addition), '-' (subtraction), '*' (multiplication), and '/' (division).

For each internal node with operator o, the infix expression it represents is (A o B), where A is the expression the left subtree represents and B is the expression the right subtree represents.

You are given a string s, an infix expression containing operands, the operators described above, and parentheses '(' and ')'.

Return any valid binary expression tree, whose in-order traversal reproduces s after omitting the parenthesis from it.

Please note that order of operations applies in s. That is, expressions in parentheses are evaluated first, and multiplication and division happen before addition and subtraction.

Operands must also appear in the same order in both s and the in-order traversal of the tree.

Example 1:

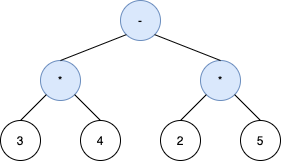
Input: s = "3*4-2*5"
Output: [-,*,*,3,4,2,5]
Explanation: The tree above is the only valid tree whose inorder traversal produces s.

Example 2:

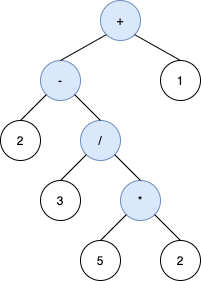
Input: s = "2-3/(5*2)+1"
Output: [+,-,1,2,/,null,null,null,null,3,*,null,null,5,2]
Explanation: The inorder traversal of the tree above is 2-3/5*2+1 which is the same as s without the parenthesis. The tree also produces the correct result and its operands are in the same order as they appear in s.
The tree below is also a valid binary expression tree with the same inorder traversal as s, but it not a valid answer because it does not evaluate to the same value.

The third tree below is also not valid. Although it produces the same result and is equivalent to the above trees, its inorder traversal does not produce s and its operands are not in the same order as s.

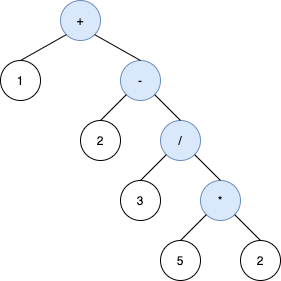
Example 3:

Input: s = "1+2+3+4+5"
Output: [+,+,5,+,4,null,null,+,3,null,null,1,2]
Explanation: The tree [+,+,5,+,+,null,null,1,2,3,4] is also one of many other valid trees.

Constraints:

1 <= s.length <= 100
s consists of digits and the characters '+', '-', '*', and '/'.
Operands in s are exactly 1 digit.
It is guaranteed that s is a valid expression.

Algorithm

To parse an arithmetic expression and construct a binary expression tree, you can follow these steps:

Define Operator Priorities:
- Assign priorities to each operator: consider the left parenthesis as having a priority of 1, addition and subtraction as 2, and multiplication and division as 3.
Manage Stacks for Symbols and Nodes:
- Use a symbol stack where operators are arranged with increasing priority from bottom to top. Also, maintain a Node stack to store the nodes of the expression tree.
Traverse the Expression s:
- Left Parenthesis: Upon encountering a left parenthesis, push it onto the symbol stack.
- Number: When a number is encountered, create a new leaf node and push it onto the Node stack.
- Right Parenthesis: If a right parenthesis is encountered, check the symbol stack’s top for a left parenthesis. If you find a different operator, perform the following:
  - Pop two nodes from the Node stack, assigning them as right and left children (note: the right child is popped first).
  - Pop an operator from the symbol stack to use as the tree’s root.
  - Connect the children to the root, and then push the root onto the Node stack.
  - Continue this process until a left parenthesis is found and popped.
- Operator Encounter: If you encounter an operator, compare its priority with that of the operator at the top of the symbol stack. If the stack’s operator has higher or equal priority:
  - Pop two nodes for the children and an operator for the root as described above, then connect and push back the root.
Finalize the Tree:
- If the Node stack has more than one node, continue the pop and connect operations until only one node remains, which will be the tree root.

The remaining node in the Node stack is the root of the expression tree.

Code

public class Build_Binary_Expression_Tree_From_Infix_Expression {

    public class Solution {

        Map<Character, Integer> prio = new HashMap<>();

        public Node expTree(String s) {

            prio.put('(', 1);
            prio.put('+', 2);
            prio.put('-', 2);
            prio.put('*', 3);
            prio.put('/', 3);

            Deque<Character> ops = new ArrayDeque<>();
            Deque<Node> stack = new ArrayDeque<>();

            for (int i = 0; i < s.length(); i++) {
                char ch = s.charAt(i);
                if (ch == '(') {
                    ops.push(ch);
                } else if (Character.isDigit(ch)) {
                    stack.push(new Node(ch));
                } else if (ch == ')') {
                    while (ops.peek() != '(') {
                        combine(ops, stack);
                    }
                    // pop left '('
                    ops.pop();
                } else {
                    // @note: must be >=, for test case "1+2+3+4+5"
                    while (!ops.isEmpty() && prio.get(ops.peek()) >= prio.get(ch)) {
                        combine(ops, stack);
                    }

                    ops.push(ch);
                }
            }

            while (stack.size() > 1) {
                combine(ops, stack);
            }

            return stack.peek();
        }

        private void combine(Deque<Character> ops, Deque<Node> stack) {
            Node root = new Node(ops.pop());
            // right first, then left
            root.right = stack.pop();
            root.left = stack.pop();

            stack.push(root);
        }
    }

    class Node {
        char val;
        Node left, right;

        public Node(char val) {
            this.val = val;
        }
    }
}

class Solution {
 public:
  Node* expTree(string s) {
    stack<Node*> nodes;  // Stores nodes (new Node(val))
    stack<char> ops;     // Stores operators and parentheses

    for (const char c : s)
      if (isdigit(c)) {
        nodes.push(new Node(c));
      } else if (c == '(') {
        ops.push(c);
      } else if (c == ')') {
        while (ops.top() != '(')
          nodes.push(buildNode(pop(ops), pop(nodes), pop(nodes)));
        ops.pop();  // Remove '('
      } else if (c == '+' || c == '-' || c == '*' || c == '/') {
        while (!ops.empty() && compare(ops.top(), c))
          nodes.push(buildNode(pop(ops), pop(nodes), pop(nodes)));
        ops.push(c);
      }

    while (!ops.empty())
      nodes.push(buildNode(pop(ops), pop(nodes), pop(nodes)));

    return nodes.top();
  }

 private:
  Node* buildNode(char op, Node* right, Node* left) {
    return new Node(op, left, right);
  }

  // Returns true if op1 is a operator and priority(op1) >= priority(op2)
  bool compare(char op1, char op2) {
    if (op1 == '(' || op1 == ')')
      return false;
    return op1 == '*' || op1 == '/' || op2 == '+' || op2 == '-';
  }

  char pop(stack<char>& ops) {
    const char op = ops.top();
    ops.pop();
    return op;
  }

  Node* pop(stack<Node*>& nodes) {
    Node* node = nodes.top();
    nodes.pop();
    return node;
  }
};

'''
1. 题目信息：数字只有一位数
2. char直接成node。运算符最后combine()再成node
'''
class Solution:

    def __init__(self):
        self.priority = {
            '(': 1,
            '+': 2,
            '-': 2,
            '*': 3,
            '/': 3,
        }

    def expTree(self, s: str) -> 'Node':
        ops = [] # not Node yet
        stack = [] # already Node

        for ch in s:
            if ch == '(':
                ops.append(ch)
            elif ch.isdigit():
                stack.append(Node(ch)) # assumption: only single digit for each node
            elif ch == ')':
                while ops[-1] != '(':
                    self.combine(ops, stack)
                ops.pop() # pop left '('
            else: # then operator
                # @note: must be >=, for test case "1+2+3+4+5"
                while ops and self.priority.get(ops[-1], 0) >= self.priority[ch]:
                    self.combine(ops, stack)

                ops.append(ch)

        while len(stack) > 1: # eg input, '1+2'
            self.combine(ops, stack)

        return stack[0]

    def combine(self, ops: list, stack: list) -> None:
        root = Node(ops.pop())
        # right first, then left, since it's a stack
        root.right = stack.pop()
        root.left = stack.pop()

        stack.append(root)


class Node:

    def __init__(self, val: str):
        self.val = val
        self.left = None
        self.right = None

################

'''
The solution uses two main functions: buildTree and infixToPostfix.
* The buildTree function takes an infix expression as input, converts it to postfix using the infixToPostfix function, and then builds the binary expression tree using a stack.
* The infixToPostfix function converts the infix expression to postfix using the shunting yard algorithm.

The TreeNode class is defined to represent nodes in the binary expression tree. Each node has a value, left child, and right child. The precedence dictionary is used to determine the precedence of operators in the expression.

'''
class TreeNode:
    def __init__(self, val='', left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

class Solution:
    def __init__(self):
        self.precedence = {'+': 1, '-': 1, '*': 2, '/': 2}

    def buildTree(self, expression: str) -> TreeNode:
        postfix = self.infixToPostfix(expression)
        stack = []
        for char in postfix:
            if char.isdigit():
                node = TreeNode(char)
                stack.append(node)
            else:
                right = stack.pop()
                left = stack.pop()
                node = TreeNode(char, left, right)
                stack.append(node)
        return stack.pop()

    # converts infix to postfix
    def infixToPostfix(self, expression):
        postfix = []
        operator_stack = []
        i = 0
        while i < len(expression):
            if expression[i].isdigit():
                j = i
                while j < len(expression) and expression[j].isdigit():
                    j += 1
                postfix.append(expression[i:j])
                i = j
            elif expression[i] in self.precedence:
                while operator_stack and operator_stack[-1] != '(' and self.precedence[operator_stack[-1]] >= self.precedence[expression[i]]:
                    postfix.append(operator_stack.pop())
                operator_stack.append(expression[i])
                i += 1
            elif expression[i] == '(':
                operator_stack.append(expression[i])
                i += 1
            elif expression[i] == ')':
                while operator_stack and operator_stack[-1] != '(':
                    postfix.append(operator_stack.pop())
                operator_stack.pop()
                i += 1
            else:
                i += 1
        while operator_stack:
            postfix.append(operator_stack.pop())
        return postfix

1597 - Build Binary Expression Tree From Infix Expression

Question

Algorithm

Code

All Problems

All Solutions

Welcome to Subscribe On Youtube

Question

Algorithm

Code

All Problems

All Solutions