Welcome to Subscribe On Youtube

1582. Special Positions in a Binary Matrix

Description

Given an m x n binary matrix mat, return the number of special positions in mat.

A position (i, j) is called special if mat[i][j] == 1 and all other elements in row i and column j are 0 (rows and columns are 0-indexed).

 

Example 1:

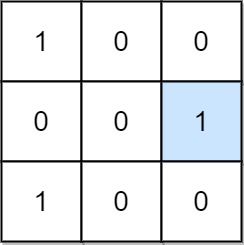
Input: mat = [[1,0,0],[0,0,1],[1,0,0]]
Output: 1
Explanation: (1, 2) is a special position because mat[1][2] == 1 and all other elements in row 1 and column 2 are 0.

Example 2:

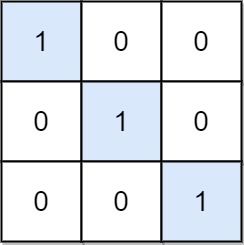
Input: mat = [[1,0,0],[0,1,0],[0,0,1]]
Output: 3
Explanation: (0, 0), (1, 1) and (2, 2) are special positions.

 

Constraints:

  • m == mat.length
  • n == mat[i].length
  • 1 <= m, n <= 100
  • mat[i][j] is either 0 or 1.

Solutions

  • class Solution {
    public int numSpecial(int[][] mat) {
        int m = mat.length, n = mat[0].length;
        int[] r = new int[m];
        int[] c = new int[n];
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                r[i] += mat[i][j];
                c[j] += mat[i][j];
            }
        }
        int ans = 0;
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (mat[i][j] == 1 && r[i] == 1 && c[j] == 1) {
                    ++ans;
                }
            }
        }
        return ans;
    }
}

  • class Solution {
public:
    int numSpecial(vector<vector<int>>& mat) {
        int m = mat.size(), n = mat[0].size();
        vector<int> r(m), c(n);
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                r[i] += mat[i][j];
                c[j] += mat[i][j];
            }
        }
        int ans = 0;
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (mat[i][j] == 1 && r[i] == 1 && c[j] == 1) {
                    ++ans;
                }
            }
        }
        return ans;
    }
};

  • class Solution:
    def numSpecial(self, mat: List[List[int]]) -> int:
        m, n = len(mat), len(mat[0])
        r = [0] * m
        c = [0] * n
        for i, row in enumerate(mat):
            for j, v in enumerate(row):
                r[i] += v
                c[j] += v
        ans = 0
        for i in range(m):
            for j in range(n):
                if mat[i][j] == 1 and r[i] == 1 and c[j] == 1:
                    ans += 1
        return ans


  • func numSpecial(mat [][]int) int {
	m, n := len(mat), len(mat[0])
	r, c := make([]int, m), make([]int, n)
	for i, row := range mat {
		for j, v := range row {
			r[i] += v
			c[j] += v
		}
	}
	ans := 0
	for i, x := range r {
		for j, y := range c {
			if mat[i][j] == 1 && x == 1 && y == 1 {
				ans++
			}
		}
	}
	return ans
}

  • function numSpecial(mat: number[][]): number {
    const m = mat.length;
    const n = mat[0].length;
    const rows = new Array(m).fill(0);
    const cols = new Array(n).fill(0);
    for (let i = 0; i < m; i++) {
        for (let j = 0; j < n; j++) {
            if (mat[i][j] === 1) {
                rows[i]++;
                cols[j]++;
            }
        }
    }

    let res = 0;
    for (let i = 0; i < m; i++) {
        for (let j = 0; j < n; j++) {
            if (mat[i][j] === 1 && rows[i] === 1 && cols[j] === 1) {
                res++;
            }
        }
    }

    return res;
}


  • impl Solution {
    pub fn num_special(mat: Vec<Vec<i32>>) -> i32 {
        let m = mat.len();
        let n = mat[0].len();
        let mut rows = vec![0; m];
        let mut cols = vec![0; n];
        for i in 0..m {
            for j in 0..n {
                rows[i] += mat[i][j];
                cols[j] += mat[i][j];
            }
        }

        let mut res = 0;
        for i in 0..m {
            for j in 0..n {
                if mat[i][j] == 1 && rows[i] == 1 && cols[j] == 1 {
                    res += 1;
                }
            }
        }
        res
    }
}

All Problems

All Solutions