Welcome to Subscribe On Youtube
1368. Minimum Cost to Make at Least One Valid Path in a Grid
Description
Given an m x n grid. Each cell of the grid has a sign pointing to the next cell you should visit if you are currently in this cell. The sign of grid[i][j] can be:
1which means go to the cell to the right. (i.e go fromgrid[i][j]togrid[i][j + 1])2which means go to the cell to the left. (i.e go fromgrid[i][j]togrid[i][j - 1])3which means go to the lower cell. (i.e go fromgrid[i][j]togrid[i + 1][j])4which means go to the upper cell. (i.e go fromgrid[i][j]togrid[i - 1][j])
Notice that there could be some signs on the cells of the grid that point outside the grid.
You will initially start at the upper left cell (0, 0). A valid path in the grid is a path that starts from the upper left cell (0, 0) and ends at the bottom-right cell (m - 1, n - 1) following the signs on the grid. The valid path does not have to be the shortest.
You can modify the sign on a cell with cost = 1. You can modify the sign on a cell one time only.
Return the minimum cost to make the grid have at least one valid path.
Example 1:
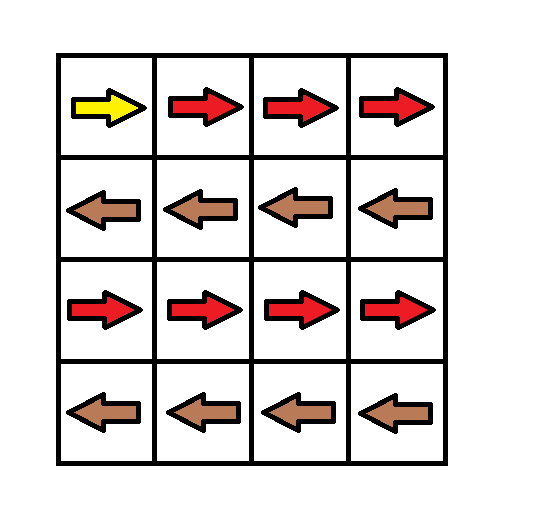
Input: grid = [[1,1,1,1],[2,2,2,2],[1,1,1,1],[2,2,2,2]] Output: 3 Explanation: You will start at point (0, 0). The path to (3, 3) is as follows. (0, 0) --> (0, 1) --> (0, 2) --> (0, 3) change the arrow to down with cost = 1 --> (1, 3) --> (1, 2) --> (1, 1) --> (1, 0) change the arrow to down with cost = 1 --> (2, 0) --> (2, 1) --> (2, 2) --> (2, 3) change the arrow to down with cost = 1 --> (3, 3) The total cost = 3.
Example 2:
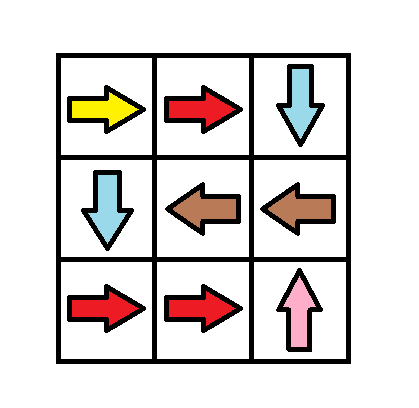
Input: grid = [[1,1,3],[3,2,2],[1,1,4]] Output: 0 Explanation: You can follow the path from (0, 0) to (2, 2).
Example 3:
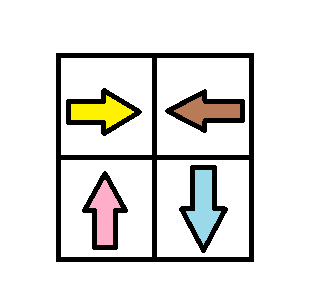
Input: grid = [[1,2],[4,3]] Output: 1
Constraints:
m == grid.lengthn == grid[i].length1 <= m, n <= 1001 <= grid[i][j] <= 4
Solutions
Solution 1: Double-ended Queue BFS
This problem is essentially a shortest path model, but what we are looking for is the minimum number of direction changes.
In an undirected graph where the edge weights are only 0 and 1, we can use a double-ended queue for BFS. The principle is that when the weight of the point that can be expanded currently is 0, it is added to the front of the queue; when the weight is 1, it is added to the end of the queue.
If the weight of an edge is 0, then the weight of the newly expanded node is the same as the weight of the current queue head node. Obviously, it can be used as the starting point for the next expansion.
-
class Solution { public int minCost(int[][] grid) { int m = grid.length, n = grid[0].length; boolean[][] vis = new boolean[m][n]; Deque<int[]> q = new ArrayDeque<>(); q.offer(new int[] {0, 0, 0}); int[][] dirs = { {0, 0}, {0, 1}, {0, -1}, {1, 0}, {-1, 0} }; while (!q.isEmpty()) { int[] p = q.poll(); int i = p[0], j = p[1], d = p[2]; if (i == m - 1 && j == n - 1) { return d; } if (vis[i][j]) { continue; } vis[i][j] = true; for (int k = 1; k <= 4; ++k) { int x = i + dirs[k][0], y = j + dirs[k][1]; if (x >= 0 && x < m && y >= 0 && y < n) { if (grid[i][j] == k) { q.offerFirst(new int[] {x, y, d}); } else { q.offer(new int[] {x, y, d + 1}); } } } } return -1; } } -
class Solution { public: int minCost(vector<vector<int>>& grid) { int m = grid.size(), n = grid[0].size(); vector<vector<bool>> vis(m, vector<bool>(n)); vector<vector<int>> dirs = { {0, 0}, {0, 1}, {0, -1}, {1, 0}, {-1, 0} }; deque<pair<int, int>> q; q.push_back({0, 0}); while (!q.empty()) { auto p = q.front(); q.pop_front(); int i = p.first / n, j = p.first % n, d = p.second; if (i == m - 1 && j == n - 1) return d; if (vis[i][j]) continue; vis[i][j] = true; for (int k = 1; k <= 4; ++k) { int x = i + dirs[k][0], y = j + dirs[k][1]; if (x >= 0 && x < m && y >= 0 && y < n) { if (grid[i][j] == k) q.push_front({x * n + y, d}); else q.push_back({x * n + y, d + 1}); } } } return -1; } }; -
class Solution: def minCost(self, grid: List[List[int]]) -> int: m, n = len(grid), len(grid[0]) dirs = [[0, 0], [0, 1], [0, -1], [1, 0], [-1, 0]] q = deque([(0, 0, 0)]) vis = set() while q: i, j, d = q.popleft() if (i, j) in vis: continue vis.add((i, j)) if i == m - 1 and j == n - 1: return d for k in range(1, 5): x, y = i + dirs[k][0], j + dirs[k][1] if 0 <= x < m and 0 <= y < n: if grid[i][j] == k: q.appendleft((x, y, d)) else: q.append((x, y, d + 1)) return -1 -
func minCost(grid [][]int) int { m, n := len(grid), len(grid[0]) q := doublylinkedlist.New() q.Add([]int{0, 0, 0}) dirs := [][]int{ {0, 0}, {0, 1}, {0, -1}, {1, 0}, {-1, 0} } vis := make([][]bool, m) for i := range vis { vis[i] = make([]bool, n) } for !q.Empty() { v, _ := q.Get(0) p := v.([]int) q.Remove(0) i, j, d := p[0], p[1], p[2] if i == m-1 && j == n-1 { return d } if vis[i][j] { continue } vis[i][j] = true for k := 1; k <= 4; k++ { x, y := i+dirs[k][0], j+dirs[k][1] if x >= 0 && x < m && y >= 0 && y < n { if grid[i][j] == k { q.Insert(0, []int{x, y, d}) } else { q.Add([]int{x, y, d + 1}) } } } } return -1 } -
function minCost(grid: number[][]): number { const m = grid.length, n = grid[0].length; let ans = Array.from({ length: m }, v => new Array(n).fill(Infinity)); ans[0][0] = 0; let queue = [[0, 0]]; const dirs = [ [0, 1], [0, -1], [1, 0], [-1, 0], ]; while (queue.length) { let [x, y] = queue.shift(); for (let step = 1; step < 5; step++) { let [dx, dy] = dirs[step - 1]; let [i, j] = [x + dx, y + dy]; if (i < 0 || i >= m || j < 0 || j >= n) continue; let cost = ~~(grid[x][y] != step) + ans[x][y]; if (cost >= ans[i][j]) continue; ans[i][j] = cost; if (grid[x][y] == step) { queue.unshift([i, j]); } else { queue.push([i, j]); } } } return ans[m - 1][n - 1]; }