Welcome to Subscribe On Youtube

1292. Maximum Side Length of a Square with Sum Less than or Equal to Threshold

Description

Given a m x n matrix mat and an integer threshold, return the maximum side-length of a square with a sum less than or equal to threshold or return 0 if there is no such square.

 

Example 1:

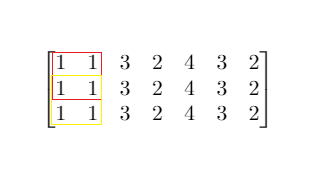
Input: mat = [[1,1,3,2,4,3,2],[1,1,3,2,4,3,2],[1,1,3,2,4,3,2]], threshold = 4
Output: 2
Explanation: The maximum side length of square with sum less than 4 is 2 as shown.

Example 2:

Input: mat = [[2,2,2,2,2],[2,2,2,2,2],[2,2,2,2,2],[2,2,2,2,2],[2,2,2,2,2]], threshold = 1
Output: 0

 

Constraints:

• m == mat.length
• n == mat[i].length
• 1 <= m, n <= 300
• 0 <= mat[i][j] <= 104
• 0 <= threshold <= 105

Solutions

• Java
• C++
• Python
• Go
• TypeScript

• class Solution {
      private int m;
      private int n;
      private int threshold;
      private int[][] s;
  
      public int maxSideLength(int[][] mat, int threshold) {
          m = mat.length;
          n = mat[0].length;
          this.threshold = threshold;
          s = new int[m + 1][n + 1];
          for (int i = 1; i <= m; ++i) {
              for (int j = 1; j <= n; ++j) {
                  s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + mat[i - 1][j - 1];
              }
          }
          int l = 0, r = Math.min(m, n);
          while (l < r) {
              int mid = (l + r + 1) >> 1;
              if (check(mid)) {
                  l = mid;
              } else {
                  r = mid - 1;
              }
          }
          return l;
      }
  
      private boolean check(int k) {
          for (int i = 0; i < m - k + 1; ++i) {
              for (int j = 0; j < n - k + 1; ++j) {
                  if (s[i + k][j + k] - s[i][j + k] - s[i + k][j] + s[i][j] <= threshold) {
                      return true;
                  }
              }
          }
          return false;
      }
  }
  

• class Solution {
  public:
      int maxSideLength(vector<vector<int>>& mat, int threshold) {
          int m = mat.size(), n = mat[0].size();
          int s[m + 1][n + 1];
          memset(s, 0, sizeof(s));
          for (int i = 1; i <= m; ++i) {
              for (int j = 1; j <= n; ++j) {
                  s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + mat[i - 1][j - 1];
              }
          }
          auto check = [&](int k) {
              for (int i = 0; i < m - k + 1; ++i) {
                  for (int j = 0; j < n - k + 1; ++j) {
                      if (s[i + k][j + k] - s[i][j + k] - s[i + k][j] + s[i][j] <= threshold) {
                          return true;
                      }
                  }
              }
              return false;
          };
          int l = 0, r = min(m, n);
          while (l < r) {
              int mid = (l + r + 1) >> 1;
              if (check(mid)) {
                  l = mid;
              } else {
                  r = mid - 1;
              }
          }
          return l;
      }
  };
  

• class Solution:
      def maxSideLength(self, mat: List[List[int]], threshold: int) -> int:
          def check(k: int) -> bool:
              for i in range(m - k + 1):
                  for j in range(n - k + 1):
                      v = s[i + k][j + k] - s[i][j + k] - s[i + k][j] + s[i][j]
                      if v <= threshold:
                          return True
              return False
  
          m, n = len(mat), len(mat[0])
          s = [[0] * (n + 1) for _ in range(m + 1)]
          for i, row in enumerate(mat, 1):
              for j, x in enumerate(row, 1):
                  s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + x
          l, r = 0, min(m, n)
          while l < r:
              mid = (l + r + 1) >> 1
              if check(mid):
                  l = mid
              else:
                  r = mid - 1
          return l
  
  

• func maxSideLength(mat [][]int, threshold int) int {
  	m, n := len(mat), len(mat[0])
  	s := make([][]int, m+1)
  	for i := range s {
  		s[i] = make([]int, n+1)
  	}
  	for i := 1; i <= m; i++ {
  		for j := 1; j <= n; j++ {
  			s[i][j] = s[i-1][j] + s[i][j-1] - s[i-1][j-1] + mat[i-1][j-1]
  		}
  	}
  	check := func(k int) bool {
  		for i := 0; i < m-k+1; i++ {
  			for j := 0; j < n-k+1; j++ {
  				if s[i+k][j+k]-s[i][j+k]-s[i+k][j]+s[i][j] <= threshold {
  					return true
  				}
  			}
  		}
  		return false
  	}
  	l, r := 0, min(m, n)
  	for l < r {
  		mid := (l + r + 1) >> 1
  		if check(mid) {
  			l = mid
  		} else {
  			r = mid - 1
  		}
  	}
  	return l
  }
  

• function maxSideLength(mat: number[][], threshold: number): number {
      const m = mat.length;
      const n = mat[0].length;
      const s: number[][] = Array(m + 1)
          .fill(0)
          .map(() => Array(n + 1).fill(0));
      for (let i = 1; i <= m; ++i) {
          for (let j = 1; j <= n; ++j) {
              s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + mat[i - 1][j - 1];
          }
      }
      const check = (k: number): boolean => {
          for (let i = 0; i < m - k + 1; ++i) {
              for (let j = 0; j < n - k + 1; ++j) {
                  if (s[i + k][j + k] - s[i + k][j] - s[i][j + k] + s[i][j] <= threshold) {
                      return true;
                  }
              }
          }
          return false;
      };
  
      let l = 0;
      let r = Math.min(m, n);
      while (l < r) {
          const mid = (l + r + 1) >> 1;
          if (check(mid)) {
              l = mid;
          } else {
              r = mid - 1;
          }
      }
      return l;
  }
  
  

All Problems

All Solutions