Welcome to Subscribe On Youtube
1168. Optimize Water Distribution in a Village
Description
There are n houses in a village. We want to supply water for all the houses by building wells and laying pipes.
For each house i, we can either build a well inside it directly with cost wells[i - 1] (note the -1 due to 0-indexing), or pipe in water from another well to it. The costs to lay pipes between houses are given by the array pipes where each pipes[j] = [house1j, house2j, costj] represents the cost to connect house1j and house2j together using a pipe. Connections are bidirectional, and there could be multiple valid connections between the same two houses with different costs.
Return the minimum total cost to supply water to all houses.
Example 1:
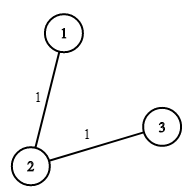
Input: n = 3, wells = [1,2,2], pipes = [[1,2,1],[2,3,1]] Output: 3 Explanation: The image shows the costs of connecting houses using pipes. The best strategy is to build a well in the first house with cost 1 and connect the other houses to it with cost 2 so the total cost is 3.
Example 2:
Input: n = 2, wells = [1,1], pipes = [[1,2,1],[1,2,2]] Output: 2 Explanation: We can supply water with cost two using one of the three options: Option 1: - Build a well inside house 1 with cost 1. - Build a well inside house 2 with cost 1. The total cost will be 2. Option 2: - Build a well inside house 1 with cost 1. - Connect house 2 with house 1 with cost 1. The total cost will be 2. Option 3: - Build a well inside house 2 with cost 1. - Connect house 1 with house 2 with cost 1. The total cost will be 2. Note that we can connect houses 1 and 2 with cost 1 or with cost 2 but we will always choose the cheapest option.
Constraints:
2 <= n <= 104wells.length == n0 <= wells[i] <= 1051 <= pipes.length <= 104pipes[j].length == 31 <= house1j, house2j <= n0 <= costj <= 105house1j != house2j
Solutions
Solution 1: Kruskal’s Algorithm (Minimum Spanning Tree)
We assume that there is a well with the number $0$. Then we can consider the connectivity between each house and the well $0$ as an edge, and the weight of each edge is the cost of building a well for that house. At the same time, we consider the connectivity between each house as an edge, and the weight of each edge is the cost of laying a pipe. In this way, we can transform this problem into finding the minimum spanning tree of an undirected graph.
We can use Kruskal’s algorithm to find the minimum spanning tree of the undirected graph. First, we add an edge between the well $0$ and the house to the $pipes$ array, and then sort the $pipes$ array in ascending order of edge weights. Then, we traverse each edge. If this edge connects different connected components, we choose this edge and merge the corresponding connected components. If the current connected component is exactly $1$, then we have found the minimum spanning tree. The answer at this time is the current edge weight, and we return it.
The time complexity is $O((m + n) \times \log (m + n))$, and the space complexity is $O(m + n)$. Here, $m$ and $n$ are the lengths of the $pipes$ array and the $wells$ array, respectively.
-
class Solution { private int[] p; public int minCostToSupplyWater(int n, int[] wells, int[][] pipes) { int[][] nums = Arrays.copyOf(pipes, pipes.length + n); for (int i = 0; i < n; i++) { nums[pipes.length + i] = new int[] {0, i + 1, wells[i]}; } Arrays.sort(nums, (a, b) -> a[2] - b[2]); p = new int[n + 1]; for (int i = 0; i <= n; i++) { p[i] = i; } int ans = 0; for (var x : nums) { int a = x[0], b = x[1], c = x[2]; int pa = find(a), pb = find(b); if (pa != pb) { p[pa] = pb; ans += c; if (--n == 0) { return ans; } } } return ans; } private int find(int x) { if (p[x] != x) { p[x] = find(p[x]); } return p[x]; } } -
class Solution { public: int minCostToSupplyWater(int n, vector<int>& wells, vector<vector<int>>& pipes) { for (int i = 0; i < n; ++i) { pipes.push_back({0, i + 1, wells[i]}); } sort(pipes.begin(), pipes.end(), [](const vector<int>& a, const vector<int>& b) { return a[2] < b[2]; }); int p[n + 1]; iota(p, p + n + 1, 0); function<int(int)> find = [&](int x) { if (p[x] != x) { p[x] = find(p[x]); } return p[x]; }; int ans = 0; for (const auto& x : pipes) { int pa = find(x[0]), pb = find(x[1]); if (pa == pb) { continue; } p[pa] = pb; ans += x[2]; if (--n == 0) { break; } } return ans; } }; -
class Solution: def minCostToSupplyWater( self, n: int, wells: List[int], pipes: List[List[int]] ) -> int: def find(x: int) -> int: if p[x] != x: p[x] = find(p[x]) return p[x] for i, w in enumerate(wells, 1): pipes.append([0, i, w]) pipes.sort(key=lambda x: x[2]) p = list(range(n + 1)) ans = 0 for a, b, c in pipes: pa, pb = find(a), find(b) if pa != pb: p[pa] = pb n -= 1 ans += c if n == 0: return ans -
func minCostToSupplyWater(n int, wells []int, pipes [][]int) (ans int) { for i, w := range wells { pipes = append(pipes, []int{0, i + 1, w}) } sort.Slice(pipes, func(i, j int) bool { return pipes[i][2] < pipes[j][2] }) p := make([]int, n+1) for i := range p { p[i] = i } var find func(int) int find = func(x int) int { if p[x] != x { p[x] = find(p[x]) } return p[x] } for _, x := range pipes { pa, pb := find(x[0]), find(x[1]) if pa == pb { continue } p[pa] = pb ans += x[2] n-- if n == 0 { break } } return } -
function minCostToSupplyWater(n: number, wells: number[], pipes: number[][]): number { for (let i = 0; i < n; ++i) { pipes.push([0, i + 1, wells[i]]); } pipes.sort((a, b) => a[2] - b[2]); const p = Array(n + 1) .fill(0) .map((_, i) => i); const find = (x: number): number => { if (p[x] !== x) { p[x] = find(p[x]); } return p[x]; }; let ans = 0; for (const [a, b, c] of pipes) { const pa = find(a); const pb = find(b); if (pa === pb) { continue; } p[pa] = pb; ans += c; if (--n === 0) { break; } } return ans; } -
struct UnionFind { p: Vec<usize>, size: Vec<usize>, } impl UnionFind { fn new(n: usize) -> Self { let p: Vec<usize> = (0..n).collect(); let size = vec![1; n]; UnionFind { p, size } } fn find(&mut self, x: usize) -> usize { if self.p[x] != x { self.p[x] = self.find(self.p[x]); } self.p[x] } fn union(&mut self, a: usize, b: usize) -> bool { let pa = self.find(a); let pb = self.find(b); if pa == pb { false } else if self.size[pa] > self.size[pb] { self.p[pb] = pa; self.size[pa] += self.size[pb]; true } else { self.p[pa] = pb; self.size[pb] += self.size[pa]; true } } } impl Solution { pub fn min_cost_to_supply_water(n: i32, wells: Vec<i32>, pipes: Vec<Vec<i32>>) -> i32 { let n = n as usize; let mut pipes = pipes; for i in 0..n { pipes.push(vec![0, (i + 1) as i32, wells[i]]); } pipes.sort_by(|a, b| a[2].cmp(&b[2])); let mut uf = UnionFind::new(n + 1); let mut ans = 0; for pipe in pipes { let a = pipe[0] as usize; let b = pipe[1] as usize; let c = pipe[2]; if uf.union(a, b) { ans += c; if n == 0 { break; } } } ans } }