Welcome to Subscribe On Youtube

1135. Connecting Cities With Minimum Cost

Description

There are n cities labeled from 1 to n. You are given the integer n and an array connections where connections[i] = [xi, yi, costi] indicates that the cost of connecting city xi and city yi (bidirectional connection) is costi.

Return the minimum cost to connect all the n cities such that there is at least one path between each pair of cities. If it is impossible to connect all the n cities, return -1,

The cost is the sum of the connections' costs used.

 

Example 1:

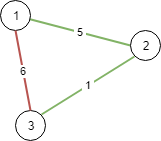
Input: n = 3, connections = [[1,2,5],[1,3,6],[2,3,1]]
Output: 6
Explanation: Choosing any 2 edges will connect all cities so we choose the minimum 2.

Example 2:

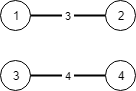
Input: n = 4, connections = [[1,2,3],[3,4,4]]
Output: -1
Explanation: There is no way to connect all cities even if all edges are used.

 

Constraints:

• 1 <= n <= 104
• 1 <= connections.length <= 104
• connections[i].length == 3
• 1 <= xi, yi <= n
• xi != yi
• 0 <= costi <= 105

Solutions

Solution 1: Kruskal’s Algorithm

Kruskal’s algorithm is a greedy algorithm used to compute the minimum spanning tree.

The basic idea of Kruskal’s algorithm is to select the smallest edge from the edge set each time.

• If the two vertices connected by this edge are not in the same connected component, then add this edge to the minimum spanning tree,
• otherwise discard this edge.

For this problem, we can sort the edges in ascending order of connection cost, use a union-find set to maintain connected components, select the smallest edge each time, and

• if the two vertices connected by this edge are not in the same connected component, then merge these two vertices and accumulate the connection cost.
• If a situation occurs where the number of connected components is $1$, it means that all vertices are connected, and we return the accumulated connection cost, otherwise, we return $-1$.

The time complexity is $O(m \times \log m)$, and the space complexity is $O(n)$. Here, $m$ and $n$ are the number of edges and vertices, respectively.

• Java
• C++
• Python
• Go
• TypeScript

• class Solution {
      private int[] p;
  
      public int minimumCost(int n, int[][] connections) {
          Arrays.sort(connections, Comparator.comparingInt(a -> a[2]));
          p = new int[n];
          for (int i = 0; i < n; ++i) {
              p[i] = i;
          }
          int ans = 0;
          for (int[] e : connections) {
              int x = e[0] - 1, y = e[1] - 1, cost = e[2];
              if (find(x) == find(y)) {
                  continue;
              }
              p[find(x)] = find(y);
              ans += cost;
              if (--n == 1) {
                  return ans;
              }
          }
          return -1;
      }
  
      private int find(int x) {
          if (p[x] != x) {
              p[x] = find(p[x]);
          }
          return p[x];
      }
  }
  

• class Solution {
  public:
      int minimumCost(int n, vector<vector<int>>& connections) {
          vector<int> p(n);
          iota(p.begin(), p.end(), 0);
          sort(connections.begin(), connections.end(), [](auto& a, auto& b) { return a[2] < b[2]; });
          int ans = 0;
          function<int(int)> find = [&](int x) -> int {
              if (p[x] != x) {
                  p[x] = find(p[x]);
              }
              return p[x];
          };
          for (auto& e : connections) {
              int x = e[0] - 1, y = e[1] - 1, cost = e[2];
              if (find(x) == find(y)) {
                  continue;
              }
              p[find(x)] = find(y);
              ans += cost;
              if (--n == 1) {
                  return ans;
              }
          }
          return -1;
      }
  };
  

• class Solution:
      def minimumCost(self, n: int, connections: List[List[int]]) -> int:
          def find(x):
              if p[x] != x:
                  p[x] = find(p[x])
              return p[x]
  
          connections.sort(key=lambda x: x[2])
          p = list(range(n))
          ans = 0
          for x, y, cost in connections:
              x, y = x - 1, y - 1
              if find(x) == find(y):
                  continue # already connected with ealier lower cost
              p[find(x)] = find(y)
              ans += cost
              n -= 1
              if n == 1:
                  return ans
          return -1
  
  

• func minimumCost(n int, connections [][]int) (ans int) {
  	p := make([]int, n)
  	for i := range p {
  		p[i] = i
  	}
  	sort.Slice(connections, func(i, j int) bool { return connections[i][2] < connections[j][2] })
  	var find func(int) int
  	find = func(x int) int {
  		if p[x] != x {
  			p[x] = find(p[x])
  		}
  		return p[x]
  	}
  	for _, e := range connections {
  		x, y, cost := e[0]-1, e[1]-1, e[2]
  		if find(x) == find(y) {
  			continue
  		}
  		p[find(x)] = find(y)
  		ans += cost
  		n--
  		if n == 1 {
  			return
  		}
  	}
  	return -1
  }
  

• function minimumCost(n: number, connections: number[][]): number {
      const p = new Array(n);
      for (let i = 0; i < n; ++i) {
          p[i] = i;
      }
      const find = (x: number): number => {
          if (p[x] !== x) {
              p[x] = find(p[x]);
          }
          return p[x];
      };
      connections.sort((a, b) => a[2] - b[2]);
      let ans = 0;
      for (const [x, y, cost] of connections) {
          if (find(x - 1) == find(y - 1)) {
              continue;
          }
          p[find(x - 1)] = find(y - 1);
          ans += cost;
          if (--n == 1) {
              return ans;
          }
      }
      return -1;
  }
  
  

All Problems

All Solutions