Welcome to Subscribe On Youtube
1136. Parallel Courses
Description
You are given an integer n, which indicates that there are n courses labeled from 1 to n. You are also given an array relations where relations[i] = [prevCoursei, nextCoursei], representing a prerequisite relationship between course prevCoursei and course nextCoursei: course prevCoursei has to be taken before course nextCoursei.
In one semester, you can take any number of courses as long as you have taken all the prerequisites in the previous semester for the courses you are taking.
Return the minimum number of semesters needed to take all courses. If there is no way to take all the courses, return -1.
Example 1:
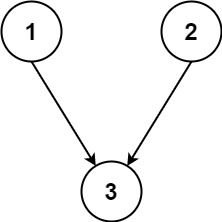
Input: n = 3, relations = [[1,3],[2,3]] Output: 2 Explanation: The figure above represents the given graph. In the first semester, you can take courses 1 and 2. In the second semester, you can take course 3.
Example 2:

Input: n = 3, relations = [[1,2],[2,3],[3,1]] Output: -1 Explanation: No course can be studied because they are prerequisites of each other.
Constraints:
1 <= n <= 50001 <= relations.length <= 5000relations[i].length == 21 <= prevCoursei, nextCoursei <= nprevCoursei != nextCoursei- All the pairs
[prevCoursei, nextCoursei]are unique.
Solutions
Solution 1: Topological Sorting
We can first build a graph $g$ to represent the prerequisite relationships between courses, and count the in-degree $indeg$ of each course.
Then we enqueue the courses with an in-degree of $0$ and start topological sorting. Each time, we dequeue a course from the queue, reduce the in-degree of the courses that it points to by $1$, and if the in-degree becomes $0$ after reduction, we enqueue that course. When the queue is empty, if there are still courses that have not been completed, it means that it is impossible to complete all courses, so we return $-1$. Otherwise, we return the number of semesters required to complete all courses.
The time complexity is $O(n + m)$, and the space complexity is $O(n + m)$. Here, $n$ and $m$ are the number of courses and the number of prerequisite relationships, respectively.
-
class Solution { public int minimumSemesters(int n, int[][] relations) { List<Integer>[] g = new List[n]; Arrays.setAll(g, k -> new ArrayList<>()); int[] indeg = new int[n]; for (var r : relations) { int prev = r[0] - 1, nxt = r[1] - 1; g[prev].add(nxt); ++indeg[nxt]; } Deque<Integer> q = new ArrayDeque<>(); for (int i = 0; i < n; ++i) { if (indeg[i] == 0) { q.offer(i); } } int ans = 0; while (!q.isEmpty()) { ++ans; for (int k = q.size(); k > 0; --k) { int i = q.poll(); --n; for (int j : g[i]) { if (--indeg[j] == 0) { q.offer(j); } } } } return n == 0 ? ans : -1; } } -
class Solution { public: int minimumSemesters(int n, vector<vector<int>>& relations) { vector<vector<int>> g(n); vector<int> indeg(n); for (auto& r : relations) { int prev = r[0] - 1, nxt = r[1] - 1; g[prev].push_back(nxt); ++indeg[nxt]; } queue<int> q; for (int i = 0; i < n; ++i) { if (indeg[i] == 0) { q.push(i); } } int ans = 0; while (!q.empty()) { ++ans; for (int k = q.size(); k; --k) { int i = q.front(); q.pop(); --n; for (int& j : g[i]) { if (--indeg[j] == 0) { q.push(j); } } } } return n == 0 ? ans : -1; } }; -
class Solution: def minimumSemesters(self, n: int, relations: List[List[int]]) -> int: g = defaultdict(list) indeg = [0] * n for prev, nxt in relations: prev, nxt = prev - 1, nxt - 1 g[prev].append(nxt) indeg[nxt] += 1 q = deque(i for i, v in enumerate(indeg) if v == 0) ans = 0 while q: ans += 1 for _ in range(len(q)): i = q.popleft() n -= 1 for j in g[i]: indeg[j] -= 1 if indeg[j] == 0: q.append(j) return -1 if n else ans -
func minimumSemesters(n int, relations [][]int) (ans int) { g := make([][]int, n) indeg := make([]int, n) for _, r := range relations { prev, nxt := r[0]-1, r[1]-1 g[prev] = append(g[prev], nxt) indeg[nxt]++ } q := []int{} for i, v := range indeg { if v == 0 { q = append(q, i) } } for len(q) > 0 { ans++ for k := len(q); k > 0; k-- { i := q[0] q = q[1:] n-- for _, j := range g[i] { indeg[j]-- if indeg[j] == 0 { q = append(q, j) } } } } if n == 0 { return } return -1 } -
function minimumSemesters(n: number, relations: number[][]): number { const g = Array.from({ length: n }, () => []); const indeg = new Array(n).fill(0); for (const [prev, nxt] of relations) { g[prev - 1].push(nxt - 1); indeg[nxt - 1]++; } const q: number[] = []; for (let i = 0; i < n; ++i) { if (indeg[i] === 0) { q.push(i); } } let ans = 0; while (q.length) { ++ans; for (let k = q.length; k; --k) { const i = q.shift()!; --n; for (const j of g[i]) { if (--indeg[j] === 0) { q.push(j); } } } } return n === 0 ? ans : -1; }