Welcome to Subscribe On Youtube
1038. Binary Search Tree to Greater Sum Tree
Description
Given the root of a Binary Search Tree (BST), convert it to a Greater Tree such that every key of the original BST is changed to the original key plus the sum of all keys greater than the original key in BST.
As a reminder, a binary search tree is a tree that satisfies these constraints:
- The left subtree of a node contains only nodes with keys less than the node's key.
- The right subtree of a node contains only nodes with keys greater than the node's key.
- Both the left and right subtrees must also be binary search trees.
Example 1:
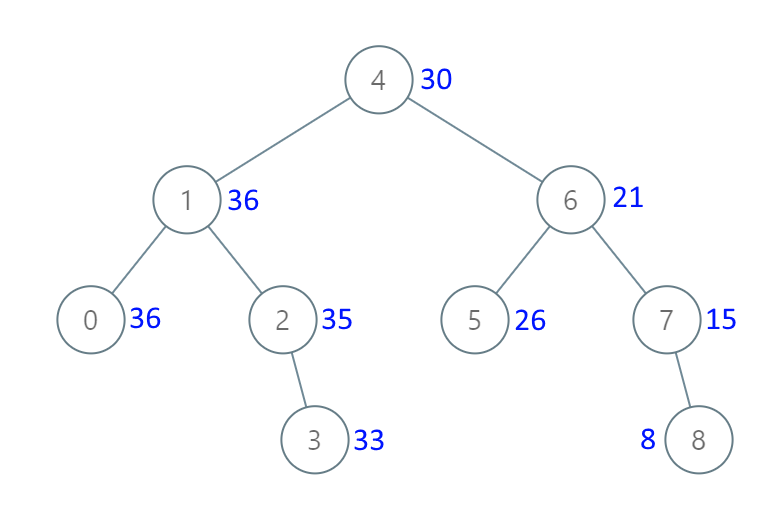
Input: root = [4,1,6,0,2,5,7,null,null,null,3,null,null,null,8] Output: [30,36,21,36,35,26,15,null,null,null,33,null,null,null,8]
Example 2:
Input: root = [0,null,1] Output: [1,null,1]
Constraints:
- The number of nodes in the tree is in the range
[1, 100]. 0 <= Node.val <= 100- All the values in the tree are unique.
Note: This question is the same as 538: https://leetcode.com/problems/convert-bst-to-greater-tree/
Solutions
-
/** * Definition for a binary tree node. * public class TreeNode { * int val; * TreeNode left; * TreeNode right; * TreeNode() {} * TreeNode(int val) { this.val = val; } * TreeNode(int val, TreeNode left, TreeNode right) { * this.val = val; * this.left = left; * this.right = right; * } * } */ class Solution { public TreeNode bstToGst(TreeNode root) { int s = 0; TreeNode node = root; while (root != null) { if (root.right == null) { s += root.val; root.val = s; root = root.left; } else { TreeNode next = root.right; while (next.left != null && next.left != root) { next = next.left; } if (next.left == null) { next.left = root; root = root.right; } else { s += root.val; root.val = s; next.left = null; root = root.left; } } } return node; } } -
/** * Definition for a binary tree node. * struct TreeNode { * int val; * TreeNode *left; * TreeNode *right; * TreeNode() : val(0), left(nullptr), right(nullptr) {} * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {} * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {} * }; */ class Solution { public: TreeNode* bstToGst(TreeNode* root) { int s = 0; TreeNode* node = root; while (root) { if (root->right == nullptr) { s += root->val; root->val = s; root = root->left; } else { TreeNode* next = root->right; while (next->left && next->left != root) { next = next->left; } if (next->left == nullptr) { next->left = root; root = root->right; } else { s += root->val; root->val = s; next->left = nullptr; root = root->left; } } } return node; } }; -
# Definition for a binary tree node. # class TreeNode: # def __init__(self, val=0, left=None, right=None): # self.val = val # self.left = left # self.right = right class Solution: def bstToGst(self, root: TreeNode) -> TreeNode: s = 0 node = root while root: if root.right is None: s += root.val root.val = s root = root.left else: next = root.right while next.left and next.left != root: next = next.left if next.left is None: next.left = root root = root.right else: s += root.val root.val = s next.left = None root = root.left return node -
/** * Definition for a binary tree node. * type TreeNode struct { * Val int * Left *TreeNode * Right *TreeNode * } */ func bstToGst(root *TreeNode) *TreeNode { s := 0 node := root for root != nil { if root.Right == nil { s += root.Val root.Val = s root = root.Left } else { next := root.Right for next.Left != nil && next.Left != root { next = next.Left } if next.Left == nil { next.Left = root root = root.Right } else { s += root.Val root.Val = s next.Left = nil root = root.Left } } } return node } -
/** * Definition for a binary tree node. * class TreeNode { * val: number * left: TreeNode | null * right: TreeNode | null * constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) { * this.val = (val===undefined ? 0 : val) * this.left = (left===undefined ? null : left) * this.right = (right===undefined ? null : right) * } * } */ function bstToGst(root: TreeNode | null): TreeNode | null { let cur = root; let sum = 0; while (cur != null) { const { val, left, right } = cur; if (right == null) { sum += val; cur.val = sum; cur = left; } else { let next = right; while (next.left != null && next.left != cur) { next = next.left; } if (next.left == null) { next.left = cur; cur = right; } else { next.left = null; sum += val; cur.val = sum; cur = left; } } } return root; } -
/** * Definition for a binary tree node. * function TreeNode(val, left, right) { * this.val = (val===undefined ? 0 : val) * this.left = (left===undefined ? null : left) * this.right = (right===undefined ? null : right) * } */ /** * @param {TreeNode} root * @return {TreeNode} */ var bstToGst = function (root) { let s = 0; function dfs(root) { if (!root) { return; } dfs(root.right); s += root.val; root.val = s; dfs(root.left); } dfs(root); return root; }; -
// Definition for a binary tree node. // #[derive(Debug, PartialEq, Eq)] // pub struct TreeNode { // pub val: i32, // pub left: Option<Rc<RefCell<TreeNode>>>, // pub right: Option<Rc<RefCell<TreeNode>>>, // } // // impl TreeNode { // #[inline] // pub fn new(val: i32) -> Self { // TreeNode { // val, // left: None, // right: None // } // } // } use std::rc::Rc; use std::cell::RefCell; impl Solution { fn dfs(root: &mut Option<Rc<RefCell<TreeNode>>>, mut sum: i32) -> i32 { if let Some(node) = root { let mut node = node.as_ref().borrow_mut(); sum = Self::dfs(&mut node.right, sum) + node.val; node.val = sum; sum = Self::dfs(&mut node.left, sum); } sum } pub fn bst_to_gst(mut root: Option<Rc<RefCell<TreeNode>>>) -> Option<Rc<RefCell<TreeNode>>> { Self::dfs(&mut root, 0); root } }