Welcome to Subscribe On Youtube
968. Binary Tree Cameras
Description
You are given the root of a binary tree. We install cameras on the tree nodes where each camera at a node can monitor its parent, itself, and its immediate children.
Return the minimum number of cameras needed to monitor all nodes of the tree.
Example 1:
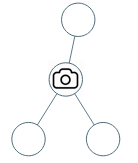
Input: root = [0,0,null,0,0] Output: 1 Explanation: One camera is enough to monitor all nodes if placed as shown.
Example 2:
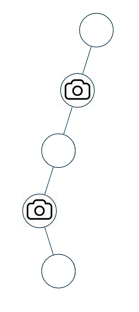
Input: root = [0,0,null,0,null,0,null,null,0] Output: 2 Explanation: At least two cameras are needed to monitor all nodes of the tree. The above image shows one of the valid configurations of camera placement.
Constraints:
- The number of nodes in the tree is in the range
[1, 1000]. Node.val == 0
Solutions
-
/** * Definition for a binary tree node. * public class TreeNode { * int val; * TreeNode left; * TreeNode right; * TreeNode() {} * TreeNode(int val) { this.val = val; } * TreeNode(int val, TreeNode left, TreeNode right) { * this.val = val; * this.left = left; * this.right = right; * } * } */ class Solution { public int minCameraCover(TreeNode root) { int[] ans = dfs(root); return Math.min(ans[0], ans[1]); } private int[] dfs(TreeNode root) { if (root == null) { return new int[] {1 << 29, 0, 0}; } var l = dfs(root.left); var r = dfs(root.right); int a = 1 + Math.min(Math.min(l[0], l[1]), l[2]) + Math.min(Math.min(r[0], r[1]), r[2]); int b = Math.min(Math.min(l[0] + r[1], l[1] + r[0]), l[0] + r[0]); int c = l[1] + r[1]; return new int[] {a, b, c}; } } -
/** * Definition for a binary tree node. * struct TreeNode { * int val; * TreeNode *left; * TreeNode *right; * TreeNode() : val(0), left(nullptr), right(nullptr) {} * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {} * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {} * }; */ struct Status { int a, b, c; }; class Solution { public: int minCameraCover(TreeNode* root) { auto [a, b, _] = dfs(root); return min(a, b); } Status dfs(TreeNode* root) { if (!root) { return {1 << 29, 0, 0}; } auto [la, lb, lc] = dfs(root->left); auto [ra, rb, rc] = dfs(root->right); int a = 1 + min({la, lb, lc}) + min({ra, rb, rc}); int b = min({la + ra, la + rb, lb + ra}); int c = lb + rb; return {a, b, c}; }; }; -
# Definition for a binary tree node. # class TreeNode: # def __init__(self, val=0, left=None, right=None): # self.val = val # self.left = left # self.right = right class Solution: def minCameraCover(self, root: Optional[TreeNode]) -> int: def dfs(root): if root is None: return inf, 0, 0 la, lb, lc = dfs(root.left) ra, rb, rc = dfs(root.right) a = min(la, lb, lc) + min(ra, rb, rc) + 1 b = min(la + rb, lb + ra, la + ra) c = lb + rb return a, b, c a, b, _ = dfs(root) return min(a, b) -
/** * Definition for a binary tree node. * type TreeNode struct { * Val int * Left *TreeNode * Right *TreeNode * } */ func minCameraCover(root *TreeNode) int { var dfs func(*TreeNode) (int, int, int) dfs = func(root *TreeNode) (int, int, int) { if root == nil { return 1 << 29, 0, 0 } la, lb, lc := dfs(root.Left) ra, rb, rc := dfs(root.Right) a := 1 + min(la, min(lb, lc)) + min(ra, min(rb, rc)) b := min(la+ra, min(la+rb, lb+ra)) c := lb + rb return a, b, c } a, b, _ := dfs(root) return min(a, b) } -
/** * Definition for a binary tree node. * class TreeNode { * val: number * left: TreeNode | null * right: TreeNode | null * constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) { * this.val = (val===undefined ? 0 : val) * this.left = (left===undefined ? null : left) * this.right = (right===undefined ? null : right) * } * } */ function minCameraCover(root: TreeNode | null): number { const dfs = (root: TreeNode | null): number[] => { if (!root) { return [1 << 29, 0, 0]; } const [la, lb, lc] = dfs(root.left); const [ra, rb, rc] = dfs(root.right); const a = 1 + Math.min(la, lb, lc) + Math.min(ra, rb, rc); const b = Math.min(la + ra, la + rb, lb + ra); const c = lb + rb; return [a, b, c]; }; const [a, b, _] = dfs(root); return Math.min(a, b); }