Welcome to Subscribe On Youtube
750. Number Of Corner Rectangles
Description
Given an m x n integer matrix grid where each entry is only 0 or 1, return the number of corner rectangles.
A corner rectangle is four distinct 1's on the grid that forms an axis-aligned rectangle. Note that only the corners need to have the value 1. Also, all four 1's used must be distinct.
Example 1:
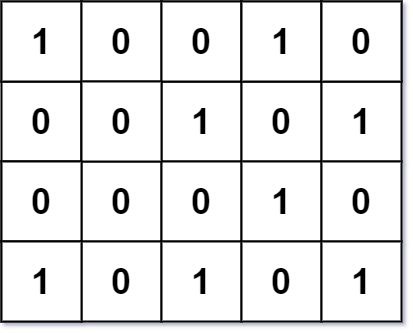
Input: grid = [[1,0,0,1,0],[0,0,1,0,1],[0,0,0,1,0],[1,0,1,0,1]] Output: 1 Explanation: There is only one corner rectangle, with corners grid[1][2], grid[1][4], grid[3][2], grid[3][4].
Example 2:

Input: grid = [[1,1,1],[1,1,1],[1,1,1]] Output: 9 Explanation: There are four 2x2 rectangles, four 2x3 and 3x2 rectangles, and one 3x3 rectangle.
Example 3:
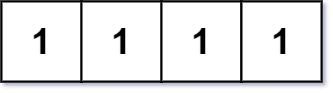
Input: grid = [[1,1,1,1]] Output: 0 Explanation: Rectangles must have four distinct corners.
Constraints:
m == grid.lengthn == grid[i].length1 <= m, n <= 200grid[i][j]is either0or1.- The number of
1's in the grid is in the range[1, 6000].
Solutions
Solution 1: Hash Table + Enumeration
We enumerate each row as the bottom of the rectangle. For the current row, if both column $i$ and column $j$ are $1$, then we use a hash table to find out how many of the previous rows have both columns $i$ and $j$ as $1$. This is the number of rectangles with $(i, j)$ as the bottom right corner, and we add this number to the answer. Then we add $(i, j)$ to the hash table and continue to enumerate the next pair $(i, j)$.
The time complexity is $O(m \times n^2)$, and the space complexity is $O(n^2)$. Here, $m$ and $n$ are the number of rows and columns of the matrix, respectively.
-
class Solution { public int countCornerRectangles(int[][] grid) { int n = grid[0].length; int ans = 0; Map<List<Integer>, Integer> cnt = new HashMap<>(); for (var row : grid) { for (int i = 0; i < n; ++i) { if (row[i] == 1) { for (int j = i + 1; j < n; ++j) { if (row[j] == 1) { List<Integer> t = List.of(i, j); ans += cnt.getOrDefault(t, 0); cnt.merge(t, 1, Integer::sum); } } } } } return ans; } } -
class Solution { public: int countCornerRectangles(vector<vector<int>>& grid) { int n = grid[0].size(); int ans = 0; map<pair<int, int>, int> cnt; for (auto& row : grid) { for (int i = 0; i < n; ++i) { if (row[i]) { for (int j = i + 1; j < n; ++j) { if (row[j]) { ans += cnt[{i, j}]; ++cnt[{i, j}]; } } } } } return ans; } }; -
class Solution: def countCornerRectangles(self, grid: List[List[int]]) -> int: ans = 0 cnt = Counter() n = len(grid[0]) for row in grid: for i, c1 in enumerate(row): if c1: for j in range(i + 1, n): if row[j]: ans += cnt[(i, j)] cnt[(i, j)] += 1 return ans -
func countCornerRectangles(grid [][]int) (ans int) { n := len(grid[0]) type pair struct{ x, y int } cnt := map[pair]int{} for _, row := range grid { for i, x := range row { if x == 1 { for j := i + 1; j < n; j++ { if row[j] == 1 { t := pair{i, j} ans += cnt[t] cnt[t]++ } } } } } return } -
function countCornerRectangles(grid: number[][]): number { const n = grid[0].length; let ans = 0; const cnt: Map<number, number> = new Map(); for (const row of grid) { for (let i = 0; i < n; ++i) { if (row[i] === 1) { for (let j = i + 1; j < n; ++j) { if (row[j] === 1) { const t = i * 200 + j; ans += cnt.get(t) ?? 0; cnt.set(t, (cnt.get(t) ?? 0) + 1); } } } } } return ans; }