749. Contain Virus

Description

A virus is spreading rapidly, and your task is to quarantine the infected area by installing walls.

The world is modeled as an m x n binary grid isInfected, where isInfected[i][j] == 0 represents uninfected cells, and isInfected[i][j] == 1 represents cells contaminated with the virus. A wall (and only one wall) can be installed between any two 4-directionally adjacent cells, on the shared boundary.

Every night, the virus spreads to all neighboring cells in all four directions unless blocked by a wall. Resources are limited. Each day, you can install walls around only one region (i.e., the affected area (continuous block of infected cells) that threatens the most uninfected cells the following night). There will never be a tie.

Return the number of walls used to quarantine all the infected regions. If the world will become fully infected, return the number of walls used.

Example 1:

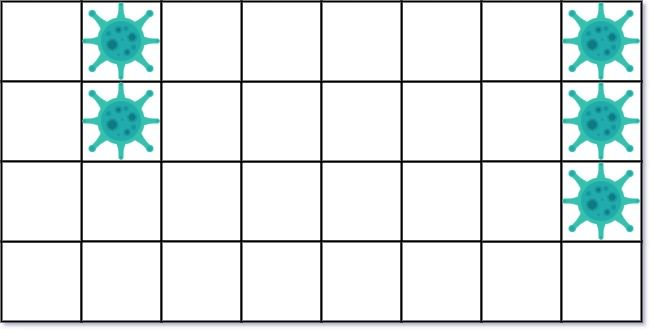
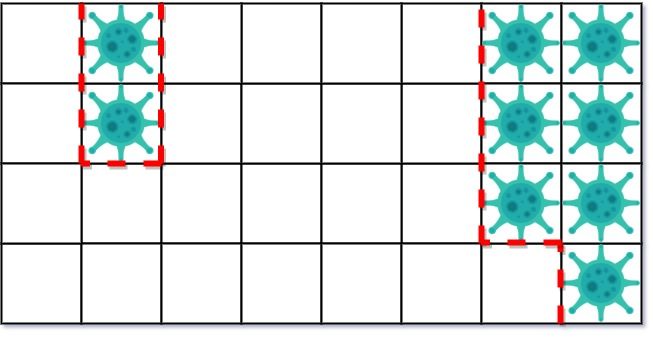
Input: isInfected = [[0,1,0,0,0,0,0,1],[0,1,0,0,0,0,0,1],[0,0,0,0,0,0,0,1],[0,0,0,0,0,0,0,0]]
Output: 10
Explanation: There are 2 contaminated regions.
On the first day, add 5 walls to quarantine the viral region on the left. The board after the virus spreads is:

On the second day, add 5 walls to quarantine the viral region on the right. The virus is fully contained.

Example 2:

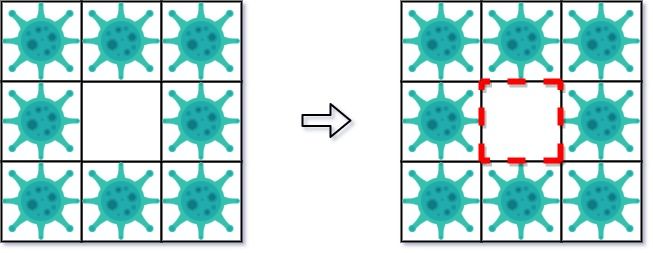
Input: isInfected = [[1,1,1],[1,0,1],[1,1,1]]
Output: 4
Explanation: Even though there is only one cell saved, there are 4 walls built.
Notice that walls are only built on the shared boundary of two different cells.

Example 3:

Input: isInfected = [[1,1,1,0,0,0,0,0,0],[1,0,1,0,1,1,1,1,1],[1,1,1,0,0,0,0,0,0]]
Output: 13
Explanation: The region on the left only builds two new walls.

Constraints:

m == isInfected.length
n == isInfected[i].length
1 <= m, n <= 50
isInfected[i][j] is either 0 or 1.
There is always a contiguous viral region throughout the described process that will infect strictly more uncontaminated squares in the next round.

Solutions

class Solution {
    private static final int[] DIRS = {-1, 0, 1, 0, -1};
    private List<Integer> c = new ArrayList<>();
    private List<List<Integer>> areas = new ArrayList<>();
    private List<Set<Integer>> boundaries = new ArrayList<>();
    private int[][] infected;
    private boolean[][] vis;
    private int m;
    private int n;

    public int containVirus(int[][] isInfected) {
        infected = isInfected;
        m = infected.length;
        n = infected[0].length;
        vis = new boolean[m][n];
        int ans = 0;
        while (true) {
            for (boolean[] row : vis) {
                Arrays.fill(row, false);
            }
            c.clear();
            areas.clear();
            boundaries.clear();
            for (int i = 0; i < m; ++i) {
                for (int j = 0; j < n; ++j) {
                    if (infected[i][j] == 1 && !vis[i][j]) {
                        c.add(0);
                        areas.add(new ArrayList<>());
                        boundaries.add(new HashSet<>());
                        dfs(i, j);
                    }
                }
            }
            if (areas.isEmpty()) {
                break;
            }
            int idx = max(boundaries);
            ans += c.get(idx);
            for (int t = 0; t < areas.size(); ++t) {
                if (t == idx) {
                    for (int v : areas.get(t)) {
                        int i = v / n, j = v % n;
                        infected[i][j] = -1;
                    }
                } else {
                    for (int v : areas.get(t)) {
                        int i = v / n, j = v % n;
                        for (int k = 0; k < 4; ++k) {
                            int x = i + DIRS[k], y = j + DIRS[k + 1];
                            if (x >= 0 && x < m && y >= 0 && y < n && infected[x][y] == 0) {
                                infected[x][y] = 1;
                            }
                        }
                    }
                }
            }
        }
        return ans;
    }

    private int max(List<Set<Integer>> boundaries) {
        int idx = 0;
        int mx = boundaries.get(0).size();
        for (int i = 1; i < boundaries.size(); ++i) {
            int t = boundaries.get(i).size();
            if (mx < t) {
                mx = t;
                idx = i;
            }
        }
        return idx;
    }

    private void dfs(int i, int j) {
        vis[i][j] = true;
        int idx = areas.size() - 1;
        areas.get(idx).add(i * n + j);
        for (int k = 0; k < 4; ++k) {
            int x = i + DIRS[k], y = j + DIRS[k + 1];
            if (x >= 0 && x < m && y >= 0 && y < n) {
                if (infected[x][y] == 1 && !vis[x][y]) {
                    dfs(x, y);
                } else if (infected[x][y] == 0) {
                    c.set(idx, c.get(idx) + 1);
                    boundaries.get(idx).add(x * n + y);
                }
            }
        }
    }
}

class Solution {
public:
    const vector<int> dirs = {-1, 0, 1, 0, -1};
    vector<int> c;
    vector<vector<int>> areas;
    vector<unordered_set<int>> boundaries;
    vector<vector<int>> infected;
    vector<vector<bool>> vis;
    int m;
    int n;

    int containVirus(vector<vector<int>>& isInfected) {
        infected = isInfected;
        m = infected.size();
        n = infected[0].size();
        vis.assign(m, vector<bool>(n));
        int ans = 0;
        while (1) {
            for (int i = 0; i < m; ++i)
                for (int j = 0; j < n; ++j) vis[i][j] = false;
            c.clear();
            areas.clear();
            boundaries.clear();
            for (int i = 0; i < m; ++i) {
                for (int j = 0; j < n; ++j) {
                    if (infected[i][j] == 1 && !vis[i][j]) {
                        c.push_back(0);
                        areas.push_back({});
                        boundaries.push_back({});
                        dfs(i, j);
                    }
                }
            }
            if (areas.empty()) break;
            int idx = getMax();
            ans += c[idx];
            for (int t = 0; t < areas.size(); ++t) {
                if (t == idx) {
                    for (int v : areas[t]) {
                        int i = v / n, j = v % n;
                        infected[i][j] = -1;
                    }
                } else {
                    for (int v : areas[t]) {
                        int i = v / n, j = v % n;
                        for (int k = 0; k < 4; ++k) {
                            int x = i + dirs[k], y = j + dirs[k + 1];
                            if (x >= 0 && x < m && y >= 0 && y < n && infected[x][y] == 0) infected[x][y] = 1;
                        }
                    }
                }
            }
        }
        return ans;
    }

    int getMax() {
        int idx = 0;
        int mx = boundaries[0].size();
        for (int i = 1; i < boundaries.size(); ++i) {
            int t = boundaries[i].size();
            if (mx < t) {
                mx = t;
                idx = i;
            }
        }
        return idx;
    }

    void dfs(int i, int j) {
        vis[i][j] = true;
        areas.back().push_back(i * n + j);
        for (int k = 0; k < 4; ++k) {
            int x = i + dirs[k], y = j + dirs[k + 1];
            if (x >= 0 && x < m && y >= 0 && y < n) {
                if (infected[x][y] == 1 && !vis[x][y])
                    dfs(x, y);
                else if (infected[x][y] == 0) {
                    c.back() += 1;
                    boundaries.back().insert(x * n + y);
                }
            }
        }
    }
};

class Solution:
    def containVirus(self, isInfected: List[List[int]]) -> int:
        def dfs(i, j):
            vis[i][j] = True
            areas[-1].append((i, j))
            for a, b in [[0, -1], [0, 1], [-1, 0], [1, 0]]:
                x, y = i + a, j + b
                if 0 <= x < m and 0 <= y < n:
                    if isInfected[x][y] == 1 and not vis[x][y]:
                        dfs(x, y)
                    elif isInfected[x][y] == 0:
                        c[-1] += 1
                        boundaries[-1].add((x, y))

        m, n = len(isInfected), len(isInfected[0])
        ans = 0
        while 1:
            vis = [[False] * n for _ in range(m)]
            areas = []
            c = []
            boundaries = []
            for i, row in enumerate(isInfected):
                for j, v in enumerate(row):
                    if v == 1 and not vis[i][j]:
                        areas.append([])
                        boundaries.append(set())
                        c.append(0)
                        dfs(i, j)
            if not areas:
                break
            idx = boundaries.index(max(boundaries, key=len))
            ans += c[idx]
            for k, area in enumerate(areas):
                if k == idx:
                    for i, j in area:
                        isInfected[i][j] = -1
                else:
                    for i, j in area:
                        for a, b in [[0, -1], [0, 1], [-1, 0], [1, 0]]:
                            x, y = i + a, j + b
                            if 0 <= x < m and 0 <= y < n and isInfected[x][y] == 0:
                                isInfected[x][y] = 1
        return ans

func containVirus(isInfected [][]int) int {
	m, n := len(isInfected), len(isInfected[0])
	ans := 0
	dirs := []int{-1, 0, 1, 0, -1}
	max := func(boundaries []map[int]bool) int {
		idx := 0
		mx := len(boundaries[0])
		for i, v := range boundaries {
			t := len(v)
			if mx < t {
				mx = t
				idx = i
			}
		}
		return idx
	}

	for {
		vis := make([][]bool, m)
		for i := range vis {
			vis[i] = make([]bool, n)
		}
		areas := []map[int]bool{}
		boundaries := []map[int]bool{}
		c := []int{}

		var dfs func(i, j int)
		dfs = func(i, j int) {
			vis[i][j] = true
			idx := len(areas) - 1
			areas[idx][i*n+j] = true
			for k := 0; k < 4; k++ {
				x, y := i+dirs[k], j+dirs[k+1]
				if x >= 0 && x < m && y >= 0 && y < n {
					if isInfected[x][y] == 1 && !vis[x][y] {
						dfs(x, y)
					} else if isInfected[x][y] == 0 {
						c[idx]++
						boundaries[idx][x*n+y] = true
					}
				}
			}
		}

		for i, row := range isInfected {
			for j, v := range row {
				if v == 1 && !vis[i][j] {
					areas = append(areas, map[int]bool{})
					boundaries = append(boundaries, map[int]bool{})
					c = append(c, 0)
					dfs(i, j)
				}
			}
		}
		if len(areas) == 0 {
			break
		}
		idx := max(boundaries)
		ans += c[idx]
		for t, area := range areas {
			if t == idx {
				for v := range area {
					i, j := v/n, v%n
					isInfected[i][j] = -1
				}
			} else {
				for v := range area {
					i, j := v/n, v%n
					for k := 0; k < 4; k++ {
						x, y := i+dirs[k], j+dirs[k+1]
						if x >= 0 && x < m && y >= 0 && y < n && isInfected[x][y] == 0 {
							isInfected[x][y] = 1
						}
					}
				}
			}
		}

	}
	return ans
}

749 - Contain Virus

749. Contain Virus

Description

Solutions

All Problems

All Solutions

Welcome to Subscribe On Youtube

749. Contain Virus

Description

Solutions

All Problems

All Solutions