Welcome to Subscribe On Youtube
364. Nested List Weight Sum II
Description
You are given a nested list of integers nestedList. Each element is either an integer or a list whose elements may also be integers or other lists.
The depth of an integer is the number of lists that it is inside of. For example, the nested list [1,[2,2],[[3],2],1] has each integer's value set to its depth. Let maxDepth be the maximum depth of any integer.
The weight of an integer is maxDepth - (the depth of the integer) + 1.
Return the sum of each integer in nestedList multiplied by its weight.
Example 1:
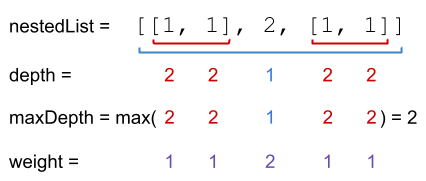
Input: nestedList = [[1,1],2,[1,1]] Output: 8 Explanation: Four 1's with a weight of 1, one 2 with a weight of 2. 1*1 + 1*1 + 2*2 + 1*1 + 1*1 = 8
Example 2:
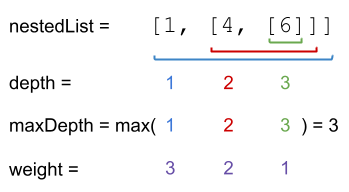
Input: nestedList = [1,[4,[6]]] Output: 17 Explanation: One 1 at depth 3, one 4 at depth 2, and one 6 at depth 1. 1*3 + 4*2 + 6*1 = 17
Constraints:
1 <= nestedList.length <= 50- The values of the integers in the nested list is in the range
[-100, 100]. - The maximum depth of any integer is less than or equal to
50.
Solutions - 1, two passes
Straightforward solution is 2 passes
- 1st pass to depth first
- then calculate
Solutions - 2, one pass
And moreover, below is another way of solving it via only 1-pass.
Explanation of the 1-pass Approach
The solution uses an iterative approach to traverse the nested list level by level, starting from the outermost level (level 1) and moving inward. It keeps track of two sums:
unweighted: The cumulative sum of all integers encountered so far, regardless of their depth.weighted: The weighted sum, which is recalculated at each level to reflect the increasing weight of previously encountered integers as the traversal goes deeper.
-
Initialization: If the input list is empty, the function immediately returns
0. This check is technically redundant due to Python’s treatment of empty lists as falsy values, which would naturally terminate the loop. -
Iterative Traversal: The solution iteratively traverses the nested list. At each iteration, it processes one level of the list.
-
Accumulating
unweightedSum: For each elementain the current level (nestedList), ifais an integer, its value is added tounweighted. This sum accumulates values from all levels processed so far but does not account for their depth. -
Preparing for Next Level: If
ais not an integer but another nested list, the elements of this list are added tonext_level, preparing them for processing in the next iteration.
-
-
Updating
weightedSum: After processing each level,weightedis increased byunweighted. This step is crucial because it effectively adds theunweightedsum repeatedly, once for each level of depth, thereby inversely weighting the depth. Deeper integers have already contributed tounweightedin earlier iterations, so they are counted multiple times inweighted, reflecting their deeper level. -
Moving to the Next Level: The list to be processed in the next iteration is updated to
next_level, moving the traversal one level deeper into the nested list structure. -
Returning the Result: Once all levels have been processed and there are no more elements to traverse, the
weightedsum represents the inverse depth sum of the original nested list, and it is returned as the result.
Example
Consider the nested list [[1,1],2,[1,1]]. The inverse depth sum is calculated as follows:
- At the outermost level, the sum of integers is
2(only the integer2is at this level). This value is added toweighted. Soweighted=2andunweighted=2 - At the next level, the sum of integers is
4(from the four1s in the nested lists). This sum is added tounweightedmaking it6(once for this level and once from the previous level’sunweightedsum2).
The final weighted sum is weighted + unweighted, i.e. 2 + 6 = 8, which is the inverse depth sum of the nested list.
This approach efficiently calculates the inverse depth sum without needing to explicitly track the depth of each integer, leveraging the iterative re-accumulation of unweighted sums to achieve the correct weighting.
-
/** * // This is the interface that allows for creating nested lists. * // You should not implement it, or speculate about its implementation * public interface NestedInteger { * // Constructor initializes an empty nested list. * public NestedInteger(); * * // Constructor initializes a single integer. * public NestedInteger(int value); * * // @return true if this NestedInteger holds a single integer, rather than a nested list. * public boolean isInteger(); * * // @return the single integer that this NestedInteger holds, if it holds a single integer * // Return null if this NestedInteger holds a nested list * public Integer getInteger(); * * // Set this NestedInteger to hold a single integer. * public void setInteger(int value); * * // Set this NestedInteger to hold a nested list and adds a nested integer to it. * public void add(NestedInteger ni); * * // @return the nested list that this NestedInteger holds, if it holds a nested list * // Return empty list if this NestedInteger holds a single integer * public List<NestedInteger> getList(); * } */ class Solution { public int depthSumInverse(List<NestedInteger> nestedList) { int depth = maxDepth(nestedList); return dfs(nestedList, depth); } private int maxDepth(List<NestedInteger> nestedList) { int depth = 1; for (NestedInteger item : nestedList) { if (item.isInteger()) { continue; } depth = Math.max(depth, 1 + maxDepth(item.getList())); } return depth; } private int dfs(List<NestedInteger> nestedList, int depth) { int depthSum = 0; for (NestedInteger item : nestedList) { if (item.isInteger()) { depthSum += item.getInteger() * depth; } else { depthSum += dfs(item.getList(), depth - 1); } } return depthSum; } } -
# """ # This is the interface that allows for creating nested lists. # You should not implement it, or speculate about its implementation # """ # class NestedInteger: # def __init__(self, value=None): # """ # If value is not specified, initializes an empty list. # Otherwise initializes a single integer equal to value. # """ # # def isInteger(self): # """ # @return True if this NestedInteger holds a single integer, rather than a nested list. # :rtype bool # """ # # def add(self, elem): # """ # Set this NestedInteger to hold a nested list and adds a nested integer elem to it. # :rtype void # """ # # def setInteger(self, value): # """ # Set this NestedInteger to hold a single integer equal to value. # :rtype void # """ # # def getInteger(self): # """ # @return the single integer that this NestedInteger holds, if it holds a single integer # Return None if this NestedInteger holds a nested list # :rtype int # """ # # def getList(self): # """ # @return the nested list that this NestedInteger holds, if it holds a nested list # Return None if this NestedInteger holds a single integer # :rtype List[NestedInteger] # """ class Solution: def depthSumInverse(self, nestedList: List[NestedInteger]) -> int: def max_depth(nestedList): depth = 1 for item in nestedList: if item.isInteger(): continue depth = max(depth, max_depth(item.getList()) + 1) return depth def dfs(nestedList, max_depth): depth_sum = 0 for item in nestedList: if item.isInteger(): depth_sum += item.getInteger() * max_depth else: depth_sum += dfs(item.getList(), max_depth - 1) return depth_sum depth = max_depth(nestedList) return dfs(nestedList, depth) ############ class Solution_onePass: # iterative def depthSumInverse(self, nestedList: List[NestedInteger]) -> int: if not nestedList: # can remove this check, an empty list in Python is considered "falsy" # and the loop will exit when it reaches the end of the list return 0 # weighted is like previous round result unweighted = weighted = 0 while nestedList: next_level = [] for a in nestedList: if a.isInteger(): unweighted += a.getInteger() else: next_level.extend(a.getList()) weighted += unweighted nestedList = next_level return weighted -
/** * // This is the interface that allows for creating nested lists. * // You should not implement it, or speculate about its implementation * function NestedInteger() { * * Return true if this NestedInteger holds a single integer, rather than a nested list. * @return {boolean} * this.isInteger = function() { * ... * }; * * Return the single integer that this NestedInteger holds, if it holds a single integer * Return null if this NestedInteger holds a nested list * @return {integer} * this.getInteger = function() { * ... * }; * * Set this NestedInteger to hold a single integer equal to value. * @return {void} * this.setInteger = function(value) { * ... * }; * * Set this NestedInteger to hold a nested list and adds a nested integer elem to it. * @return {void} * this.add = function(elem) { * ... * }; * * Return the nested list that this NestedInteger holds, if it holds a nested list * Return null if this NestedInteger holds a single integer * @return {NestedInteger[]} * this.getList = function() { * ... * }; * }; */ /** * @param {NestedInteger[]} nestedList * @return {number} */ var depthSumInverse = function (nestedList) { const maxDepth = nestedList => { let depth = 1; for (const item of nestedList) { if (item.isInteger()) { continue; } depth = Math.max(depth, 1 + maxDepth(item.getList())); } return depth; }; const dfs = (nestedList, depth) => { let depthSum = 0; for (const item of nestedList) { if (item.isInteger()) { depthSum += item.getInteger() * depth; } else { depthSum += dfs(item.getList(), depth - 1); } } return depthSum; }; const depth = maxDepth(nestedList); return dfs(nestedList, depth); }; -
/** * // This is the interface that allows for creating nested lists. * // You should not implement it, or speculate about its implementation * class NestedInteger { * public: * // Constructor initializes an empty nested list. * NestedInteger(); * * // Constructor initializes a single integer. * NestedInteger(int value); * * // Return true if this NestedInteger holds a single integer, rather than a nested list. * bool isInteger() const; * * // Return the single integer that this NestedInteger holds, if it holds a single integer * // The result is undefined if this NestedInteger holds a nested list * int getInteger() const; * * // Set this NestedInteger to hold a single integer. * void setInteger(int value); * * // Set this NestedInteger to hold a nested list and adds a nested integer to it. * void add(const NestedInteger &ni); * * // Return the nested list that this NestedInteger holds, if it holds a nested list * // The result is undefined if this NestedInteger holds a single integer * const vector<NestedInteger> &getList() const; * }; */ class Solution { public: int depthSumInverse(vector<NestedInteger>& nestedList) { int maxDepth = 0, ws = 0, s = 0; function<void(NestedInteger&, int)> dfs = [&](NestedInteger& x, int d) { maxDepth = max(maxDepth, d); if (x.isInteger()) { ws += x.getInteger() * d; s += x.getInteger(); } else { for (auto& y : x.getList()) { dfs(y, d + 1); } } }; for (auto& x : nestedList) { dfs(x, 1); } return (maxDepth + 1) * s - ws; } }; -
/** * // This is the interface that allows for creating nested lists. * // You should not implement it, or speculate about its implementation * type NestedInteger struct { * } * * // Return true if this NestedInteger holds a single integer, rather than a nested list. * func (n NestedInteger) IsInteger() bool {} * * // Return the single integer that this NestedInteger holds, if it holds a single integer * // The result is undefined if this NestedInteger holds a nested list * // So before calling this method, you should have a check * func (n NestedInteger) GetInteger() int {} * * // Set this NestedInteger to hold a single integer. * func (n *NestedInteger) SetInteger(value int) {} * * // Set this NestedInteger to hold a nested list and adds a nested integer to it. * func (n *NestedInteger) Add(elem NestedInteger) {} * * // Return the nested list that this NestedInteger holds, if it holds a nested list * // The list length is zero if this NestedInteger holds a single integer * // You can access NestedInteger's List element directly if you want to modify it * func (n NestedInteger) GetList() []*NestedInteger {} */ func depthSumInverse(nestedList []*NestedInteger) int { var maxDepth, ws, s int var dfs func(*NestedInteger, int) dfs = func(x *NestedInteger, d int) { maxDepth = max(maxDepth, d) if x.IsInteger() { ws += x.GetInteger() * d s += x.GetInteger() } else { for _, y := range x.GetList() { dfs(y, d+1) } } } for _, x := range nestedList { dfs(x, 1) } return (maxDepth+1)*s - ws } -
/** * // This is the interface that allows for creating nested lists. * // You should not implement it, or speculate about its implementation * class NestedInteger { * If value is provided, then it holds a single integer * Otherwise it holds an empty nested list * constructor(value?: number) { * ... * }; * * Return true if this NestedInteger holds a single integer, rather than a nested list. * isInteger(): boolean { * ... * }; * * Return the single integer that this NestedInteger holds, if it holds a single integer * Return null if this NestedInteger holds a nested list * getInteger(): number | null { * ... * }; * * Set this NestedInteger to hold a single integer equal to value. * setInteger(value: number) { * ... * }; * * Set this NestedInteger to hold a nested list and adds a nested integer elem to it. * add(elem: NestedInteger) { * ... * }; * * Return the nested list that this NestedInteger holds, * or an empty list if this NestedInteger holds a single integer * getList(): NestedInteger[] { * ... * }; * }; */ function depthSumInverse(nestedList: NestedInteger[]): number { let [maxDepth, ws, s] = [0, 0, 0]; const dfs = (x: NestedInteger, d: number) => { maxDepth = Math.max(maxDepth, d); if (x.isInteger()) { ws += x.getInteger() * d; s += x.getInteger(); } else { for (const y of x.getList()) { dfs(y, d + 1); } } }; for (const x of nestedList) { dfs(x, 1); } return (maxDepth + 1) * s - ws; }