Welcome to Subscribe On Youtube
363. Max Sum of Rectangle No Larger Than K
Description
Given an m x n matrix matrix and an integer k, return the max sum of a rectangle in the matrix such that its sum is no larger than k.
It is guaranteed that there will be a rectangle with a sum no larger than k.
Example 1:
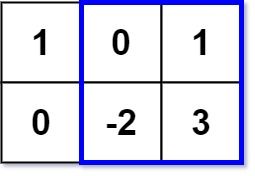
Input: matrix = [[1,0,1],[0,-2,3]], k = 2 Output: 2 Explanation: Because the sum of the blue rectangle [[0, 1], [-2, 3]] is 2, and 2 is the max number no larger than k (k = 2).
Example 2:
Input: matrix = [[2,2,-1]], k = 3 Output: 3
Constraints:
m == matrix.lengthn == matrix[i].length1 <= m, n <= 100-100 <= matrix[i][j] <= 100-105 <= k <= 105
Follow up: What if the number of rows is much larger than the number of columns?
Solutions
-
class Solution { public int maxSumSubmatrix(int[][] matrix, int k) { int m = matrix.length; int n = matrix[0].length; final int inf = 1 << 30; int ans = -inf; for (int i = 0; i < m; ++i) { int[] nums = new int[n]; for (int j = i; j < m; ++j) { for (int h = 0; h < n; ++h) { nums[h] += matrix[j][h]; } int s = 0; TreeSet<Integer> ts = new TreeSet<>(); ts.add(0); for (int x : nums) { s += x; Integer y = ts.ceiling(s - k); if (y != null) { ans = Math.max(ans, s - y); } ts.add(s); } } } return ans; } } -
class Solution { public: int maxSumSubmatrix(vector<vector<int>>& matrix, int k) { int m = matrix.size(), n = matrix[0].size(); const int inf = 1 << 30; int ans = -inf; for (int i = 0; i < m; ++i) { vector<int> nums(n); for (int j = i; j < m; ++j) { for (int h = 0; h < n; ++h) { nums[h] += matrix[j][h]; } set<int> ts; int s = 0; ts.insert(0); for (int x : nums) { s += x; auto it = ts.lower_bound(s - k); if (it != ts.end()) { ans = max(ans, s - *it); } ts.insert(s); } } } return ans; } }; -
from sortedcontainers import SortedSet class Solution: def maxSumSubmatrix(self, matrix: List[List[int]], k: int) -> int: m, n = len(matrix), len(matrix[0]) ans = -inf for i in range(m): nums = [0] * n for j in range(i, m): for h in range(n): nums[h] += matrix[j][h] s = 0 ts = SortedSet([0]) for x in nums: s += x p = ts.bisect_left(s - k) if p != len(ts): ans = max(ans, s - ts[p]) ts.add(s) return ans -
func maxSumSubmatrix(matrix [][]int, k int) int { m, n := len(matrix), len(matrix[0]) const inf = 1 << 30 ans := -inf for i := 0; i < m; i++ { nums := make([]int, n) for j := i; j < m; j++ { for h := 0; h < n; h++ { nums[h] += matrix[j][h] } s := 0 rbt := redblacktree.NewWithIntComparator() rbt.Put(0, nil) for _, x := range nums { s += x if y, ok := rbt.Ceiling(s - k); ok { ans = max(ans, s-y.Key.(int)) } rbt.Put(s, nil) } } } return ans } -
function maxSumSubmatrix(matrix: number[][], k: number): number { const m = matrix.length; const n = matrix[0].length; let ans = -Infinity; for (let i = 0; i < m; ++i) { const nums: number[] = new Array(n).fill(0); for (let j = i; j < m; ++j) { for (let h = 0; h < n; ++h) { nums[h] += matrix[j][h]; } let s = 0; const ts: TreeSet<number> = new TreeSet<number>(); ts.add(0); for (const x of nums) { s += x; const p = ts.ceil(s - k); if (p !== undefined) { ans = Math.max(ans, s - p); } ts.add(s); } } } return ans; } type Compare<T> = (lhs: T, rhs: T) => number; class RBTreeNode<T = number> { data: T; count: number; left: RBTreeNode<T> | null; right: RBTreeNode<T> | null; parent: RBTreeNode<T> | null; color: number; constructor(data: T) { this.data = data; this.left = this.right = this.parent = null; this.color = 0; this.count = 1; } sibling(): RBTreeNode<T> | null { if (!this.parent) return null; // sibling null if no parent return this.isOnLeft() ? this.parent.right : this.parent.left; } isOnLeft(): boolean { return this === this.parent!.left; } hasRedChild(): boolean { return ( Boolean(this.left && this.left.color === 0) || Boolean(this.right && this.right.color === 0) ); } } class RBTree<T> { root: RBTreeNode<T> | null; lt: (l: T, r: T) => boolean; constructor(compare: Compare<T> = (l: T, r: T) => (l < r ? -1 : l > r ? 1 : 0)) { this.root = null; this.lt = (l: T, r: T) => compare(l, r) < 0; } rotateLeft(pt: RBTreeNode<T>): void { const right = pt.right!; pt.right = right.left; if (pt.right) pt.right.parent = pt; right.parent = pt.parent; if (!pt.parent) this.root = right; else if (pt === pt.parent.left) pt.parent.left = right; else pt.parent.right = right; right.left = pt; pt.parent = right; } rotateRight(pt: RBTreeNode<T>): void { const left = pt.left!; pt.left = left.right; if (pt.left) pt.left.parent = pt; left.parent = pt.parent; if (!pt.parent) this.root = left; else if (pt === pt.parent.left) pt.parent.left = left; else pt.parent.right = left; left.right = pt; pt.parent = left; } swapColor(p1: RBTreeNode<T>, p2: RBTreeNode<T>): void { const tmp = p1.color; p1.color = p2.color; p2.color = tmp; } swapData(p1: RBTreeNode<T>, p2: RBTreeNode<T>): void { const tmp = p1.data; p1.data = p2.data; p2.data = tmp; } fixAfterInsert(pt: RBTreeNode<T>): void { let parent = null; let grandParent = null; while (pt !== this.root && pt.color !== 1 && pt.parent?.color === 0) { parent = pt.parent; grandParent = pt.parent.parent; /* Case : A Parent of pt is left child of Grand-parent of pt */ if (parent === grandParent?.left) { const uncle = grandParent.right; /* Case : 1 The uncle of pt is also red Only Recoloring required */ if (uncle && uncle.color === 0) { grandParent.color = 0; parent.color = 1; uncle.color = 1; pt = grandParent; } else { /* Case : 2 pt is right child of its parent Left-rotation required */ if (pt === parent.right) { this.rotateLeft(parent); pt = parent; parent = pt.parent; } /* Case : 3 pt is left child of its parent Right-rotation required */ this.rotateRight(grandParent); this.swapColor(parent!, grandParent); pt = parent!; } } else { /* Case : B Parent of pt is right child of Grand-parent of pt */ const uncle = grandParent!.left; /* Case : 1 The uncle of pt is also red Only Recoloring required */ if (uncle != null && uncle.color === 0) { grandParent!.color = 0; parent.color = 1; uncle.color = 1; pt = grandParent!; } else { /* Case : 2 pt is left child of its parent Right-rotation required */ if (pt === parent.left) { this.rotateRight(parent); pt = parent; parent = pt.parent; } /* Case : 3 pt is right child of its parent Left-rotation required */ this.rotateLeft(grandParent!); this.swapColor(parent!, grandParent!); pt = parent!; } } } this.root!.color = 1; } delete(val: T): boolean { const node = this.find(val); if (!node) return false; node.count--; if (!node.count) this.deleteNode(node); return true; } deleteAll(val: T): boolean { const node = this.find(val); if (!node) return false; this.deleteNode(node); return true; } deleteNode(v: RBTreeNode<T>): void { const u = BSTreplace(v); // True when u and v are both black const uvBlack = (u === null || u.color === 1) && v.color === 1; const parent = v.parent!; if (!u) { // u is null therefore v is leaf if (v === this.root) this.root = null; // v is root, making root null else { if (uvBlack) { // u and v both black // v is leaf, fix double black at v this.fixDoubleBlack(v); } else { // u or v is red if (v.sibling()) { // sibling is not null, make it red" v.sibling()!.color = 0; } } // delete v from the tree if (v.isOnLeft()) parent.left = null; else parent.right = null; } return; } if (!v.left || !v.right) { // v has 1 child if (v === this.root) { // v is root, assign the value of u to v, and delete u v.data = u.data; v.left = v.right = null; } else { // Detach v from tree and move u up if (v.isOnLeft()) parent.left = u; else parent.right = u; u.parent = parent; if (uvBlack) this.fixDoubleBlack(u); // u and v both black, fix double black at u else u.color = 1; // u or v red, color u black } return; } // v has 2 children, swap data with successor and recurse this.swapData(u, v); this.deleteNode(u); // find node that replaces a deleted node in BST function BSTreplace(x: RBTreeNode<T>): RBTreeNode<T> | null { // when node have 2 children if (x.left && x.right) return successor(x.right); // when leaf if (!x.left && !x.right) return null; // when single child return x.left ?? x.right; } // find node that do not have a left child // in the subtree of the given node function successor(x: RBTreeNode<T>): RBTreeNode<T> { let temp = x; while (temp.left) temp = temp.left; return temp; } } fixDoubleBlack(x: RBTreeNode<T>): void { if (x === this.root) return; // Reached root const sibling = x.sibling(); const parent = x.parent!; if (!sibling) { // No sibiling, double black pushed up this.fixDoubleBlack(parent); } else { if (sibling.color === 0) { // Sibling red parent.color = 0; sibling.color = 1; if (sibling.isOnLeft()) this.rotateRight(parent); // left case else this.rotateLeft(parent); // right case this.fixDoubleBlack(x); } else { // Sibling black if (sibling.hasRedChild()) { // at least 1 red children if (sibling.left && sibling.left.color === 0) { if (sibling.isOnLeft()) { // left left sibling.left.color = sibling.color; sibling.color = parent.color; this.rotateRight(parent); } else { // right left sibling.left.color = parent.color; this.rotateRight(sibling); this.rotateLeft(parent); } } else { if (sibling.isOnLeft()) { // left right sibling.right!.color = parent.color; this.rotateLeft(sibling); this.rotateRight(parent); } else { // right right sibling.right!.color = sibling.color; sibling.color = parent.color; this.rotateLeft(parent); } } parent.color = 1; } else { // 2 black children sibling.color = 0; if (parent.color === 1) this.fixDoubleBlack(parent); else parent.color = 1; } } } } insert(data: T): boolean { // search for a position to insert let parent = this.root; while (parent) { if (this.lt(data, parent.data)) { if (!parent.left) break; else parent = parent.left; } else if (this.lt(parent.data, data)) { if (!parent.right) break; else parent = parent.right; } else break; } // insert node into parent const node = new RBTreeNode(data); if (!parent) this.root = node; else if (this.lt(node.data, parent.data)) parent.left = node; else if (this.lt(parent.data, node.data)) parent.right = node; else { parent.count++; return false; } node.parent = parent; this.fixAfterInsert(node); return true; } find(data: T): RBTreeNode<T> | null { let p = this.root; while (p) { if (this.lt(data, p.data)) { p = p.left; } else if (this.lt(p.data, data)) { p = p.right; } else break; } return p ?? null; } *inOrder(root: RBTreeNode<T> = this.root!): Generator<T, undefined, void> { if (!root) return; for (const v of this.inOrder(root.left!)) yield v; yield root.data; for (const v of this.inOrder(root.right!)) yield v; } *reverseInOrder(root: RBTreeNode<T> = this.root!): Generator<T, undefined, void> { if (!root) return; for (const v of this.reverseInOrder(root.right!)) yield v; yield root.data; for (const v of this.reverseInOrder(root.left!)) yield v; } } class TreeSet<T = number> { _size: number; tree: RBTree<T>; compare: Compare<T>; constructor( collection: T[] | Compare<T> = [], compare: Compare<T> = (l: T, r: T) => (l < r ? -1 : l > r ? 1 : 0), ) { if (typeof collection === 'function') { compare = collection; collection = []; } this._size = 0; this.compare = compare; this.tree = new RBTree(compare); for (const val of collection) this.add(val); } size(): number { return this._size; } has(val: T): boolean { return !!this.tree.find(val); } add(val: T): boolean { const successful = this.tree.insert(val); this._size += successful ? 1 : 0; return successful; } delete(val: T): boolean { const deleted = this.tree.deleteAll(val); this._size -= deleted ? 1 : 0; return deleted; } ceil(val: T): T | undefined { let p = this.tree.root; let higher = null; while (p) { if (this.compare(p.data, val) >= 0) { higher = p; p = p.left; } else { p = p.right; } } return higher?.data; } floor(val: T): T | undefined { let p = this.tree.root; let lower = null; while (p) { if (this.compare(val, p.data) >= 0) { lower = p; p = p.right; } else { p = p.left; } } return lower?.data; } higher(val: T): T | undefined { let p = this.tree.root; let higher = null; while (p) { if (this.compare(val, p.data) < 0) { higher = p; p = p.left; } else { p = p.right; } } return higher?.data; } lower(val: T): T | undefined { let p = this.tree.root; let lower = null; while (p) { if (this.compare(p.data, val) < 0) { lower = p; p = p.right; } else { p = p.left; } } return lower?.data; } first(): T | undefined { return this.tree.inOrder().next().value; } last(): T | undefined { return this.tree.reverseInOrder().next().value; } shift(): T | undefined { const first = this.first(); if (first === undefined) return undefined; this.delete(first); return first; } pop(): T | undefined { const last = this.last(); if (last === undefined) return undefined; this.delete(last); return last; } *[Symbol.iterator](): Generator<T, void, void> { for (const val of this.values()) yield val; } *keys(): Generator<T, void, void> { for (const val of this.values()) yield val; } *values(): Generator<T, undefined, void> { for (const val of this.tree.inOrder()) yield val; return undefined; } /** * Return a generator for reverse order traversing the set */ *rvalues(): Generator<T, undefined, void> { for (const val of this.tree.reverseInOrder()) yield val; return undefined; } } class TreeMultiSet<T = number> { _size: number; tree: RBTree<T>; compare: Compare<T>; constructor( collection: T[] | Compare<T> = [], compare: Compare<T> = (l: T, r: T) => (l < r ? -1 : l > r ? 1 : 0), ) { if (typeof collection === 'function') { compare = collection; collection = []; } this._size = 0; this.compare = compare; this.tree = new RBTree(compare); for (const val of collection) this.add(val); } size(): number { return this._size; } has(val: T): boolean { return !!this.tree.find(val); } add(val: T): boolean { const successful = this.tree.insert(val); this._size++; return successful; } delete(val: T): boolean { const successful = this.tree.delete(val); if (!successful) return false; this._size--; return true; } count(val: T): number { const node = this.tree.find(val); return node ? node.count : 0; } ceil(val: T): T | undefined { let p = this.tree.root; let higher = null; while (p) { if (this.compare(p.data, val) >= 0) { higher = p; p = p.left; } else { p = p.right; } } return higher?.data; } floor(val: T): T | undefined { let p = this.tree.root; let lower = null; while (p) { if (this.compare(val, p.data) >= 0) { lower = p; p = p.right; } else { p = p.left; } } return lower?.data; } higher(val: T): T | undefined { let p = this.tree.root; let higher = null; while (p) { if (this.compare(val, p.data) < 0) { higher = p; p = p.left; } else { p = p.right; } } return higher?.data; } lower(val: T): T | undefined { let p = this.tree.root; let lower = null; while (p) { if (this.compare(p.data, val) < 0) { lower = p; p = p.right; } else { p = p.left; } } return lower?.data; } first(): T | undefined { return this.tree.inOrder().next().value; } last(): T | undefined { return this.tree.reverseInOrder().next().value; } shift(): T | undefined { const first = this.first(); if (first === undefined) return undefined; this.delete(first); return first; } pop(): T | undefined { const last = this.last(); if (last === undefined) return undefined; this.delete(last); return last; } *[Symbol.iterator](): Generator<T, void, void> { yield* this.values(); } *keys(): Generator<T, void, void> { for (const val of this.values()) yield val; } *values(): Generator<T, undefined, void> { for (const val of this.tree.inOrder()) { let count = this.count(val); while (count--) yield val; } return undefined; } /** * Return a generator for reverse order traversing the multi-set */ *rvalues(): Generator<T, undefined, void> { for (const val of this.tree.reverseInOrder()) { let count = this.count(val); while (count--) yield val; } return undefined; } }