Welcome to Subscribe On Youtube
149. Max Points on a Line
Description
Given an array of points where points[i] = [xi, yi] represents a point on the X-Y plane, return the maximum number of points that lie on the same straight line.
Example 1:

Input: points = [[1,1],[2,2],[3,3]] Output: 3
Example 2:
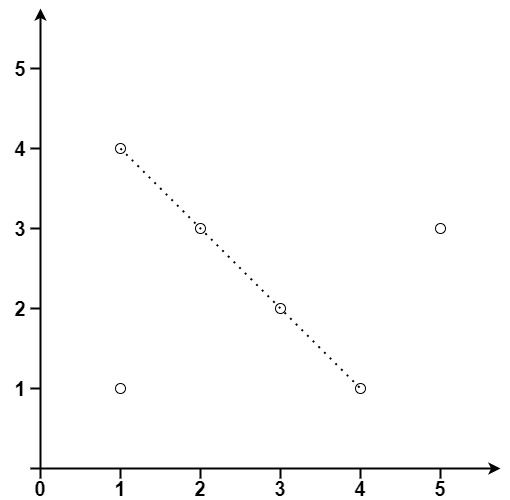
Input: points = [[1,1],[3,2],[5,3],[4,1],[2,3],[1,4]] Output: 4
Constraints:
1 <= points.length <= 300points[i].length == 2-104 <= xi, yi <= 104- All the
pointsare unique.
Solutions
-
class Solution { public int maxPoints(int[][] points) { int n = points.length; int ans = 1; for (int i = 0; i < n; ++i) { int x1 = points[i][0], y1 = points[i][1]; Map<String, Integer> cnt = new HashMap<>(); for (int j = i + 1; j < n; ++j) { int x2 = points[j][0], y2 = points[j][1]; int dx = x2 - x1, dy = y2 - y1; int g = gcd(dx, dy); String k = (dx / g) + "." + (dy / g); cnt.put(k, cnt.getOrDefault(k, 0) + 1); ans = Math.max(ans, cnt.get(k) + 1); } } return ans; } private int gcd(int a, int b) { return b == 0 ? a : gcd(b, a % b); } } -
class Solution { public: int gcd(int a, int b) { return b == 0 ? a : gcd(b, a % b); } int maxPoints(vector<vector<int>>& points) { int n = points.size(); int ans = 1; for (int i = 0; i < n; ++i) { int x1 = points[i][0], y1 = points[i][1]; unordered_map<string, int> cnt; for (int j = i + 1; j < n; ++j) { int x2 = points[j][0], y2 = points[j][1]; int dx = x2 - x1, dy = y2 - y1; int g = gcd(dx, dy); string k = to_string(dx / g) + "." + to_string(dy / g); cnt[k]++; ans = max(ans, cnt[k] + 1); } } return ans; } }; -
class Solution: def maxPoints(self, points: List[List[int]]) -> int: def gcd(a, b): return a if b == 0 else gcd(b, a % b) n = len(points) ans = 1 for i in range(n): x1, y1 = points[i] cnt = Counter() for j in range(i + 1, n): x2, y2 = points[j] dx, dy = x2 - x1, y2 - y1 g = gcd(dx, dy) k = (dx // g, dy // g) cnt[k] += 1 ans = max(ans, cnt[k] + 1) return ans -
func maxPoints(points [][]int) int { n := len(points) ans := 1 type pair struct{ x, y int } for i := 0; i < n; i++ { x1, y1 := points[i][0], points[i][1] cnt := map[pair]int{} for j := i + 1; j < n; j++ { x2, y2 := points[j][0], points[j][1] dx, dy := x2-x1, y2-y1 g := gcd(dx, dy) k := pair{dx / g, dy / g} cnt[k]++ if ans < cnt[k]+1 { ans = cnt[k] + 1 } } } return ans } func gcd(a, b int) int { if b == 0 { return a } return gcd(b, a%b) } -
public class Solution { public int MaxPoints(int[][] points) { int n = points.Length; int ans = 1; for (int i = 0; i < n; ++i) { int x1 = points[i][0], y1 = points[i][1]; for (int j = i + 1; j < n; ++j) { int x2 = points[j][0], y2 = points[j][1]; int cnt = 2; for (int k = j + 1; k < n; ++k) { int x3 = points[k][0], y3 = points[k][1]; int a = (y2 - y1) * (x3 - x1); int b = (y3 - y1) * (x2 - x1); if (a == b) { ++cnt; } } if (ans < cnt) { ans = cnt; } } } return ans; } }