Welcome to Subscribe On Youtube
3243. Shortest Distance After Road Addition Queries I
Description
You are given an integer n and a 2D integer array queries.
There are n cities numbered from 0 to n - 1. Initially, there is a unidirectional road from city i to city i + 1 for all 0 <= i < n - 1.
queries[i] = [ui, vi] represents the addition of a new unidirectional road from city ui to city vi. After each query, you need to find the length of the shortest path from city 0 to city n - 1.
Return an array answer where for each i in the range [0, queries.length - 1], answer[i] is the length of the shortest path from city 0 to city n - 1 after processing the first i + 1 queries.
Example 1:
Input: n = 5, queries = [[2,4],[0,2],[0,4]]
Output: [3,2,1]
Explanation:

After the addition of the road from 2 to 4, the length of the shortest path from 0 to 4 is 3.

After the addition of the road from 0 to 2, the length of the shortest path from 0 to 4 is 2.
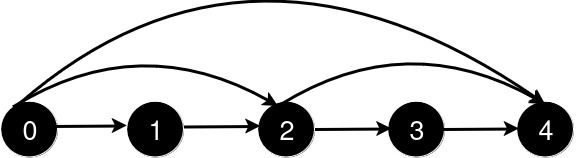
After the addition of the road from 0 to 4, the length of the shortest path from 0 to 4 is 1.
Example 2:
Input: n = 4, queries = [[0,3],[0,2]]
Output: [1,1]
Explanation:
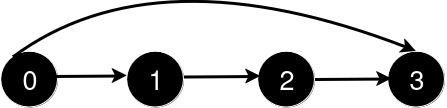
After the addition of the road from 0 to 3, the length of the shortest path from 0 to 3 is 1.
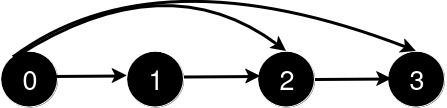
After the addition of the road from 0 to 2, the length of the shortest path remains 1.
Constraints:
3 <= n <= 5001 <= queries.length <= 500queries[i].length == 20 <= queries[i][0] < queries[i][1] < n1 < queries[i][1] - queries[i][0]- There are no repeated roads among the queries.
Solutions
Solution 1: BFS
First, we establish a directed graph $\textit{g}$, where $\textit{g}[i]$ represents the list of cities that can be reached from city $i$. Initially, each city $i$ has a one-way road leading to city $i + 1$.
Then, for each query $[u, v]$, we add $u$ to the departure city list of $v$, and then use BFS to find the shortest path length from city $0$ to city $n - 1$, adding the result to the answer array.
Finally, we return the answer array.
Time complexity is $O(q \times (n + q))$, and space complexity is $O(n + q)$. Here, $n$ and $q$ are the number of cities and the number of queries, respectively.
-
class Solution { private List<Integer>[] g; private int n; public int[] shortestDistanceAfterQueries(int n, int[][] queries) { this.n = n; g = new List[n]; Arrays.setAll(g, i -> new ArrayList<>()); for (int i = 0; i < n - 1; ++i) { g[i].add(i + 1); } int m = queries.length; int[] ans = new int[m]; for (int i = 0; i < m; ++i) { int u = queries[i][0], v = queries[i][1]; g[u].add(v); ans[i] = bfs(0); } return ans; } private int bfs(int i) { Deque<Integer> q = new ArrayDeque<>(); q.offer(i); boolean[] vis = new boolean[n]; vis[i] = true; for (int d = 0;; ++d) { for (int k = q.size(); k > 0; --k) { int u = q.poll(); if (u == n - 1) { return d; } for (int v : g[u]) { if (!vis[v]) { vis[v] = true; q.offer(v); } } } } } } -
class Solution { public: vector<int> shortestDistanceAfterQueries(int n, vector<vector<int>>& queries) { vector<int> g[n]; for (int i = 0; i < n - 1; ++i) { g[i].push_back(i + 1); } auto bfs = [&](int i) -> int { queue<int> q{ {i} }; vector<bool> vis(n); vis[i] = true; for (int d = 0;; ++d) { for (int k = q.size(); k; --k) { int u = q.front(); q.pop(); if (u == n - 1) { return d; } for (int v : g[u]) { if (!vis[v]) { vis[v] = true; q.push(v); } } } } }; vector<int> ans; for (const auto& q : queries) { g[q[0]].push_back(q[1]); ans.push_back(bfs(0)); } return ans; } }; -
class Solution: def shortestDistanceAfterQueries( self, n: int, queries: List[List[int]] ) -> List[int]: def bfs(i: int) -> int: q = deque([i]) vis = [False] * n vis[i] = True d = 0 while 1: for _ in range(len(q)): u = q.popleft() if u == n - 1: return d for v in g[u]: if not vis[v]: vis[v] = True q.append(v) d += 1 g = [[i + 1] for i in range(n - 1)] ans = [] for u, v in queries: g[u].append(v) ans.append(bfs(0)) return ans -
func shortestDistanceAfterQueries(n int, queries [][]int) []int { g := make([][]int, n) for i := range g { g[i] = append(g[i], i+1) } bfs := func(i int) int { q := []int{i} vis := make([]bool, n) vis[i] = true for d := 0; ; d++ { for k := len(q); k > 0; k-- { u := q[0] if u == n-1 { return d } q = q[1:] for _, v := range g[u] { if !vis[v] { vis[v] = true q = append(q, v) } } } } } ans := make([]int, len(queries)) for i, q := range queries { g[q[0]] = append(g[q[0]], q[1]) ans[i] = bfs(0) } return ans } -
function shortestDistanceAfterQueries(n: number, queries: number[][]): number[] { const g: number[][] = Array.from({ length: n }, () => []); for (let i = 0; i < n - 1; ++i) { g[i].push(i + 1); } const bfs = (i: number): number => { const q: number[] = [i]; const vis: boolean[] = Array(n).fill(false); vis[i] = true; for (let d = 0; ; ++d) { const nq: number[] = []; for (const u of q) { if (u === n - 1) { return d; } for (const v of g[u]) { if (!vis[v]) { vis[v] = true; nq.push(v); } } } q.splice(0, q.length, ...nq); } }; const ans: number[] = []; for (const [u, v] of queries) { g[u].push(v); ans.push(bfs(0)); } return ans; }