Welcome to Subscribe On Youtube
3067. Count Pairs of Connectable Servers in a Weighted Tree Network
Description
You are given an unrooted weighted tree with n vertices representing servers numbered from 0 to n - 1, an array edges where edges[i] = [ai, bi, weighti] represents a bidirectional edge between vertices ai and bi of weight weighti. You are also given an integer signalSpeed.
Two servers a and b are connectable through a server c if:
a < b,a != candb != c.- The distance from
ctoais divisible bysignalSpeed. - The distance from
ctobis divisible bysignalSpeed. - The path from
ctoband the path fromctoado not share any edges.
Return an integer array count of length n where count[i] is the number of server pairs that are connectable through the server i.
Example 1:
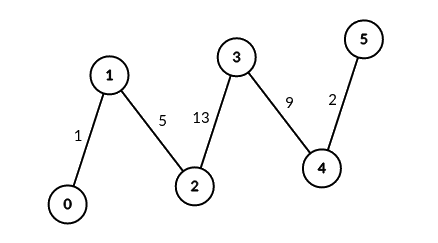
Input: edges = [[0,1,1],[1,2,5],[2,3,13],[3,4,9],[4,5,2]], signalSpeed = 1 Output: [0,4,6,6,4,0] Explanation: Since signalSpeed is 1, count[c] is equal to the number of pairs of paths that start at c and do not share any edges. In the case of the given path graph, count[c] is equal to the number of servers to the left of c multiplied by the servers to the right of c.
Example 2:
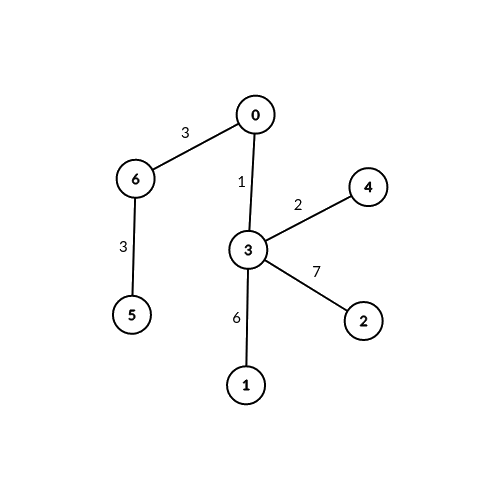
Input: edges = [[0,6,3],[6,5,3],[0,3,1],[3,2,7],[3,1,6],[3,4,2]], signalSpeed = 3 Output: [2,0,0,0,0,0,2] Explanation: Through server 0, there are 2 pairs of connectable servers: (4, 5) and (4, 6). Through server 6, there are 2 pairs of connectable servers: (4, 5) and (0, 5). It can be shown that no two servers are connectable through servers other than 0 and 6.
Constraints:
2 <= n <= 1000edges.length == n - 1edges[i].length == 30 <= ai, bi < nedges[i] = [ai, bi, weighti]1 <= weighti <= 1061 <= signalSpeed <= 106- The input is generated such that
edgesrepresents a valid tree.
Solutions
Solution 1: Enumeration + DFS
First, we construct an adjacency list g based on the edges given in the problem, where g[a] represents all the neighbor nodes of node a and their corresponding edge weights.
Then, we can enumerate each node a as the connecting intermediate node, and calculate the number of nodes t that start from the neighbor node b of a and whose distance to node a can be divided by signalSpeed through depth-first search. Then, the number of connectable node pairs of node a increases by s * t, where s represents the cumulative number of nodes that start from the neighbor node b of a and whose distance to node a cannot be divided by signalSpeed. Then we update s to s + t.
After enumerating all nodes a, we can get the number of connectable node pairs for all nodes.
The time complexity is $O(n^2)$, and the space complexity is $O(n)$, where $n$ is the number of nodes.
-
class Solution { private int signalSpeed; private List<int[]>[] g; public int[] countPairsOfConnectableServers(int[][] edges, int signalSpeed) { int n = edges.length + 1; g = new List[n]; this.signalSpeed = signalSpeed; Arrays.setAll(g, k -> new ArrayList<>()); for (var e : edges) { int a = e[0], b = e[1], w = e[2]; g[a].add(new int[] {b, w}); g[b].add(new int[] {a, w}); } int[] ans = new int[n]; for (int a = 0; a < n; ++a) { int s = 0; for (var e : g[a]) { int b = e[0], w = e[1]; int t = dfs(b, a, w); ans[a] += s * t; s += t; } } return ans; } private int dfs(int a, int fa, int ws) { int cnt = ws % signalSpeed == 0 ? 1 : 0; for (var e : g[a]) { int b = e[0], w = e[1]; if (b != fa) { cnt += dfs(b, a, ws + w); } } return cnt; } } -
class Solution { public: vector<int> countPairsOfConnectableServers(vector<vector<int>>& edges, int signalSpeed) { int n = edges.size() + 1; vector<pair<int, int>> g[n]; for (auto& e : edges) { int a = e[0], b = e[1], w = e[2]; g[a].emplace_back(b, w); g[b].emplace_back(a, w); } function<int(int, int, int)> dfs = [&](int a, int fa, int ws) { int cnt = ws % signalSpeed == 0; for (auto& [b, w] : g[a]) { if (b != fa) { cnt += dfs(b, a, ws + w); } } return cnt; }; vector<int> ans(n); for (int a = 0; a < n; ++a) { int s = 0; for (auto& [b, w] : g[a]) { int t = dfs(b, a, w); ans[a] += s * t; s += t; } } return ans; } }; -
class Solution: def countPairsOfConnectableServers( self, edges: List[List[int]], signalSpeed: int ) -> List[int]: def dfs(a: int, fa: int, ws: int) -> int: cnt = 0 if ws % signalSpeed else 1 for b, w in g[a]: if b != fa: cnt += dfs(b, a, ws + w) return cnt n = len(edges) + 1 g = [[] for _ in range(n)] for a, b, w in edges: g[a].append((b, w)) g[b].append((a, w)) ans = [0] * n for a in range(n): s = 0 for b, w in g[a]: t = dfs(b, a, w) ans[a] += s * t s += t return ans -
func countPairsOfConnectableServers(edges [][]int, signalSpeed int) []int { n := len(edges) + 1 type pair struct{ x, w int } g := make([][]pair, n) for _, e := range edges { a, b, w := e[0], e[1], e[2] g[a] = append(g[a], pair{b, w}) g[b] = append(g[b], pair{a, w}) } var dfs func(a, fa, ws int) int dfs = func(a, fa, ws int) int { cnt := 0 if ws%signalSpeed == 0 { cnt++ } for _, e := range g[a] { b, w := e.x, e.w if b != fa { cnt += dfs(b, a, ws+w) } } return cnt } ans := make([]int, n) for a := 0; a < n; a++ { s := 0 for _, e := range g[a] { b, w := e.x, e.w t := dfs(b, a, w) ans[a] += s * t s += t } } return ans } -
function countPairsOfConnectableServers(edges: number[][], signalSpeed: number): number[] { const n = edges.length + 1; const g: [number, number][][] = Array.from({ length: n }, () => []); for (const [a, b, w] of edges) { g[a].push([b, w]); g[b].push([a, w]); } const dfs = (a: number, fa: number, ws: number): number => { let cnt = ws % signalSpeed === 0 ? 1 : 0; for (const [b, w] of g[a]) { if (b != fa) { cnt += dfs(b, a, ws + w); } } return cnt; }; const ans: number[] = Array(n).fill(0); for (let a = 0; a < n; ++a) { let s = 0; for (const [b, w] of g[a]) { const t = dfs(b, a, w); ans[a] += s * t; s += t; } } return ans; }