Welcome to Subscribe On Youtube
2950. Number of Divisible Substrings
Description
Each character of the English alphabet has been mapped to a digit as shown below.
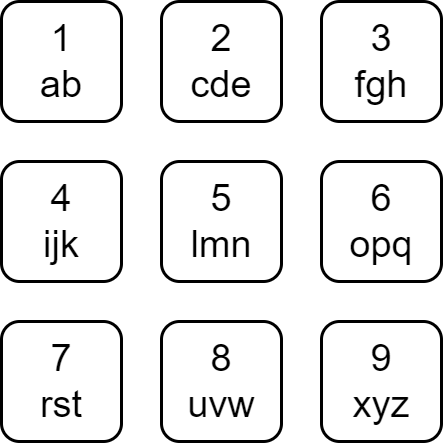
A string is divisible if the sum of the mapped values of its characters is divisible by its length.
Given a string s, return the number of divisible substrings of s.
A substring is a contiguous non-empty sequence of characters within a string.
Example 1:
| Substring | Mapped | Sum | Length | Divisible? |
|---|---|---|---|---|
| a | 1 | 1 | 1 | Yes |
| s | 7 | 7 | 1 | Yes |
| d | 2 | 2 | 1 | Yes |
| f | 3 | 3 | 1 | Yes |
| as | 1, 7 | 8 | 2 | Yes |
| sd | 7, 2 | 9 | 2 | No |
| df | 2, 3 | 5 | 2 | No |
| asd | 1, 7, 2 | 10 | 3 | No |
| sdf | 7, 2, 3 | 12 | 3 | Yes |
| asdf | 1, 7, 2, 3 | 13 | 4 | No |
Input: word = "asdf" Output: 6 Explanation: The table above contains the details about every substring of word, and we can see that 6 of them are divisible.
Example 2:
Input: word = "bdh" Output: 4 Explanation: The 4 divisible substrings are: "b", "d", "h", "bdh". It can be shown that there are no other substrings of word that are divisible.
Example 3:
Input: word = "abcd" Output: 6 Explanation: The 6 divisible substrings are: "a", "b", "c", "d", "ab", "cd". It can be shown that there are no other substrings of word that are divisible.
Constraints:
1 <= word.length <= 2000wordconsists only of lowercase English letters.
Solutions
Solution 1: Enumeration
First, we use a hash table or array $mp$ to record the number corresponding to each letter.
Then, we enumerate the starting position $i$ of the substring, and then enumerate the ending position $j$ of the substring, calculate the numerical sum $s$ of the substring $s[i..j]$. If $s$ can be divided by $j-i+1$, then a divisible substring is found, and the answer is increased by one.
After the enumeration is over, return the answer.
The time complexity is $O(n^2)$, and the space complexity is $O(C)$. Where $n$ is the length of the string $word$, and $C$ is the size of the character set, in this question $C=26$.
Solution 2: Hash Table + Prefix Sum + Enumeration
Similar to Solution 1, we first use a hash table or array $mp$ to record the number corresponding to each letter.
If the sum of the numbers in an integer subarray can be divided by its length, then the average value of this subarray must be an integer. And because the number of each element in the subarray is in the range of $[1, 9]$, the average value of the subarray can only be one of $1, 2, \cdots, 9$.
We can enumerate the average value $i$ of the subarray. If the sum of the elements in a subarray can be divided by $i$, suppose the subarray is $a_1, a_2, \cdots, a_k$, then $a_1 + a_2 + \cdots + a_k = i \times k$, that is, $(a_1 - i) + (a_2 - i) + \cdots + (a_k - i) = 0$. If we regard $a_k - i$ as a new element $b_k$, then the original subarray becomes $b_1, b_2, \cdots, b_k$, where $b_1 + b_2 + \cdots + b_k = 0$. We only need to find out how many subarrays in the new array have an element sum of $0$, which can be implemented with “hash table” combined with “prefix sum”.
The time complexity is $O(10 \times n)$, and the space complexity is $O(n)$. Here, $n$ is the length of the string $word$.
-
class Solution { public int countDivisibleSubstrings(String word) { String[] d = {"ab", "cde", "fgh", "ijk", "lmn", "opq", "rst", "uvw", "xyz"}; int[] mp = new int[26]; for (int i = 0; i < d.length; ++i) { for (char c : d[i].toCharArray()) { mp[c - 'a'] = i + 1; } } int ans = 0; int n = word.length(); for (int i = 0; i < n; ++i) { int s = 0; for (int j = i; j < n; ++j) { s += mp[word.charAt(j) - 'a']; ans += s % (j - i + 1) == 0 ? 1 : 0; } } return ans; } } -
class Solution { public: int countDivisibleSubstrings(string word) { string d[9] = {"ab", "cde", "fgh", "ijk", "lmn", "opq", "rst", "uvw", "xyz"}; int mp[26]{}; for (int i = 0; i < 9; ++i) { for (char& c : d[i]) { mp[c - 'a'] = i + 1; } } int ans = 0; int n = word.size(); for (int i = 0; i < n; ++i) { int s = 0; for (int j = i; j < n; ++j) { s += mp[word[j] - 'a']; ans += s % (j - i + 1) == 0 ? 1 : 0; } } return ans; } }; -
class Solution: def countDivisibleSubstrings(self, word: str) -> int: d = ["ab", "cde", "fgh", "ijk", "lmn", "opq", "rst", "uvw", "xyz"] mp = {} for i, s in enumerate(d, 1): for c in s: mp[c] = i ans = 0 n = len(word) for i in range(n): s = 0 for j in range(i, n): s += mp[word[j]] ans += s % (j - i + 1) == 0 return ans -
func countDivisibleSubstrings(word string) (ans int) { d := []string{"ab", "cde", "fgh", "ijk", "lmn", "opq", "rst", "uvw", "xyz"} mp := [26]int{} for i, s := range d { for _, c := range s { mp[c-'a'] = i + 1 } } n := len(word) for i := 0; i < n; i++ { s := 0 for j := i; j < n; j++ { s += mp[word[j]-'a'] if s%(j-i+1) == 0 { ans++ } } } return } -
function countDivisibleSubstrings(word: string): number { const d: string[] = ['ab', 'cde', 'fgh', 'ijk', 'lmn', 'opq', 'rst', 'uvw', 'xyz']; const mp: number[] = Array(26).fill(0); for (let i = 0; i < d.length; ++i) { for (const c of d[i]) { mp[c.charCodeAt(0) - 'a'.charCodeAt(0)] = i + 1; } } const n = word.length; let ans = 0; for (let i = 0; i < n; ++i) { let s = 0; for (let j = i; j < n; ++j) { s += mp[word.charCodeAt(j) - 'a'.charCodeAt(0)]; if (s % (j - i + 1) === 0) { ++ans; } } } return ans; } -
impl Solution { pub fn count_divisible_substrings(word: String) -> i32 { let d = vec!["ab", "cde", "fgh", "ijk", "lmn", "opq", "rst", "uvw", "xyz"]; let mut mp = vec![0; 26]; for (i, s) in d.iter().enumerate() { s.chars().for_each(|c| { mp[(c as usize) - ('a' as usize)] = (i + 1) as i32; }); } let mut ans = 0; let n = word.len(); for i in 0..n { let mut s = 0; for j in i..n { s += mp[(word.as_bytes()[j] as usize) - ('a' as usize)]; ans += (s % ((j - i + 1) as i32) == 0) as i32; } } ans } }