Welcome to Subscribe On Youtube

2791. Count Paths That Can Form a Palindrome in a Tree

Description

You are given a tree (i.e. a connected, undirected graph that has no cycles) rooted at node 0 consisting of n nodes numbered from 0 to n - 1. The tree is represented by a 0-indexed array parent of size n, where parent[i] is the parent of node i. Since node 0 is the root, parent[0] == -1.

You are also given a string s of length n, where s[i] is the character assigned to the edge between i and parent[i]. s[0] can be ignored.

Return the number of pairs of nodes (u, v) such that u < v and the characters assigned to edges on the path from u to v can be rearranged to form a palindrome.

A string is a palindrome when it reads the same backwards as forwards.

 

Example 1:

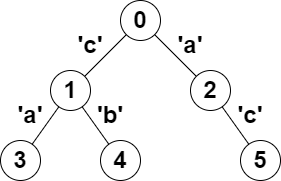
Input: parent = [-1,0,0,1,1,2], s = "acaabc"
Output: 8
Explanation: The valid pairs are:
- All the pairs (0,1), (0,2), (1,3), (1,4) and (2,5) result in one character which is always a palindrome.
- The pair (2,3) result in the string "aca" which is a palindrome.
- The pair (1,5) result in the string "cac" which is a palindrome.
- The pair (3,5) result in the string "acac" which can be rearranged into the palindrome "acca".

Example 2:

Input: parent = [-1,0,0,0,0], s = "aaaaa"
Output: 10
Explanation: Any pair of nodes (u,v) where u < v is valid.

 

Constraints:

• n == parent.length == s.length
• 1 <= n <= 105
• 0 <= parent[i] <= n - 1 for all i >= 1
• parent[0] == -1
• parent represents a valid tree.
• s consists of only lowercase English letters.

Solutions

• Java
• C++
• Python
• Go
• TypeScript

• class Solution {
      private List<int[]>[] g;
      private Map<Integer, Integer> cnt = new HashMap<>();
      private long ans;
  
      public long countPalindromePaths(List<Integer> parent, String s) {
          int n = parent.size();
          g = new List[n];
          cnt.put(0, 1);
          Arrays.setAll(g, k -> new ArrayList<>());
          for (int i = 1; i < n; ++i) {
              int p = parent.get(i);
              g[p].add(new int[] {i, 1 << (s.charAt(i) - 'a')});
          }
          dfs(0, 0);
          return ans;
      }
  
      private void dfs(int i, int xor) {
          for (int[] e : g[i]) {
              int j = e[0], v = e[1];
              int x = xor ^ v;
              ans += cnt.getOrDefault(x, 0);
              for (int k = 0; k < 26; ++k) {
                  ans += cnt.getOrDefault(x ^ (1 << k), 0);
              }
              cnt.merge(x, 1, Integer::sum);
              dfs(j, x);
          }
      }
  }
  

• class Solution {
  public:
      long long countPalindromePaths(vector<int>& parent, string s) {
          int n = parent.size();
          vector<vector<pair<int, int>>> g(n);
          unordered_map<int, int> cnt;
          cnt[0] = 1;
          for (int i = 1; i < n; ++i) {
              int p = parent[i];
              g[p].emplace_back(i, 1 << (s[i] - 'a'));
          }
          long long ans = 0;
          function<void(int, int)> dfs = [&](int i, int xo) {
              for (auto [j, v] : g[i]) {
                  int x = xo ^ v;
                  ans += cnt[x];
                  for (int k = 0; k < 26; ++k) {
                      ans += cnt[x ^ (1 << k)];
                  }
                  ++cnt[x];
                  dfs(j, x);
              }
          };
          dfs(0, 0);
          return ans;
      }
  };
  

• class Solution:
      def countPalindromePaths(self, parent: List[int], s: str) -> int:
          def dfs(i: int, xor: int):
              nonlocal ans
              for j, v in g[i]:
                  x = xor ^ v
                  ans += cnt[x]
                  for k in range(26):
                      ans += cnt[x ^ (1 << k)]
                  cnt[x] += 1
                  dfs(j, x)
  
          n = len(parent)
          g = defaultdict(list)
          for i in range(1, n):
              p = parent[i]
              g[p].append((i, 1 << (ord(s[i]) - ord('a'))))
          ans = 0
          cnt = Counter({0: 1})
          dfs(0, 0)
          return ans
  
  

• func countPalindromePaths(parent []int, s string) (ans int64) {
  	type pair struct{ i, v int }
  	n := len(parent)
  	g := make([][]pair, n)
  	for i := 1; i < n; i++ {
  		p := parent[i]
  		g[p] = append(g[p], pair{i, 1 << (s[i] - 'a')})
  	}
  	cnt := map[int]int{0: 1}
  	var dfs func(i, xor int)
  	dfs = func(i, xor int) {
  		for _, e := range g[i] {
  			x := xor ^ e.v
  			ans += int64(cnt[x])
  			for k := 0; k < 26; k++ {
  				ans += int64(cnt[x^(1<<k)])
  			}
  			cnt[x]++
  			dfs(e.i, x)
  		}
  	}
  	dfs(0, 0)
  	return
  }
  

• function countPalindromePaths(parent: number[], s: string): number {
      const n = parent.length;
      const g: [number, number][][] = Array.from({ length: n }, () => []);
      for (let i = 1; i < n; ++i) {
          g[parent[i]].push([i, 1 << (s.charCodeAt(i) - 97)]);
      }
      const cnt: Map<number, number> = new Map();
      cnt.set(0, 1);
      let ans = 0;
      const dfs = (i: number, xor: number): void => {
          for (const [j, v] of g[i]) {
              const x = xor ^ v;
              ans += cnt.get(x) || 0;
              for (let k = 0; k < 26; ++k) {
                  ans += cnt.get(x ^ (1 << k)) || 0;
              }
              cnt.set(x, (cnt.get(x) || 0) + 1);
              dfs(j, x);
          }
      };
      dfs(0, 0);
      return ans;
  }
  
  

All Problems

All Solutions