Formatted question description: https://leetcode.ca/all/2493.html

2493. Divide Nodes Into the Maximum Number of Groups

Difficulty: Hard.
Related Topics: .
Similar Questions: Binary Tree Level Order Traversal, Is Graph Bipartite?.

Problem

You are given a positive integer n representing the number of nodes in an undirected graph. The nodes are labeled from 1 to n.

You are also given a 2D integer array edges, where edges[i] = [ai, bi] indicates that there is a bidirectional edge between nodes ai and bi. Notice that the given graph may be disconnected.

Divide the nodes of the graph into m groups (1-indexed) such that:

Each node in the graph belongs to exactly one group.
For every pair of nodes in the graph that are connected by an edge [ai, bi], if ai belongs to the group with index x, and bi belongs to the group with index y, then |y - x| = 1.

Return the maximum number of groups (i.e., maximum **m) into which you can divide the nodes. Return -1 **if it is impossible to group the nodes with the given conditions.

Example 1:

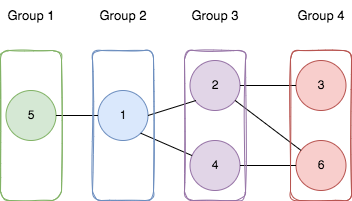
Input: n = 6, edges = [[1,2],[1,4],[1,5],[2,6],[2,3],[4,6]]
Output: 4
Explanation: As shown in the image we:
- Add node 5 to the first group.
- Add node 1 to the second group.
- Add nodes 2 and 4 to the third group.
- Add nodes 3 and 6 to the fourth group.
We can see that every edge is satisfied.
It can be shown that that if we create a fifth group and move any node from the third or fourth group to it, at least on of the edges will not be satisfied.

Example 2:

Input: n = 3, edges = [[1,2],[2,3],[3,1]]
Output: -1
Explanation: If we add node 1 to the first group, node 2 to the second group, and node 3 to the third group to satisfy the first two edges, we can see that the third edge will not be satisfied.
It can be shown that no grouping is possible.

Constraints:

1 <= n <= 500
1 <= edges.length <= 104
edges[i].length == 2
1 <= ai, bi <= n
ai != bi
There is at most one edge between any pair of vertices.

Solution (Java, C++, Python)

class Solution {
    private List<Integer>[] g;
    private List<Integer> arr = new ArrayList<>();
    private boolean[] vis;
    private int n;
    
    public int magnificentSets(int n, int[][] edges) {
        g = new List[n + 1];
        this.n = n;
        Arrays.setAll(g, k -> new ArrayList<>());
        for (var e : edges) {
            int a = e[0], b = e[1];
            g[a].add(b);
            g[b].add(a);
        }
        
        vis = new boolean[n + 1];
        int ans = 0;
        for (int i = 1; i <= n; ++i) {
            if (!vis[i]) {
                dfs(i);
                int t = -1;
                for (int v : arr) {
                    t = Math.max(t, bfs(v));
                }
                if (t == -1) {
                    return -1;
                }
                ans += t;
                arr.clear();
            }
        }
        return ans;
    }

    private int bfs(int k) {
        int[] dist = new int[n + 1];
        Arrays.fill(dist, 1 << 30);
        dist[k] = 1;
        Deque<Integer> q = new ArrayDeque<>();
        q.offer(k);
        int ans = 1;
        while (!q.isEmpty()) {
            int i = q.pollFirst();
            for (int j : g[i]) {
                if (dist[j] == 1 << 30) {
                    dist[j] = dist[i] + 1;
                    ans = dist[j];
                    q.offer(j);
                }
            }
        }
        for (int i : arr) {
            if (dist[i] == 1 << 30) {
                dist[i] = ++ans;
            }
        }
        for (int i : arr) {
            for (int j : g[i]) {
                if (Math.abs(dist[i] - dist[j]) != 1) {
                    return -1;
                }
            }
        }
        return ans;
    }

    private void dfs(int i) {
        arr.add(i);
        vis[i] = true;
        for (int j : g[i]) {
            if (!vis[j]) {
                dfs(j);
            }
        }
    }
}

class Solution {
public:
    int magnificentSets(int n, vector<vector<int>>& edges) {
        vector<vector<int>> g(n + 1);
        for (auto& e : edges) {
            int a = e[0], b = e[1];
            g[a].emplace_back(b);
            g[b].emplace_back(a);
        }
        vector<int> arr;
        bool vis[n + 1];
        memset(vis, 0, sizeof vis);
        int ans = 0;
        function<void(int)> dfs = [&](int i) {
            arr.emplace_back(i);
            vis[i] = true;
            for (int& j : g[i]) {
                if (!vis[j]) {
                    dfs(j);
                }
            }
        };
        auto bfs = [&](int k) {
            int ans = 1;
            int dist[n + 1];
            memset(dist, 0x3f, sizeof dist);
            dist[k] = 1;
            queue<int> q{ {k} };
            while (!q.empty()) {
                int i = q.front();
                q.pop();
                for (int& j : g[i]) {
                    if (dist[j] == 0x3f3f3f3f) {
                        ans = dist[j] = dist[i] + 1;
                        q.push(j);
                    }
                }
            }
            for (int& i : arr) {
                if (dist[i] == 0x3f3f3f3f) {
                    dist[i] = ++ans;
                }
            }
            for (int& i : arr) {
                for (int& j : g[i]) {
                    if (abs(dist[i] - dist[j]) != 1) {
                        return -1;
                    }
                }
            }
            return ans;
        };
        for (int i = 1; i <= n; ++i) {
            if (!vis[i]) {
                dfs(i);
                int t = -1;
                for (int& v : arr) t = max(t, bfs(v));
                if (t == -1) return -1;
                ans += t;
                arr.clear();
            }
        }
        return ans;
    }
};

class Solution:
    def magnificentSets(self, n: int, edges: List[List[int]]) -> int:
        def dfs(i):
            arr.append(i)
            vis[i] = True
            for j in g[i]:
                if not vis[j]:
                    dfs(j)

        def bfs(i):
            ans = 1
            dist = [inf] * (n + 1)
            dist[i] = 1
            q = deque([i])
            while q:
                i = q.popleft()
                for j in g[i]:
                    if dist[j] == inf:
                        ans = dist[j] = dist[i] + 1
                        q.append(j)
            for i in arr:
                if dist[i] == inf:
                    ans += 1
                    dist[i] = ans
            for i in arr:
                for j in g[i]:
                    if abs(dist[i] - dist[j]) != 1:
                        return -1
            return ans

        g = defaultdict(list)
        for a, b in edges:
            g[a].append(b)
            g[b].append(a)
        vis = [False] * (n + 1)
        ans = 0
        for i in range(1, n + 1):
            if not vis[i]:
                arr = []
                dfs(i)
                t = max(bfs(v) for v in arr)
                if t == -1:
                    return -1
                ans += t
        return ans

func magnificentSets(n int, edges [][]int) int {
	g := make([][]int, n+1)
	for _, e := range edges {
		a, b := e[0], e[1]
		g[a] = append(g[a], b)
		g[b] = append(g[b], a)
	}
	arr := []int{}
	vis := make([]bool, n+1)
	ans := 0
	var dfs func(int)
	dfs = func(i int) {
		arr = append(arr, i)
		vis[i] = true
		for _, j := range g[i] {
			if !vis[j] {
				dfs(j)
			}
		}
	}
	bfs := func(k int) int {
		ans := 1
		dist := make([]int, n+1)
		for i := range dist {
			dist[i] = 1 << 30
		}
		q := []int{k}
		dist[k] = 1
		for len(q) > 0 {
			i := q[0]
			q = q[1:]
			for _, j := range g[i] {
				if dist[j] == 1<<30 {
					dist[j] = dist[i] + 1
					ans = dist[j]
					q = append(q, j)
				}
			}
		}
		for _, i := range arr {
			if dist[i] == 1<<30 {
				ans++
				dist[i] = ans
			}
		}
		for _, i := range arr {
			for _, j := range g[i] {
				if abs(dist[i]-dist[j]) != 1 {
					return -1
				}
			}
		}
		return ans
	}
	for i := 1; i <= n; i++ {
		if !vis[i] {
			dfs(i)
			t := -1
			for _, v := range arr {
				t = max(t, bfs(v))
			}
			if t == -1 {
				return -1
			}
			ans += t
			arr = []int{}
		}
	}
	return ans
}

func max(a, b int) int {
	if a > b {
		return a
	}
	return b
}

func abs(x int) int {
	if x < 0 {
		return -x
	}
	return x
}

var magnificentSets = function (n, edges) {
    const graph = Array.from({ length: n + 1 }, () => new Set());
    for (const [u, v] of edges) {
        graph[u].add(v);
        graph[v].add(u);
    }
    const hash = new Map();

    // 2. BFS
    for (let i = 1; i <= n; i++) {
        let queue = [i];
        const dis = Array(n + 1).fill(0);
        dis[i] = 1;
        let mx = 1,
            mn = n;
        while (queue.length) {
            let next = [];
            for (let u of queue) {
                mn = Math.min(mn, u);
                for (const v of graph[u]) {
                    if (!dis[v]) {
                        dis[v] = dis[u] + 1;
                        mx = Math.max(mx, dis[v]);
                        next.push(v);
                    }
                    if (Math.abs(dis[u] - dis[v]) != 1) {
                        return -1;
                    }
                }
            }
            queue = next;
        }
        hash.set(mn, Math.max(mx, hash.get(mn) || 0));
    }

    let ans = 0;
    for (const [u, v] of hash) {
        ans += v;
    }
    return ans;
};

Explain:

nope.

Complexity:

Time complexity : O(n).
Space complexity : O(n).

2493 - Divide Nodes Into the Maximum Number of Groups

2493. Divide Nodes Into the Maximum Number of Groups

Problem

Solution (Java, C++, Python)

All Problems

All Solutions

Welcome to Subscribe On Youtube

2493. Divide Nodes Into the Maximum Number of Groups

Problem

Solution (Java, C++, Python)

All Problems

All Solutions