Formatted question description: https://leetcode.ca/all/2492.html

2492. Minimum Score of a Path Between Two Cities

Difficulty: Medium.
Related Topics: .
Similar Questions: Checking Existence of Edge Length Limited Paths, Checking Existence of Edge Length Limited Paths II.

Problem

You are given a positive integer n representing n cities numbered from 1 to n. You are also given a 2D array roads where roads[i] = [ai, bi, distancei] indicates that there is a **bidirectional **road between cities ai and bi with a distance equal to distancei. The cities graph is not necessarily connected.

The score of a path between two cities is defined as the **minimum **distance of a road in this path.

Return the **minimum **possible score of a path between cities **1 and **n.

Note:

A path is a sequence of roads between two cities.
It is allowed for a path to contain the same road multiple times, and you can visit cities 1 and n multiple times along the path.
The test cases are generated such that there is at least one path between 1 and n.

Example 1:

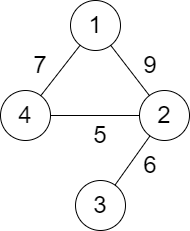
Input: n = 4, roads = [[1,2,9],[2,3,6],[2,4,5],[1,4,7]]
Output: 5
Explanation: The path from city 1 to 4 with the minimum score is: 1 -> 2 -> 4. The score of this path is min(9,5) = 5.
It can be shown that no other path has less score.

Example 2:

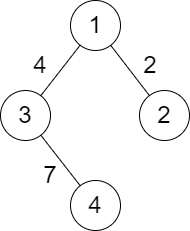
Input: n = 4, roads = [[1,2,2],[1,3,4],[3,4,7]]
Output: 2
Explanation: The path from city 1 to 4 with the minimum score is: 1 -> 2 -> 1 -> 3 -> 4. The score of this path is min(2,2,4,7) = 2.

Constraints:

2 <= n <= 105
1 <= roads.length <= 105
roads[i].length == 3
1 <= ai, bi <= n
ai != bi
1 <= distancei <= 104
There are no repeated edges.
There is at least one path between 1 and n.

Solution (Java, C++, Python)

class Solution {
    private List<int[]>[] g;
    private boolean[] vis;
    private int ans = 1 << 30;

    public int minScore(int n, int[][] roads) {
        g = new List[n];
        vis = new boolean[n];
        Arrays.setAll(g, k -> new ArrayList<>());
        for (var e : roads) {
            int a = e[0] - 1, b = e[1] - 1, d = e[2];
            g[a].add(new int[] {b, d});
            g[b].add(new int[] {a, d});
        }
        dfs(0);
        return ans;
    }

    private void dfs(int i) {
        for (var nxt : g[i]) {
            int j = nxt[0], d = nxt[1];
            ans = Math.min(ans, d);
            if (!vis[j]) {
                vis[j] = true;
                dfs(j);
            }
        }
    }
}

class Solution {
public:
    int minScore(int n, vector<vector<int>>& roads) {
        vector<vector<pair<int, int>>> g(n);
        bool vis[n];
        memset(vis, 0, sizeof vis);
        for (auto& e : roads) {
            int a = e[0] - 1, b = e[1] - 1, d = e[2];
            g[a].emplace_back(b, d);
            g[b].emplace_back(a, d);
        }
        int ans = INT_MAX;
        function<void(int)> dfs = [&](int i) {
            for (auto [j, d] : g[i]) {
                ans = min(ans, d);
                if (!vis[j]) {
                    vis[j] = true;
                    dfs(j);
                }
            }
        };
        dfs(0);
        return ans;
    }
};

class Solution:
    def minScore(self, n: int, roads: List[List[int]]) -> int:
        def dfs(i):
            nonlocal ans
            for j, d in g[i]:
                ans = min(ans, d)
                if not vis[j]:
                    vis[j] = True
                    dfs(j)

        g = defaultdict(list)
        for a, b, d in roads:
            g[a].append((b, d))
            g[b].append((a, d))
        vis = [False] * (n + 1)
        ans = inf
        dfs(1)
        return ans

func minScore(n int, roads [][]int) int {
	type pair struct{ i, v int }
	g := make([][]pair, n)
	for _, e := range roads {
		a, b, d := e[0]-1, e[1]-1, e[2]
		g[a] = append(g[a], pair{b, d})
		g[b] = append(g[b], pair{a, d})
	}
	vis := make([]bool, n)
	ans := 1 << 30
	var dfs func(int)
	dfs = func(i int) {
		for _, nxt := range g[i] {
			j, d := nxt.i, nxt.v
			ans = min(ans, d)
			if !vis[j] {
				vis[j] = true
				dfs(j)
			}
		}
	}
	dfs(0)
	return ans
}

func min(a, b int) int {
	if a < b {
		return a
	}
	return b
}

function minScore(n: number, roads: number[][]): number {
    const vis = new Array(n + 1).fill(false);
    const g = Array.from({ length: n + 1 }, () => []);
    for (const [a, b, v] of roads) {
        g[a].push([b, v]);
        g[b].push([a, v]);
    }
    let ans = Infinity;
    const dfs = (i: number) => {
        if (vis[i]) {
            return;
        }
        vis[i] = true;
        for (const [j, v] of g[i]) {
            ans = Math.min(ans, v);
            dfs(j);
        }
    };
    dfs(1);
    return ans;
}

var minScore = function (n, roads) {
    // 构建点到点的映射表
    const graph = Array.from({ length: n + 1 }, () => new Map());
    for (let [u, v, w] of roads) {
        graph[u].set(v, w);
        graph[v].set(u, w);
    }

    // DFS
    const vis = new Array(n).fill(false);
    let ans = Infinity;
    var dfs = function (u) {
        vis[u] = true;
        for (const [v, w] of graph[u]) {
            ans = Math.min(ans, w);
            if (!vis[v]) dfs(v);
        }
    };
    dfs(1);

    return ans;
};

impl Solution {
    fn dfs(i: usize, mut ans: i32, g: &Vec<Vec<(usize, i32)>>, vis: &mut Vec<bool>) -> i32 {
        if vis[i] {
            return ans;
        }
        vis[i] = true;
        for (j, v) in g[i].iter() {
            ans = ans.min(*v.min(&Self::dfs(*j, ans, g, vis)));
        }
        ans
    }

    pub fn min_score(n: i32, roads: Vec<Vec<i32>>) -> i32 {
        let n = n as usize;
        let mut vis = vec![false; n + 1];
        let mut g = vec![Vec::new(); n + 1];
        for road in roads.iter() {
            let a = road[0] as usize;
            let b = road[1] as usize;
            let v = road[2];
            g[a].push((b, v));
            g[b].push((a, v));
        }
        Self::dfs(1, i32::MAX, &g, &mut vis)
    }
}

Explain:

nope.

Complexity:

Time complexity : O(n).
Space complexity : O(n).

2492 - Minimum Score of a Path Between Two Cities

2492. Minimum Score of a Path Between Two Cities

Problem

Solution (Java, C++, Python)

All Problems

All Solutions

Welcome to Subscribe On Youtube

2492. Minimum Score of a Path Between Two Cities

Problem

Solution (Java, C++, Python)

All Problems

All Solutions