2477. Minimum Fuel Cost to Report to the Capital

Description

There is a tree (i.e., a connected, undirected graph with no cycles) structure country network consisting of n cities numbered from 0 to n - 1 and exactly n - 1 roads. The capital city is city 0. You are given a 2D integer array roads where roads[i] = [a_i, b_i] denotes that there exists a bidirectional road connecting cities a_i and b_i.

There is a meeting for the representatives of each city. The meeting is in the capital city.

There is a car in each city. You are given an integer seats that indicates the number of seats in each car.

A representative can use the car in their city to travel or change the car and ride with another representative. The cost of traveling between two cities is one liter of fuel.

Return the minimum number of liters of fuel to reach the capital city.

Example 1:

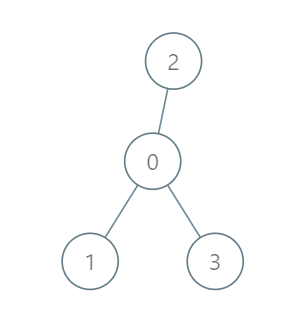
Input: roads = [[0,1],[0,2],[0,3]], seats = 5
Output: 3
Explanation: 
- Representative₁ goes directly to the capital with 1 liter of fuel.
- Representative₂ goes directly to the capital with 1 liter of fuel.
- Representative₃ goes directly to the capital with 1 liter of fuel.
It costs 3 liters of fuel at minimum. 
It can be proven that 3 is the minimum number of liters of fuel needed.

Example 2:

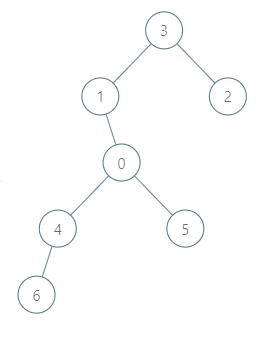
Input: roads = [[3,1],[3,2],[1,0],[0,4],[0,5],[4,6]], seats = 2
Output: 7
Explanation: 
- Representative₂ goes directly to city 3 with 1 liter of fuel.
- Representative₂ and representative₃ go together to city 1 with 1 liter of fuel.
- Representative₂ and representative₃ go together to the capital with 1 liter of fuel.
- Representative₁ goes directly to the capital with 1 liter of fuel.
- Representative₅ goes directly to the capital with 1 liter of fuel.
- Representative₆ goes directly to city 4 with 1 liter of fuel.
- Representative₄ and representative₆ go together to the capital with 1 liter of fuel.
It costs 7 liters of fuel at minimum. 
It can be proven that 7 is the minimum number of liters of fuel needed.

Example 3:

Input: roads = [], seats = 1
Output: 0
Explanation: No representatives need to travel to the capital city.

Constraints:

1 <= n <= 10⁵
roads.length == n - 1
roads[i].length == 2
0 <= a_i, b_i < n
a_i != b_i
roads represents a valid tree.
1 <= seats <= 10⁵

Solutions

Solution 1: Greedy + DFS

According to the problem description, we can find that all cars will only drive towards the capital (node $0$).

Suppose there is a node $a$, its next node is $b$, and node $a$ needs to pass through node $b$ to reach the capital. In order to make the vehicles (fuel consumption) of node $a$ as small as possible, we should greedily let the vehicles of the child nodes of node $a$ converge to node $a$ first, and then distribute the vehicles according to the number of seats $seats$. The minimum number of vehicles (fuel consumption) needed to reach node $b$ is $\lceil \frac{sz}{seats} \rceil$. Where $sz$ represents the number of nodes in the subtree with node $a$ as the root.

We start a depth-first search from node $0$, using a variable $sz$ to count the number of nodes in the subtree with the current node as the root. Initially, $sz = 1$, representing the current node itself. Then we traverse all the child nodes of the current node. For each child node $b$, we recursively calculate the number of nodes $t$ in the subtree with $b$ as the root, and add $t$ to $sz$, and then we add $\lceil \frac{t}{seats} \rceil$ to the answer. Finally, return $sz$.

The time complexity is $O(n)$, and the space complexity is $O(n)$. Here, $n$ is the number of nodes.

class Solution {
    private List<Integer>[] g;
    private int seats;
    private long ans;

    public long minimumFuelCost(int[][] roads, int seats) {
        int n = roads.length + 1;
        g = new List[n];
        Arrays.setAll(g, k -> new ArrayList<>());
        this.seats = seats;
        for (var e : roads) {
            int a = e[0], b = e[1];
            g[a].add(b);
            g[b].add(a);
        }
        dfs(0, -1);
        return ans;
    }

    private int dfs(int a, int fa) {
        int sz = 1;
        for (int b : g[a]) {
            if (b != fa) {
                int t = dfs(b, a);
                ans += (t + seats - 1) / seats;
                sz += t;
            }
        }
        return sz;
    }
}

class Solution {
public:
    long long minimumFuelCost(vector<vector<int>>& roads, int seats) {
        int n = roads.size() + 1;
        vector<int> g[n];
        for (auto& e : roads) {
            int a = e[0], b = e[1];
            g[a].emplace_back(b);
            g[b].emplace_back(a);
        }
        long long ans = 0;
        function<int(int, int)> dfs = [&](int a, int fa) {
            int sz = 1;
            for (int b : g[a]) {
                if (b != fa) {
                    int t = dfs(b, a);
                    ans += (t + seats - 1) / seats;
                    sz += t;
                }
            }
            return sz;
        };
        dfs(0, -1);
        return ans;
    }
};

class Solution:
    def minimumFuelCost(self, roads: List[List[int]], seats: int) -> int:
        def dfs(a: int, fa: int) -> int:
            nonlocal ans
            sz = 1
            for b in g[a]:
                if b != fa:
                    t = dfs(b, a)
                    ans += ceil(t / seats)
                    sz += t
            return sz

        g = defaultdict(list)
        for a, b in roads:
            g[a].append(b)
            g[b].append(a)
        ans = 0
        dfs(0, -1)
        return ans

func minimumFuelCost(roads [][]int, seats int) (ans int64) {
	n := len(roads) + 1
	g := make([][]int, n)
	for _, e := range roads {
		a, b := e[0], e[1]
		g[a] = append(g[a], b)
		g[b] = append(g[b], a)
	}
	var dfs func(int, int) int
	dfs = func(a, fa int) int {
		sz := 1
		for _, b := range g[a] {
			if b != fa {
				t := dfs(b, a)
				ans += int64((t + seats - 1) / seats)
				sz += t
			}
		}
		return sz
	}
	dfs(0, -1)
	return
}

function minimumFuelCost(roads: number[][], seats: number): number {
    const n = roads.length + 1;
    const g: number[][] = Array.from({ length: n }, () => []);
    for (const [a, b] of roads) {
        g[a].push(b);
        g[b].push(a);
    }
    let ans = 0;
    const dfs = (a: number, fa: number): number => {
        let sz = 1;
        for (const b of g[a]) {
            if (b !== fa) {
                const t = dfs(b, a);
                ans += Math.ceil(t / seats);
                sz += t;
            }
        }
        return sz;
    };
    dfs(0, -1);
    return ans;
}

impl Solution {
    pub fn minimum_fuel_cost(roads: Vec<Vec<i32>>, seats: i32) -> i64 {
        let n = roads.len() + 1;
        let mut g: Vec<Vec<usize>> = vec![vec![]; n];
        for road in roads.iter() {
            let a = road[0] as usize;
            let b = road[1] as usize;
            g[a].push(b);
            g[b].push(a);
        }
        let mut ans = 0;
        fn dfs(a: usize, fa: i32, g: &Vec<Vec<usize>>, ans: &mut i64, seats: i32) -> i32 {
            let mut sz = 1;
            for &b in g[a].iter() {
                if (b as i32) != fa {
                    let t = dfs(b, a as i32, g, ans, seats);
                    *ans += ((t + seats - 1) / seats) as i64;
                    sz += t;
                }
            }
            sz
        }
        dfs(0, -1, &g, &mut ans, seats);
        ans
    }
}

2477 - Minimum Fuel Cost to Report to the Capital

2477. Minimum Fuel Cost to Report to the Capital

Description

Solutions

All Problems

All Solutions

Welcome to Subscribe On Youtube

2477. Minimum Fuel Cost to Report to the Capital

Description

Solutions

All Problems

All Solutions