Welcome to Subscribe On Youtube
2473. Minimum Cost to Buy Apples
Description
You are given a positive integer n representing n cities numbered from 1 to n. You are also given a 2D array roads, where roads[i] = [ai, bi, costi] indicates that there is a bidirectional road between cities ai and bi with a cost of traveling equal to costi.
You can buy apples in any city you want, but some cities have different costs to buy apples. You are given the array appleCost where appleCost[i] is the cost of buying one apple from city i.
You start at some city, traverse through various roads, and eventually buy exactly one apple from any city. After you buy that apple, you have to return back to the city you started at, but now the cost of all the roads will be multiplied by a given factor k.
Given the integer k, return an array answer of size n where answer[i] is the minimum total cost to buy an apple if you start at city i.
Example 1:
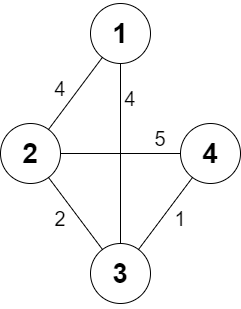
Input: n = 4, roads = [[1,2,4],[2,3,2],[2,4,5],[3,4,1],[1,3,4]], appleCost = [56,42,102,301], k = 2 Output: [54,42,48,51] Explanation: The minimum cost for each starting city is the following: - Starting at city 1: You take the path 1 -> 2, buy an apple at city 2, and finally take the path 2 -> 1. The total cost is 4 + 42 + 4 * 2 = 54. - Starting at city 2: You directly buy an apple at city 2. The total cost is 42. - Starting at city 3: You take the path 3 -> 2, buy an apple at city 2, and finally take the path 2 -> 3. The total cost is 2 + 42 + 2 * 2 = 48. - Starting at city 4: You take the path 4 -> 3 -> 2 then you buy at city 2, and finally take the path 2 -> 3 -> 4. The total cost is 1 + 2 + 42 + 1 * 2 + 2 * 2 = 51.
Example 2:
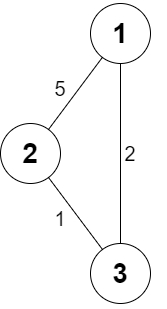
Input: n = 3, roads = [[1,2,5],[2,3,1],[3,1,2]], appleCost = [2,3,1], k = 3 Output: [2,3,1] Explanation: It is always optimal to buy the apple in the starting city.
Constraints:
2 <= n <= 10001 <= roads.length <= 10001 <= ai, bi <= nai != bi1 <= costi <= 105appleCost.length == n1 <= appleCost[i] <= 1051 <= k <= 100- There are no repeated edges.
Solutions
Solution 1: Heap-optimized Dijkstra’s Algorithm
We enumerate the starting point, and for each starting point, we use Dijkstra’s algorithm to find the shortest distance to all other points, and update the minimum value accordingly.
The time complexity is $O(n \times m \times \log m)$, where $n$ and $m$ are the number of cities and roads, respectively.
-
class Solution { private int k; private int[] cost; private int[] dist; private List<int[]>[] g; private static final int INF = 0x3f3f3f3f; public long[] minCost(int n, int[][] roads, int[] appleCost, int k) { cost = appleCost; g = new List[n]; dist = new int[n]; this.k = k; for (int i = 0; i < n; ++i) { g[i] = new ArrayList<>(); } for (var e : roads) { int a = e[0] - 1, b = e[1] - 1, c = e[2]; g[a].add(new int[] {b, c}); g[b].add(new int[] {a, c}); } long[] ans = new long[n]; for (int i = 0; i < n; ++i) { ans[i] = dijkstra(i); } return ans; } private long dijkstra(int u) { PriorityQueue<int[]> q = new PriorityQueue<>((a, b) -> a[0] - b[0]); q.offer(new int[] {0, u}); Arrays.fill(dist, INF); dist[u] = 0; long ans = Long.MAX_VALUE; while (!q.isEmpty()) { var p = q.poll(); int d = p[0]; u = p[1]; ans = Math.min(ans, cost[u] + (long) (k + 1) * d); for (var ne : g[u]) { int v = ne[0], w = ne[1]; if (dist[v] > dist[u] + w) { dist[v] = dist[u] + w; q.offer(new int[] {dist[v], v}); } } } return ans; } } -
using ll = long long; using pii = pair<int, int>; class Solution { public: const int inf = 0x3f3f3f3f; vector<long long> minCost(int n, vector<vector<int>>& roads, vector<int>& appleCost, int k) { vector<vector<pii>> g(n); for (auto& e : roads) { int a = e[0] - 1, b = e[1] - 1, c = e[2]; g[a].push_back({b, c}); g[b].push_back({a, c}); } int dist[n]; auto dijkstra = [&](int u) { memset(dist, 63, sizeof dist); priority_queue<pii, vector<pii>, greater<pii>> q; q.push({0, u}); dist[u] = 0; ll ans = LONG_MAX; while (!q.empty()) { auto p = q.top(); q.pop(); int d = p.first; u = p.second; ans = min(ans, appleCost[u] + 1ll * d * (k + 1)); for (auto& ne : g[u]) { auto [v, w] = ne; if (dist[v] > dist[u] + w) { dist[v] = dist[u] + w; q.push({dist[v], v}); } } } return ans; }; vector<ll> ans(n); for (int i = 0; i < n; ++i) ans[i] = dijkstra(i); return ans; } }; -
class Solution: def minCost( self, n: int, roads: List[List[int]], appleCost: List[int], k: int ) -> List[int]: def dijkstra(i): q = [(0, i)] dist = [inf] * n dist[i] = 0 ans = inf while q: d, u = heappop(q) ans = min(ans, appleCost[u] + d * (k + 1)) for v, w in g[u]: if dist[v] > dist[u] + w: dist[v] = dist[u] + w heappush(q, (dist[v], v)) return ans g = defaultdict(list) for a, b, c in roads: a, b = a - 1, b - 1 g[a].append((b, c)) g[b].append((a, c)) return [dijkstra(i) for i in range(n)] -
func minCost(n int, roads [][]int, appleCost []int, k int) []int64 { g := make([]pairs, n) for _, e := range roads { a, b, c := e[0]-1, e[1]-1, e[2] g[a] = append(g[a], pair{b, c}) g[b] = append(g[b], pair{a, c}) } const inf int = 0x3f3f3f3f dist := make([]int, n) dijkstra := func(u int) int64 { var ans int64 = math.MaxInt64 for i := range dist { dist[i] = inf } dist[u] = 0 q := make(pairs, 0) heap.Push(&q, pair{0, u}) for len(q) > 0 { p := heap.Pop(&q).(pair) d := p.first u = p.second ans = min(ans, int64(appleCost[u]+d*(k+1))) for _, ne := range g[u] { v, w := ne.first, ne.second if dist[v] > dist[u]+w { dist[v] = dist[u] + w heap.Push(&q, pair{dist[v], v}) } } } return ans } ans := make([]int64, n) for i := range ans { ans[i] = dijkstra(i) } return ans } type pair struct{ first, second int } var _ heap.Interface = (*pairs)(nil) type pairs []pair func (a pairs) Len() int { return len(a) } func (a pairs) Less(i int, j int) bool { return a[i].first < a[j].first || a[i].first == a[j].first && a[i].second < a[j].second } func (a pairs) Swap(i int, j int) { a[i], a[j] = a[j], a[i] } func (a *pairs) Push(x any) { *a = append(*a, x.(pair)) } func (a *pairs) Pop() any { l := len(*a); t := (*a)[l-1]; *a = (*a)[:l-1]; return t }