2471. Minimum Number of Operations to Sort a Binary Tree by Level

Description

You are given the root of a binary tree with unique values.

In one operation, you can choose any two nodes at the same level and swap their values.

Return the minimum number of operations needed to make the values at each level sorted in a strictly increasing order.

The level of a node is the number of edges along the path between it and the root node.

Example 1:

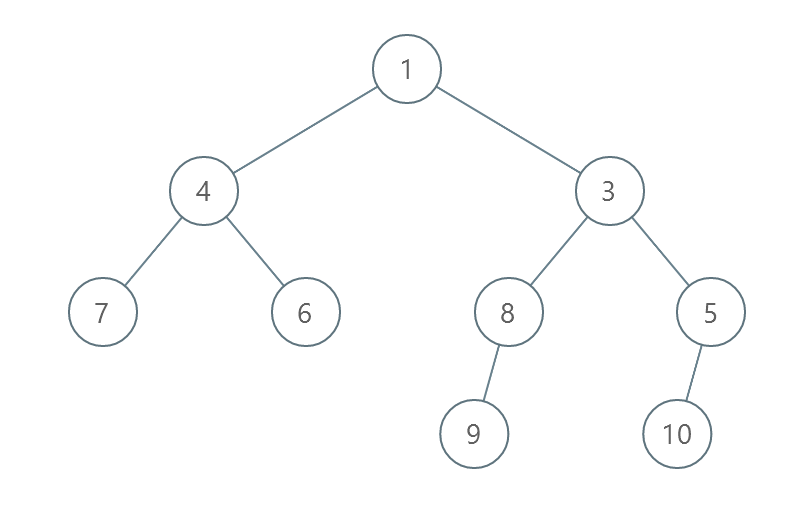
Input: root = [1,4,3,7,6,8,5,null,null,null,null,9,null,10]
Output: 3
Explanation:
- Swap 4 and 3. The 2^nd level becomes [3,4].
- Swap 7 and 5. The 3^rd level becomes [5,6,8,7].
- Swap 8 and 7. The 3^rd level becomes [5,6,7,8].
We used 3 operations so return 3.
It can be proven that 3 is the minimum number of operations needed.

Example 2:

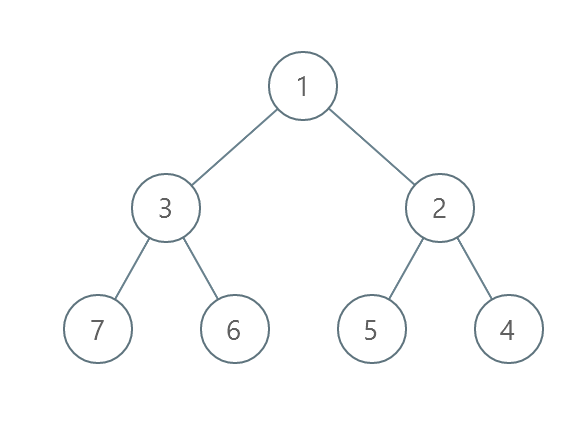
Input: root = [1,3,2,7,6,5,4]
Output: 3
Explanation:
- Swap 3 and 2. The 2^nd level becomes [2,3].
- Swap 7 and 4. The 3^rd level becomes [4,6,5,7].
- Swap 6 and 5. The 3^rd level becomes [4,5,6,7].
We used 3 operations so return 3.
It can be proven that 3 is the minimum number of operations needed.

Example 3:

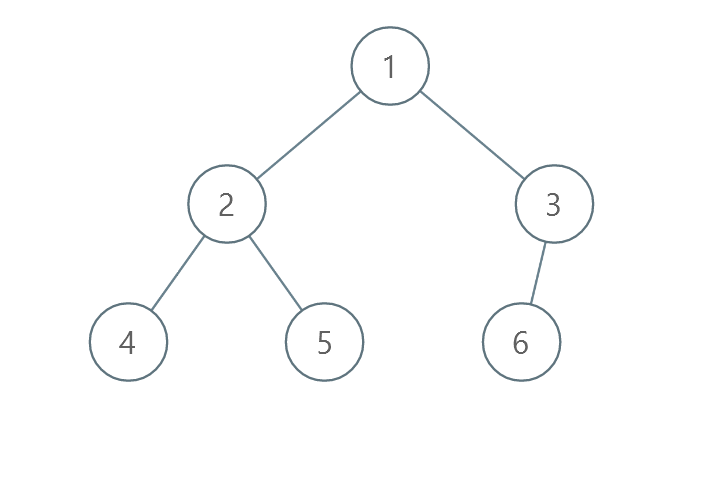
Input: root = [1,2,3,4,5,6]
Output: 0
Explanation: Each level is already sorted in increasing order so return 0.

Constraints:

The number of nodes in the tree is in the range [1, 10⁵].
1 <= Node.val <= 10⁵
All the values of the tree are unique.

Solutions

Solution 1: BFS + Discretization + Element Swap

First, we traverse the binary tree using BFS to find the node values at each level. Then, we sort the node values at each level. If the sorted node values are different from the original node values, it means that we need to swap elements. The number of swaps is the number of operations needed at that level.

The time complexity is $O(n \times \log n)$. Here, $n$ is the number of nodes in the binary tree.

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public int minimumOperations(TreeNode root) {
        Deque<TreeNode> q = new ArrayDeque<>();
        q.offer(root);
        int ans = 0;
        while (!q.isEmpty()) {
            List<Integer> t = new ArrayList<>();
            for (int n = q.size(); n > 0; --n) {
                TreeNode node = q.poll();
                t.add(node.val);
                if (node.left != null) {
                    q.offer(node.left);
                }
                if (node.right != null) {
                    q.offer(node.right);
                }
            }
            ans += f(t);
        }
        return ans;
    }

    private int f(List<Integer> t) {
        int n = t.size();
        List<Integer> alls = new ArrayList<>(t);
        alls.sort((a, b) -> a - b);
        Map<Integer, Integer> m = new HashMap<>();
        for (int i = 0; i < n; ++i) {
            m.put(alls.get(i), i);
        }
        int[] arr = new int[n];
        for (int i = 0; i < n; ++i) {
            arr[i] = m.get(t.get(i));
        }
        int ans = 0;
        for (int i = 0; i < n; ++i) {
            while (arr[i] != i) {
                swap(arr, i, arr[i]);
                ++ans;
            }
        }
        return ans;
    }

    private void swap(int[] arr, int i, int j) {
        int t = arr[i];
        arr[i] = arr[j];
        arr[j] = t;
    }
}

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int minimumOperations(TreeNode* root) {
        queue<TreeNode*> q{ {root} };
        int ans = 0;
        auto f = [](vector<int>& t) {
            int n = t.size();
            vector<int> alls(t.begin(), t.end());
            sort(alls.begin(), alls.end());
            unordered_map<int, int> m;
            int ans = 0;
            for (int i = 0; i < n; ++i) m[alls[i]] = i;
            for (int i = 0; i < n; ++i) t[i] = m[t[i]];
            for (int i = 0; i < n; ++i) {
                while (t[i] != i) {
                    swap(t[i], t[t[i]]);
                    ++ans;
                }
            }
            return ans;
        };
        while (!q.empty()) {
            vector<int> t;
            for (int n = q.size(); n; --n) {
                auto node = q.front();
                q.pop();
                t.emplace_back(node->val);
                if (node->left) q.push(node->left);
                if (node->right) q.push(node->right);
            }
            ans += f(t);
        }
        return ans;
    }
};

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def minimumOperations(self, root: Optional[TreeNode]) -> int:
        def swap(arr, i, j):
            arr[i], arr[j] = arr[j], arr[i]

        def f(t):
            n = len(t)
            m = {v: i for i, v in enumerate(sorted(t))}
            for i in range(n):
                t[i] = m[t[i]]
            ans = 0
            for i in range(n):
                while t[i] != i:
                    swap(t, i, t[i])
                    ans += 1
            return ans

        q = deque([root])
        ans = 0
        while q:
            t = []
            for _ in range(len(q)):
                node = q.popleft()
                t.append(node.val)
                if node.left:
                    q.append(node.left)
                if node.right:
                    q.append(node.right)
            ans += f(t)
        return ans

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func minimumOperations(root *TreeNode) (ans int) {
	f := func(t []int) int {
		var alls []int
		for _, v := range t {
			alls = append(alls, v)
		}
		sort.Ints(alls)
		m := make(map[int]int)
		for i, v := range alls {
			m[v] = i
		}
		for i := range t {
			t[i] = m[t[i]]
		}
		res := 0
		for i := range t {
			for t[i] != i {
				t[i], t[t[i]] = t[t[i]], t[i]
				res++
			}
		}
		return res
	}

	q := []*TreeNode{root}
	for len(q) > 0 {
		t := []int{}
		for n := len(q); n > 0; n-- {
			node := q[0]
			q = q[1:]
			t = append(t, node.Val)
			if node.Left != nil {
				q = append(q, node.Left)
			}
			if node.Right != nil {
				q = append(q, node.Right)
			}
		}
		ans += f(t)
	}
	return
}

/**
 * Definition for a binary tree node.
 * class TreeNode {
 *     val: number
 *     left: TreeNode | null
 *     right: TreeNode | null
 *     constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) {
 *         this.val = (val===undefined ? 0 : val)
 *         this.left = (left===undefined ? null : left)
 *         this.right = (right===undefined ? null : right)
 *     }
 * }
 */

function minimumOperations(root: TreeNode | null): number {
    const queue = [root];
    let ans = 0;
    while (queue.length !== 0) {
        const n = queue.length;
        const row: number[] = [];
        for (let i = 0; i < n; i++) {
            const { val, left, right } = queue.shift();
            row.push(val);
            left && queue.push(left);
            right && queue.push(right);
        }
        for (let i = 0; i < n - 1; i++) {
            let minIdx = i;
            for (let j = i + 1; j < n; j++) {
                if (row[j] < row[minIdx]) {
                    minIdx = j;
                }
            }
            if (i !== minIdx) {
                [row[i], row[minIdx]] = [row[minIdx], row[i]];
                ans++;
            }
        }
    }
    return ans;
}

// Definition for a binary tree node.
// #[derive(Debug, PartialEq, Eq)]
// pub struct TreeNode {
//   pub val: i32,
//   pub left: Option<Rc<RefCell<TreeNode>>>,
//   pub right: Option<Rc<RefCell<TreeNode>>>,
// }
//
// impl TreeNode {
//   #[inline]
//   pub fn new(val: i32) -> Self {
//     TreeNode {
//       val,
//       left: None,
//       right: None
//     }
//   }
// }
use std::rc::Rc;
use std::cell::RefCell;
use std::collections::VecDeque;
impl Solution {
    pub fn minimum_operations(root: Option<Rc<RefCell<TreeNode>>>) -> i32 {
        let mut queue = VecDeque::new();
        queue.push_back(root);
        let mut ans = 0;
        while !queue.is_empty() {
            let n = queue.len();
            let mut row = Vec::new();
            for _ in 0..n {
                let mut node = queue.pop_front().unwrap();
                let mut node = node.as_mut().unwrap().borrow_mut();
                row.push(node.val);
                if node.left.is_some() {
                    queue.push_back(node.left.take());
                }
                if node.right.is_some() {
                    queue.push_back(node.right.take());
                }
            }
            for i in 0..n - 1 {
                let mut min_idx = i;
                for j in i + 1..n {
                    if row[j] < row[min_idx] {
                        min_idx = j;
                    }
                }
                if i != min_idx {
                    row.swap(i, min_idx);
                    ans += 1;
                }
            }
        }
        ans
    }
}

2471 - Minimum Number of Operations to Sort a Binary Tree by Level

2471. Minimum Number of Operations to Sort a Binary Tree by Level

Description

Solutions

All Problems

All Solutions

Welcome to Subscribe On Youtube

2471. Minimum Number of Operations to Sort a Binary Tree by Level

Description

Solutions

All Problems

All Solutions