Welcome to Subscribe On Youtube
Formatted question description: https://leetcode.ca/all/2304.html
2304. Minimum Path Cost in a Grid
- Difficulty: Medium.
- Related Topics: Array, Dynamic Programming, Matrix.
- Similar Questions: Unique Paths, Unique Paths II, Minimum Path Sum, Dungeon Game, Paint House.
Problem
You are given a 0-indexed m x n integer matrix grid consisting of distinct integers from 0 to m * n - 1. You can move in this matrix from a cell to any other cell in the next row. That is, if you are in cell (x, y) such that x < m - 1, you can move to any of the cells (x + 1, 0), (x + 1, 1), …, (x + 1, n - 1). Note that it is not possible to move from cells in the last row.
Each possible move has a cost given by a 0-indexed 2D array moveCost of size (m * n) x n, where moveCost[i][j] is the cost of moving from a cell with value i to a cell in column j of the next row. The cost of moving from cells in the last row of grid can be ignored.
The cost of a path in grid is the sum of all values of cells visited plus the sum of costs of all the moves made. Return the **minimum cost of a path that starts from any cell in the first row and ends at any cell in the last row.**
Example 1:
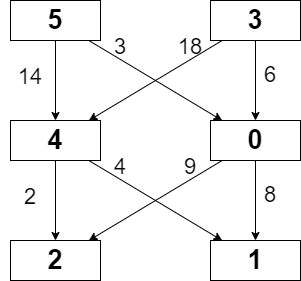
Input: grid = [[5,3],[4,0],[2,1]], moveCost = [[9,8],[1,5],[10,12],[18,6],[2,4],[14,3]]
Output: 17
Explanation: The path with the minimum possible cost is the path 5 -> 0 -> 1.
- The sum of the values of cells visited is 5 + 0 + 1 = 6.
- The cost of moving from 5 to 0 is 3.
- The cost of moving from 0 to 1 is 8.
So the total cost of the path is 6 + 3 + 8 = 17.
Example 2:
Input: grid = [[5,1,2],[4,0,3]], moveCost = [[12,10,15],[20,23,8],[21,7,1],[8,1,13],[9,10,25],[5,3,2]]
Output: 6
Explanation: The path with the minimum possible cost is the path 2 -> 3.
- The sum of the values of cells visited is 2 + 3 = 5.
- The cost of moving from 2 to 3 is 1.
So the total cost of this path is 5 + 1 = 6.
Constraints:
-
m == grid.length -
n == grid[i].length -
2 <= m, n <= 50 -
gridconsists of distinct integers from0tom * n - 1. -
moveCost.length == m * n -
moveCost[i].length == n -
1 <= moveCost[i][j] <= 100
Solution (Java, C++, Python)
-
class Solution { public int minPathCost(int[][] grid, int[][] moveCost) { int m = grid.length; int n = grid[0].length; int[][] dp = new int[m][n]; System.arraycopy(grid[m - 1], 0, dp[m - 1], 0, n); for (int i = m - 2; i >= 0; i--) { for (int j = 0; j < n; j++) { int min = Integer.MAX_VALUE; for (int k = 0; k < n; k++) { min = Math.min(min, grid[i][j] + moveCost[grid[i][j]][k] + dp[i + 1][k]); } dp[i][j] = min; } } int min = Integer.MAX_VALUE; for (int s : dp[0]) { min = Math.min(min, s); } return min; } } ############ class Solution { public int minPathCost(int[][] grid, int[][] moveCost) { int m = grid.length, n = grid[0].length; int[] f = grid[0]; final int inf = 1 << 30; for (int i = 1; i < m; ++i) { int[] g = new int[n]; Arrays.fill(g, inf); for (int j = 0; j < n; ++j) { for (int k = 0; k < n; ++k) { g[j] = Math.min(g[j], f[k] + moveCost[grid[i - 1][k]][j] + grid[i][j]); } } f = g; } // return Arrays.stream(f).min().getAsInt(); int ans = inf; for (int v : f) { ans = Math.min(ans, v); } return ans; } } -
class Solution: def minPathCost(self, grid: List[List[int]], moveCost: List[List[int]]) -> int: m, n = len(grid), len(grid[0]) f = grid[0] for i in range(1, m): g = [inf] * n for j in range(n): for k in range(n): g[j] = min(g[j], f[k] + moveCost[grid[i - 1][k]][j] + grid[i][j]) f = g return min(f) ############ # 2304. Minimum Path Cost in a Grid # https://leetcode.com/problems/minimum-path-cost-in-a-grid/ class Solution: def minPathCost(self, grid: List[List[int]], moveCost: List[List[int]]) -> int: rows, cols = len(grid), len(grid[0]) path = [] res = float('inf') @cache def go(i, j): if i == rows - 1: return grid[i][j] res = float('inf') for k, cost in enumerate(moveCost[grid[i][j]]): res = min(res, go(i + 1, k) + cost + grid[i][j]) return res for j in range(cols): res = min(res, go(0, j)) return res -
class Solution { public: int minPathCost(vector<vector<int>>& grid, vector<vector<int>>& moveCost) { int m = grid.size(), n = grid[0].size(); const int inf = 1 << 30; vector<int> f = grid[0]; for (int i = 1; i < m; ++i) { vector<int> g(n, inf); for (int j = 0; j < n; ++j) { for (int k = 0; k < n; ++k) { g[j] = min(g[j], f[k] + moveCost[grid[i - 1][k]][j] + grid[i][j]); } } f = move(g); } return *min_element(f.begin(), f.end()); } }; -
func minPathCost(grid [][]int, moveCost [][]int) int { m, n := len(grid), len(grid[0]) const inf = 1 << 30 f := grid[0] for i := 1; i < m; i++ { g := make([]int, n) for j := 0; j < n; j++ { g[j] = inf for k := 0; k < n; k++ { g[j] = min(g[j], f[k]+moveCost[grid[i-1][k]][j]+grid[i][j]) } } f = g } ans := inf for _, v := range f { ans = min(ans, v) } return ans } func min(a, b int) int { if a < b { return a } return b } -
function minPathCost(grid: number[][], moveCost: number[][]): number { const m = grid.length, n = grid[0].length; let pre = grid[0].slice(); for (let i = 1; i < m; i++) { let next = new Array(n); for (let j = 0; j < n; j++) { const key = grid[i - 1][j]; for (let k = 0; k < n; k++) { let sum = pre[j] + moveCost[key][k] + grid[i][k]; if (j == 0 || next[k] > sum) { next[k] = sum; } } } pre = next; } return Math.min(...pre); } -
impl Solution { pub fn min_path_cost(grid: Vec<Vec<i32>>, move_cost: Vec<Vec<i32>>) -> i32 { let (m, n) = (grid.len(), grid[0].len()); let mut dp = vec![0; n]; for i in 0..m - 1 { let mut counter = vec![i32::MAX; n]; for j in 0..n { let val = grid[i][j]; for k in 0..n { counter[k] = counter[k].min(val + move_cost[val as usize][k] + dp[j]); } } for j in 0..n { dp[j] = counter[j]; } } let mut res = i32::MAX; for i in 0..n { res = res.min(dp[i] + grid[m - 1][i]); } res } }
Explain:
nope.
Complexity:
- Time complexity : O(n).
- Space complexity : O(n).