Welcome to Subscribe On Youtube
Formatted question description: https://leetcode.ca/all/2218.html
2218. Maximum Value of K Coins From Piles (Hard)
There are n piles of coins on a table. Each pile consists of a positive number of coins of assorted denominations.
In one move, you can choose any coin on top of any pile, remove it, and add it to your wallet.
Given a list piles, where piles[i] is a list of integers denoting the composition of the ith pile from top to bottom, and a positive integer k, return the maximum total value of coins you can have in your wallet if you choose exactly k coins optimally.
Example 1:
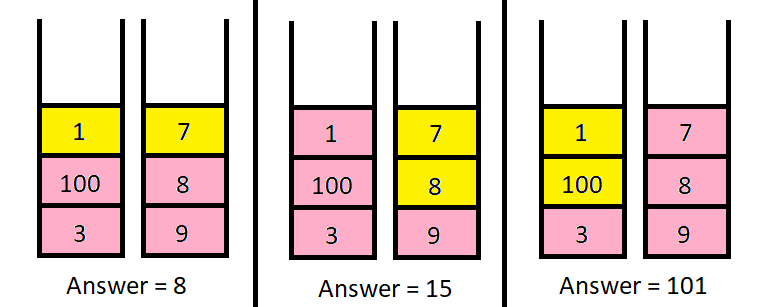
Input: piles = [[1,100,3],[7,8,9]], k = 2 Output: 101 Explanation: The above diagram shows the different ways we can choose k coins. The maximum total we can obtain is 101.
Example 2:
Input: piles = [[100],[100],[100],[100],[100],[100],[1,1,1,1,1,1,700]], k = 7 Output: 706 Explanation: The maximum total can be obtained if we choose all coins from the last pile.
Constraints:
n == piles.length1 <= n <= 10001 <= piles[i][j] <= 1051 <= k <= sum(piles[i].length) <= 2000
Companies:
Google
Related Topics:
Array, Dynamic Programming, Prefix Sum
Similar Questions:
Solution 1. Top-down DP
Let dp[i][j] be the max value of j coins using piles i ~ N-1. The answer is dp[0][k].
For dp[i][j], we can try using t elements from A[i] (0 <= t <= min(j, A[i].size())), getting A[i][0] + ... + A[i][t-1] value plus dp[i+1][j-t] value (the max value of j-t coins using piles i+1 ~ N-1). We try different ts and assign the max value to dp[i][j].
dp[i][j] = max( dp[i+1][j-t] + sum(i, t) | 0 <= t <= min(j, A[i].size()) )
where sum(i, t) = A[i][0] + ... + A[i][t-1]
The trivial case is dp[N][j] = 0, i.e. we can’t get any value from the nonexistent A[N].
-
// OJ: https://leetcode.com/problems/maximum-value-of-k-coins-from-piles/ // Time: O(NM) where `M = sum(A[i].size())` // Space: O(NK) class Solution { public: int maxValueOfCoins(vector<vector<int>>& A, int k) { int N = A.size(), m[1001][2001] = {}; memset(m, -1, sizeof(m)); function<int(int, int)> dp =[&](int i, int j) { if (i == N) return 0; if (m[i][j] != -1) return m[i][j]; int ans = dp(i + 1, j), sum = 0; for (int t = 1; t <= j && t <= A[i].size(); ++t) { sum += A[i][t - 1]; ans = max(ans, dp(i + 1, j - t) + sum); } return m[i][j] = ans; }; return dp(0, k); } }; -
class Solution: def maxValueOfCoins(self, piles: List[List[int]], k: int) -> int: presum = [list(accumulate(p, initial=0)) for p in piles] dp = [0] * (k + 1) for s in presum: for j in range(k, -1, -1): for idx, v in enumerate(s): if j >= idx: dp[j] = max(dp[j], dp[j - idx] + v) return dp[-1] ############ # 2218. Maximum Value of K Coins From Piles # https://leetcode.com/problems/maximum-value-of-k-coins-from-piles/ class Solution: def maxValueOfCoins(self, piles: List[List[int]], K: int) -> int: rows, cols = len(piles), len(piles[0]) @cache def go(rowIndex, k): if k == 0: return 0 if rowIndex == rows: return 0 res = 0 curr = 0 currK = k # skip to take this res = max(res, go(rowIndex + 1, k)) for i, x in enumerate(piles[rowIndex]): curr += x currK -= 1 if currK >= 0: res = max(res, curr + go(rowIndex + 1, currK)) else: break return res return go(0, K) -
class Solution { public int maxValueOfCoins(List<List<Integer>> piles, int k) { int n = piles.size(); List<int[]> presum = new ArrayList<>(); for (List<Integer> p : piles) { int m = p.size(); int[] s = new int[m + 1]; for (int i = 0; i < m; ++i) { s[i + 1] = s[i] + p.get(i); } presum.add(s); } int[] dp = new int[k + 1]; for (int[] s : presum) { for (int j = k; j >= 0; --j) { for (int idx = 0; idx < s.length; ++idx) { if (j >= idx) { dp[j] = Math.max(dp[j], dp[j - idx] + s[idx]); } } } } return dp[k]; } } -
func maxValueOfCoins(piles [][]int, k int) int { var presum [][]int for _, p := range piles { m := len(p) s := make([]int, m+1) for i, v := range p { s[i+1] = s[i] + v } presum = append(presum, s) } dp := make([]int, k+1) for _, s := range presum { for j := k; j >= 0; j-- { for idx, v := range s { if j >= idx { dp[j] = max(dp[j], dp[j-idx]+v) } } } } return dp[k] } func max(a, b int) int { if a > b { return a } return b }
Solution 2. Bottom-up DP
-
// OJ: https://leetcode.com/problems/maximum-value-of-k-coins-from-piles/ // Time: O(NK) // Space: O(NK) class Solution { public: int maxValueOfCoins(vector<vector<int>>& A, int k) { int dp[1001][2001] = {}, N = A.size(); for (int i = 0; i < N; ++i) { for (int j = 1; j <= k; ++j) { dp[i + 1][j] = dp[i][j]; for (int t = 1, sum = 0; t <= j && t <= A[i].size(); ++t) { sum += A[i][t - 1]; dp[i + 1][j] = max(dp[i + 1][j], dp[i][j - t] + sum); } } } return dp[N][k]; } }; -
class Solution: def maxValueOfCoins(self, piles: List[List[int]], k: int) -> int: presum = [list(accumulate(p, initial=0)) for p in piles] dp = [0] * (k + 1) for s in presum: for j in range(k, -1, -1): for idx, v in enumerate(s): if j >= idx: dp[j] = max(dp[j], dp[j - idx] + v) return dp[-1] ############ # 2218. Maximum Value of K Coins From Piles # https://leetcode.com/problems/maximum-value-of-k-coins-from-piles/ class Solution: def maxValueOfCoins(self, piles: List[List[int]], K: int) -> int: rows, cols = len(piles), len(piles[0]) @cache def go(rowIndex, k): if k == 0: return 0 if rowIndex == rows: return 0 res = 0 curr = 0 currK = k # skip to take this res = max(res, go(rowIndex + 1, k)) for i, x in enumerate(piles[rowIndex]): curr += x currK -= 1 if currK >= 0: res = max(res, curr + go(rowIndex + 1, currK)) else: break return res return go(0, K) -
class Solution { public int maxValueOfCoins(List<List<Integer>> piles, int k) { int n = piles.size(); List<int[]> presum = new ArrayList<>(); for (List<Integer> p : piles) { int m = p.size(); int[] s = new int[m + 1]; for (int i = 0; i < m; ++i) { s[i + 1] = s[i] + p.get(i); } presum.add(s); } int[] dp = new int[k + 1]; for (int[] s : presum) { for (int j = k; j >= 0; --j) { for (int idx = 0; idx < s.length; ++idx) { if (j >= idx) { dp[j] = Math.max(dp[j], dp[j - idx] + s[idx]); } } } } return dp[k]; } } -
func maxValueOfCoins(piles [][]int, k int) int { var presum [][]int for _, p := range piles { m := len(p) s := make([]int, m+1) for i, v := range p { s[i+1] = s[i] + v } presum = append(presum, s) } dp := make([]int, k+1) for _, s := range presum { for j := k; j >= 0; j-- { for idx, v := range s { if j >= idx { dp[j] = max(dp[j], dp[j-idx]+v) } } } } return dp[k] } func max(a, b int) int { if a > b { return a } return b }
The space complexity can be reduced to O(K).
-
// OJ: https://leetcode.com/problems/maximum-value-of-k-coins-from-piles/ // Time: O(NK) // Space: O(K) class Solution { public: int maxValueOfCoins(vector<vector<int>>& A, int k) { int dp[2001] = {}, N = A.size(); for (int i = 0; i < N; ++i) { for (int j = k; j >= 1; --j) { for (int t = 1, sum = 0; t <= j && t <= A[i].size(); ++t) { sum += A[i][t - 1]; dp[j] = max(dp[j], dp[j - t] + sum); } } } return dp[k]; } }; -
class Solution: def maxValueOfCoins(self, piles: List[List[int]], k: int) -> int: presum = [list(accumulate(p, initial=0)) for p in piles] dp = [0] * (k + 1) for s in presum: for j in range(k, -1, -1): for idx, v in enumerate(s): if j >= idx: dp[j] = max(dp[j], dp[j - idx] + v) return dp[-1] ############ # 2218. Maximum Value of K Coins From Piles # https://leetcode.com/problems/maximum-value-of-k-coins-from-piles/ class Solution: def maxValueOfCoins(self, piles: List[List[int]], K: int) -> int: rows, cols = len(piles), len(piles[0]) @cache def go(rowIndex, k): if k == 0: return 0 if rowIndex == rows: return 0 res = 0 curr = 0 currK = k # skip to take this res = max(res, go(rowIndex + 1, k)) for i, x in enumerate(piles[rowIndex]): curr += x currK -= 1 if currK >= 0: res = max(res, curr + go(rowIndex + 1, currK)) else: break return res return go(0, K) -
class Solution { public int maxValueOfCoins(List<List<Integer>> piles, int k) { int n = piles.size(); List<int[]> presum = new ArrayList<>(); for (List<Integer> p : piles) { int m = p.size(); int[] s = new int[m + 1]; for (int i = 0; i < m; ++i) { s[i + 1] = s[i] + p.get(i); } presum.add(s); } int[] dp = new int[k + 1]; for (int[] s : presum) { for (int j = k; j >= 0; --j) { for (int idx = 0; idx < s.length; ++idx) { if (j >= idx) { dp[j] = Math.max(dp[j], dp[j - idx] + s[idx]); } } } } return dp[k]; } } -
func maxValueOfCoins(piles [][]int, k int) int { var presum [][]int for _, p := range piles { m := len(p) s := make([]int, m+1) for i, v := range p { s[i+1] = s[i] + v } presum = append(presum, s) } dp := make([]int, k+1) for _, s := range presum { for j := k; j >= 0; j-- { for idx, v := range s { if j >= idx { dp[j] = max(dp[j], dp[j-idx]+v) } } } } return dp[k] } func max(a, b int) int { if a > b { return a } return b }
Discuss
https://leetcode.com/problems/maximum-value-of-k-coins-from-piles/discuss/1886910