Welcome to Subscribe On Youtube
Formatted question description: https://leetcode.ca/all/2204.html
2204. Distance to a Cycle in Undirected Graph
Description
You are given a positive integer n representing the number of nodes in a connected undirected graph containing exactly one cycle. The nodes are numbered from 0 to n - 1 (inclusive).
You are also given a 2D integer array edges, where edges[i] = [node1i, node2i] denotes that there is a bidirectional edge connecting node1i and node2i in the graph.
The distance between two nodes a and b is defined to be the minimum number of edges that are needed to go from a to b.
Return an integer array answer of size n, where answer[i] is the minimum distance between the ith node and any node in the cycle.
Example 1:
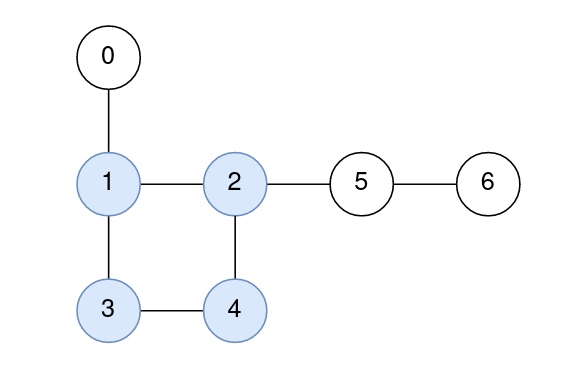
Input: n = 7, edges = [[1,2],[2,4],[4,3],[3,1],[0,1],[5,2],[6,5]] Output: [1,0,0,0,0,1,2] Explanation: The nodes 1, 2, 3, and 4 form the cycle. The distance from 0 to 1 is 1. The distance from 1 to 1 is 0. The distance from 2 to 2 is 0. The distance from 3 to 3 is 0. The distance from 4 to 4 is 0. The distance from 5 to 2 is 1. The distance from 6 to 2 is 2.
Example 2:
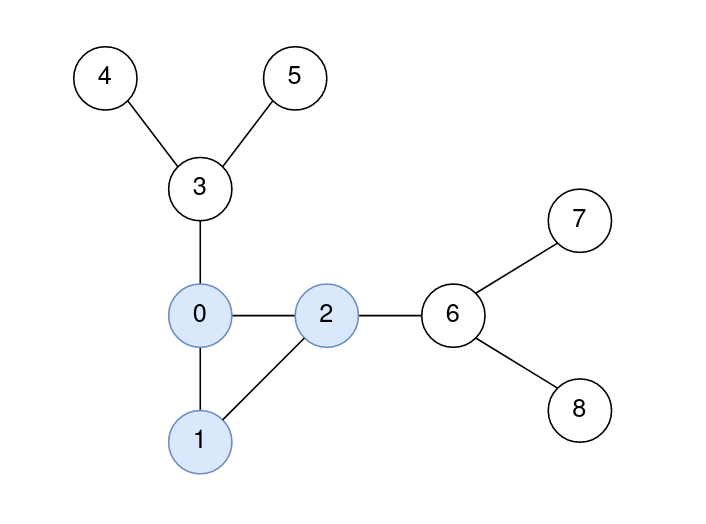
Input: n = 9, edges = [[0,1],[1,2],[0,2],[2,6],[6,7],[6,8],[0,3],[3,4],[3,5]] Output: [0,0,0,1,2,2,1,2,2] Explanation: The nodes 0, 1, and 2 form the cycle. The distance from 0 to 0 is 0. The distance from 1 to 1 is 0. The distance from 2 to 2 is 0. The distance from 3 to 1 is 1. The distance from 4 to 1 is 2. The distance from 5 to 1 is 2. The distance from 6 to 2 is 1. The distance from 7 to 2 is 2. The distance from 8 to 2 is 2.
Constraints:
3 <= n <= 105edges.length == nedges[i].length == 20 <= node1i, node2i <= n - 1node1i != node2i- The graph is connected.
- The graph has exactly one cycle.
- There is at most one edge between any pair of vertices.
Solutions
Solution 1: Topological Sorting
We can first convert the edges in $edges$ into an adjacency list $g$, where $g[i]$ represents all adjacent nodes of node $i$, represented as a set.
Next, we delete nodes layer by layer from the outside to the inside until only a cycle remains. The specific method is as follows:
We first find all nodes with a degree of $1$ and remove these nodes from the graph. If after deletion, the degree of its adjacent node becomes $1$, then we add it to the queue $q$. During this process, we record all deleted nodes in order as $seq$; and we use an array $f$ to record the adjacent node of each node that is closer to the cycle, i.e., $f[i]$ represents the adjacent node of node $i$ that is closer to the cycle.
Finally, we initialize an answer array $ans$ of length $n$, where $ans[i]$ represents the minimum distance from node $i$ to any node in the cycle, initially $ans[i] = 0$. Then, we start traversing from the end of $seq$. For each node $i$, we can get the value of $ans[i]$ from its adjacent node $f[i]$, i.e., $ans[i] = ans[f[i]] + 1$.
After the traversal, return the answer array $ans$.
The time complexity is $O(n)$, and the space complexity is $O(n)$. Here, $n$ is the number of nodes.
Similar problems:
-
class Solution { public int[] distanceToCycle(int n, int[][] edges) { Set<Integer>[] g = new Set[n]; Arrays.setAll(g, k -> new HashSet<>()); for (var e : edges) { int a = e[0], b = e[1]; g[a].add(b); g[b].add(a); } Deque<Integer> q = new ArrayDeque<>(); for (int i = 0; i < n; ++i) { if (g[i].size() == 1) { q.offer(i); } } int[] f = new int[n]; Deque<Integer> seq = new ArrayDeque<>(); while (!q.isEmpty()) { int i = q.poll(); seq.push(i); for (int j : g[i]) { g[j].remove(i); f[i] = j; if (g[j].size() == 1) { q.offer(j); } } } int[] ans = new int[n]; while (!seq.isEmpty()) { int i = seq.pop(); ans[i] = ans[f[i]] + 1; } return ans; } } -
class Solution { public: vector<int> distanceToCycle(int n, vector<vector<int>>& edges) { unordered_set<int> g[n]; for (auto& e : edges) { int a = e[0], b = e[1]; g[a].insert(b); g[b].insert(a); } queue<int> q; for (int i = 0; i < n; ++i) { if (g[i].size() == 1) { q.push(i); } } int f[n]; int seq[n]; int k = 0; while (!q.empty()) { int i = q.front(); q.pop(); seq[k++] = i; for (int j : g[i]) { g[j].erase(i); f[i] = j; if (g[j].size() == 1) { q.push(j); } } g[i].clear(); } vector<int> ans(n); for (; k; --k) { int i = seq[k - 1]; ans[i] = ans[f[i]] + 1; } return ans; } }; -
class Solution: def distanceToCycle(self, n: int, edges: List[List[int]]) -> List[int]: g = defaultdict(set) for a, b in edges: g[a].add(b) g[b].add(a) q = deque(i for i in range(n) if len(g[i]) == 1) f = [0] * n seq = [] while q: i = q.popleft() seq.append(i) for j in g[i]: g[j].remove(i) f[i] = j if len(g[j]) == 1: q.append(j) g[i].clear() ans = [0] * n for i in seq[::-1]: ans[i] = ans[f[i]] + 1 return ans -
func distanceToCycle(n int, edges [][]int) []int { g := make([]map[int]bool, n) for i := range g { g[i] = map[int]bool{} } for _, e := range edges { a, b := e[0], e[1] g[a][b] = true g[b][a] = true } q := []int{} for i := 0; i < n; i++ { if len(g[i]) == 1 { q = append(q, i) } } f := make([]int, n) seq := []int{} for len(q) > 0 { i := q[0] q = q[1:] seq = append(seq, i) for j := range g[i] { delete(g[j], i) f[i] = j if len(g[j]) == 1 { q = append(q, j) } } g[i] = map[int]bool{} } ans := make([]int, n) for k := len(seq) - 1; k >= 0; k-- { i := seq[k] ans[i] = ans[f[i]] + 1 } return ans } -
function distanceToCycle(n: number, edges: number[][]): number[] { const g: Set<number>[] = new Array(n).fill(0).map(() => new Set<number>()); for (const [a, b] of edges) { g[a].add(b); g[b].add(a); } const q: number[] = []; for (let i = 0; i < n; ++i) { if (g[i].size === 1) { q.push(i); } } const f: number[] = Array(n).fill(0); const seq: number[] = []; while (q.length) { const i = q.pop()!; seq.push(i); for (const j of g[i]) { g[j].delete(i); f[i] = j; if (g[j].size === 1) { q.push(j); } } g[i].clear(); } const ans: number[] = Array(n).fill(0); while (seq.length) { const i = seq.pop()!; ans[i] = ans[f[i]] + 1; } return ans; }