Formatted question description: https://leetcode.ca/all/2203.html

2203. Minimum Weighted Subgraph With the Required Paths (Hard)

You are given an integer n denoting the number of nodes of a weighted directed graph. The nodes are numbered from 0 to n - 1.

You are also given a 2D integer array edges where edges[i] = [from_i, to_i, weight_i] denotes that there exists a directed edge from from_i to to_i with weight weight_i.

Lastly, you are given three distinct integers src1, src2, and dest denoting three distinct nodes of the graph.

Return the minimum weight of a subgraph of the graph such that it is possible to reach dest from both src1 and src2 via a set of edges of this subgraph. In case such a subgraph does not exist, return -1.

A subgraph is a graph whose vertices and edges are subsets of the original graph. The weight of a subgraph is the sum of weights of its constituent edges.

Example 1:

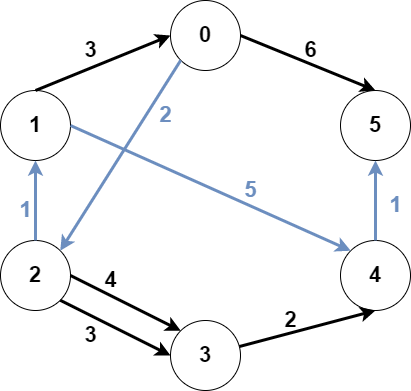
Input: n = 6, edges = [[0,2,2],[0,5,6],[1,0,3],[1,4,5],[2,1,1],[2,3,3],[2,3,4],[3,4,2],[4,5,1]], src1 = 0, src2 = 1, dest = 5
Output: 9
Explanation:
The above figure represents the input graph.
The blue edges represent one of the subgraphs that yield the optimal answer.
Note that the subgraph [[1,0,3],[0,5,6]] also yields the optimal answer. It is not possible to get a subgraph with less weight satisfying all the constraints.

Example 2:

Input: n = 3, edges = [[0,1,1],[2,1,1]], src1 = 0, src2 = 1, dest = 2
Output: -1
Explanation:
The above figure represents the input graph.
It can be seen that there does not exist any path from node 1 to node 2, hence there are no subgraphs satisfying all the constraints.

Constraints:

3 <= n <= 10⁵
0 <= edges.length <= 10⁵
edges[i].length == 3
0 <= from_i, to_i, src1, src2, dest <= n - 1
from_i != to_i
src1, src2, and dest are pairwise distinct.
1 <= weight[i] <= 10⁵

Related Topics:
Graph, Shortest Path

Similar Questions:

Minimum Cost to Make at Least One Valid Path in a Grid (Hard)
Solution 1. Dijkstra

Do Dijkstra 3 times.

First time: store the shortest distance from node a to all other nodes in array da.

Second time: store the shortest distance from node b to all other nodes in array db.

Third time: store the shortest distance from node dest to all other nodes via Reversed Graph in array dd.

The answer is the minimum da[i] + db[i] + dd[i] (0 <= i < N).

Intuition

// OJ: https://leetcode.com/problems/minimum-weighted-subgraph-with-the-required-paths/
// Time: O(ElogE + N)
// Space: O(E)
class Solution {
    typedef pair<long, long> ipair;
public:
    long long minimumWeight(int n, vector<vector<int>>& E, int a, int b, int dest) {
        vector<vector<ipair>> G(n), R(n); // `G` is the original graph. `R` is the reversed graph
        for (auto &e : E) {
            int u = e[0], v = e[1], w = e[2];
            G[u].emplace_back(v, w);
            R[v].emplace_back(u, w);
        }
        vector<long> da(n, LONG_MAX), db(n, LONG_MAX), dd(n, LONG_MAX);
        auto dijkstra = [&](vector<vector<ipair>> &G, int src, vector<long> &dist) {
            priority_queue<ipair, vector<ipair>, greater<>> pq;
            pq.emplace(0, src);
            dist[src] = 0;
            while (pq.size()) {
                auto [cost, u] = pq.top();
                pq.pop();
                if (cost > dist[u]) continue;
                for (auto &[v, w] : G[u]) {
                    if (dist[v] > dist[u] + w) {
                        dist[v] = dist[u] + w;
                        pq.emplace(dist[v], v);
                    }
                }
            }
        };
        dijkstra(G, a, da);
        dijkstra(G, b, db);
        dijkstra(R, dest, dd);
        long ans = LONG_MAX;
        for (int i = 0; i < n; ++i) {
            if (da[i] == LONG_MAX || db[i] == LONG_MAX || dd[i] == LONG_MAX) continue;
            ans = min(ans, da[i] + db[i] + dd[i]);
        }
        return ans == LONG_MAX ? -1 : ans;
    }
};

class Solution:
    def minimumWeight(
        self, n: int, edges: List[List[int]], src1: int, src2: int, dest: int
    ) -> int:
        def dijkstra(g, u):
            dist = [inf] * n
            dist[u] = 0
            q = [(0, u)]
            while q:
                d, u = heappop(q)
                if d > dist[u]:
                    continue
                for v, w in g[u]:
                    if dist[v] > dist[u] + w:
                        dist[v] = dist[u] + w
                        heappush(q, (dist[v], v))
            return dist

        g = defaultdict(list)
        rg = defaultdict(list)
        for f, t, w in edges:
            g[f].append((t, w))
            rg[t].append((f, w))
        d1 = dijkstra(g, src1)
        d2 = dijkstra(g, src2)
        d3 = dijkstra(rg, dest)
        ans = min(sum(v) for v in zip(d1, d2, d3))
        return -1 if ans >= inf else ans

############

# 2203. Minimum Weighted Subgraph With the Required Paths
# https://leetcode.com/problems/minimum-weighted-subgraph-with-the-required-paths/

class Solution:
    def minimumWeight(self, n: int, edges: List[List[int]], src1: int, src2: int, dest: int) -> int:
        G = defaultdict(list)
        RG = defaultdict(list)
        
        for x, y, w in edges:
            G[x].append((y, w))
            RG[y].append((x, w))
        
        def dijkstra(graph, src):
            dist = [float('inf')] * n
            dist[src] = 0
            pq = [(0, src)]
            
            while pq:
                d, node = heapq.heappop(pq)
                
                if dist[node] != d: continue
                
                for nei, w in graph[node]:
                    old = dist[nei]
                    new = d + w
                    
                    if new < old:
                        dist[nei] = new
                        heapq.heappush(pq, (new, nei))
            
            return dist
        
        A = dijkstra(G, src1)
        B = dijkstra(G, src2)
        C = dijkstra(RG, dest)
        
        res = float('inf')
        
        for a, b, c in zip(A, B, C):
            res = min(res, a + b + c)
        
        return -1 if res == float('inf') else res
            
            

class Solution {
    private static final Long INF = Long.MAX_VALUE;

    public long minimumWeight(int n, int[][] edges, int src1, int src2, int dest) {
        List<Pair<Integer, Long>>[] g = new List[n];
        List<Pair<Integer, Long>>[] rg = new List[n];
        for (int i = 0; i < n; ++i) {
            g[i] = new ArrayList<>();
            rg[i] = new ArrayList<>();
        }
        for (int[] e : edges) {
            int f = e[0], t = e[1];
            long w = e[2];
            g[f].add(new Pair<>(t, w));
            rg[t].add(new Pair<>(f, w));
        }
        long[] d1 = dijkstra(g, src1);
        long[] d2 = dijkstra(g, src2);
        long[] d3 = dijkstra(rg, dest);
        long ans = -1;
        for (int i = 0; i < n; ++i) {
            if (d1[i] == INF || d2[i] == INF || d3[i] == INF) {
                continue;
            }
            long t = d1[i] + d2[i] + d3[i];
            if (ans == -1 || ans > t) {
                ans = t;
            }
        }
        return ans;
    }

    private long[] dijkstra(List<Pair<Integer, Long>>[] g, int u) {
        int n = g.length;
        long[] dist = new long[n];
        Arrays.fill(dist, INF);
        dist[u] = 0;
        PriorityQueue<Pair<Long, Integer>> q
            = new PriorityQueue<>(Comparator.comparingLong(Pair::getKey));
        q.offer(new Pair<>(0L, u));
        while (!q.isEmpty()) {
            Pair<Long, Integer> p = q.poll();
            long d = p.getKey();
            u = p.getValue();
            if (d > dist[u]) {
                continue;
            }
            for (Pair<Integer, Long> e : g[u]) {
                int v = e.getKey();
                long w = e.getValue();
                if (dist[v] > dist[u] + w) {
                    dist[v] = dist[u] + w;
                    q.offer(new Pair<>(dist[v], v));
                }
            }
        }
        return dist;
    }
}

Discuss

https://leetcode.com/problems/minimum-weighted-subgraph-with-the-required-paths/discuss/1844091/

Link to illustration: https://whimsical.com/2203-GLgvvsWiXznXswwd5YrmzM

2203 - Minimum Weighted Subgraph With the Required Paths

2203. Minimum Weighted Subgraph With the Required Paths (Hard)

Solution 1. Dijkstra

Discuss

All Problems

All Solutions

Welcome to Subscribe On Youtube

2203. Minimum Weighted Subgraph With the Required Paths (Hard)

Solution 1. Dijkstra

Discuss

All Problems

All Solutions