Welcome to Subscribe On Youtube
2271. Maximum White Tiles Covered by a Carpet
Description
You are given a 2D integer array tiles where tiles[i] = [li, ri] represents that every tile j in the range li <= j <= ri is colored white.
You are also given an integer carpetLen, the length of a single carpet that can be placed anywhere.
Return the maximum number of white tiles that can be covered by the carpet.
Example 1:
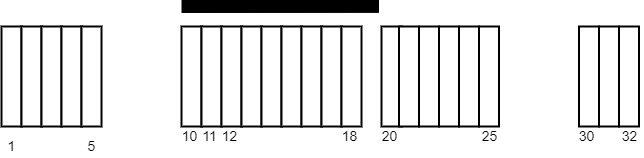
Input: tiles = [[1,5],[10,11],[12,18],[20,25],[30,32]], carpetLen = 10 Output: 9 Explanation: Place the carpet starting on tile 10. It covers 9 white tiles, so we return 9. Note that there may be other places where the carpet covers 9 white tiles. It can be shown that the carpet cannot cover more than 9 white tiles.
Example 2:
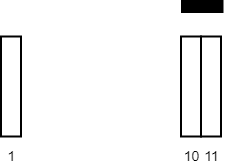
Input: tiles = [[10,11],[1,1]], carpetLen = 2 Output: 2 Explanation: Place the carpet starting on tile 10. It covers 2 white tiles, so we return 2.
Constraints:
1 <= tiles.length <= 5 * 104tiles[i].length == 21 <= li <= ri <= 1091 <= carpetLen <= 109- The
tilesare non-overlapping.
Solutions
-
class Solution { public int maximumWhiteTiles(int[][] tiles, int carpetLen) { Arrays.sort(tiles, (a, b) -> a[0] - b[0]); int n = tiles.length; int s = 0, ans = 0; for (int i = 0, j = 0; i < n; ++i) { while (j < n && tiles[j][1] - tiles[i][0] + 1 <= carpetLen) { s += tiles[j][1] - tiles[j][0] + 1; ++j; } if (j < n && tiles[i][0] + carpetLen > tiles[j][0]) { ans = Math.max(ans, s + tiles[i][0] + carpetLen - tiles[j][0]); } else { ans = Math.max(ans, s); } s -= (tiles[i][1] - tiles[i][0] + 1); } return ans; } } -
class Solution { public: int maximumWhiteTiles(vector<vector<int>>& tiles, int carpetLen) { sort(tiles.begin(), tiles.end()); int s = 0, ans = 0, n = tiles.size(); for (int i = 0, j = 0; i < n; ++i) { while (j < n && tiles[j][1] - tiles[i][0] + 1 <= carpetLen) { s += tiles[j][1] - tiles[j][0] + 1; ++j; } if (j < n && tiles[i][0] + carpetLen > tiles[j][0]) { ans = max(ans, s + tiles[i][0] + carpetLen - tiles[j][0]); } else { ans = max(ans, s); } s -= (tiles[i][1] - tiles[i][0] + 1); } return ans; } }; -
class Solution: def maximumWhiteTiles(self, tiles: List[List[int]], carpetLen: int) -> int: tiles.sort() n = len(tiles) s = ans = j = 0 for i, (li, ri) in enumerate(tiles): while j < n and tiles[j][1] - li + 1 <= carpetLen: s += tiles[j][1] - tiles[j][0] + 1 j += 1 if j < n and li + carpetLen > tiles[j][0]: ans = max(ans, s + li + carpetLen - tiles[j][0]) else: ans = max(ans, s) s -= ri - li + 1 return ans -
func maximumWhiteTiles(tiles [][]int, carpetLen int) int { sort.Slice(tiles, func(i, j int) bool { return tiles[i][0] < tiles[j][0] }) n := len(tiles) s, ans := 0, 0 for i, j := 0, 0; i < n; i++ { for j < n && tiles[j][1]-tiles[i][0]+1 <= carpetLen { s += tiles[j][1] - tiles[j][0] + 1 j++ } if j < n && tiles[i][0]+carpetLen > tiles[j][0] { ans = max(ans, s+tiles[i][0]+carpetLen-tiles[j][0]) } else { ans = max(ans, s) } s -= (tiles[i][1] - tiles[i][0] + 1) } return ans }