Welcome to Subscribe On Youtube
2201. Count Artifacts That Can Be Extracted
Description
There is an n x n 0-indexed grid with some artifacts buried in it. You are given the integer n and a 0-indexed 2D integer array artifacts describing the positions of the rectangular artifacts where artifacts[i] = [r1i, c1i, r2i, c2i] denotes that the ith artifact is buried in the subgrid where:
(r1i, c1i)is the coordinate of the top-left cell of theithartifact and(r2i, c2i)is the coordinate of the bottom-right cell of theithartifact.
You will excavate some cells of the grid and remove all the mud from them. If the cell has a part of an artifact buried underneath, it will be uncovered. If all the parts of an artifact are uncovered, you can extract it.
Given a 0-indexed 2D integer array dig where dig[i] = [ri, ci] indicates that you will excavate the cell (ri, ci), return the number of artifacts that you can extract.
The test cases are generated such that:
- No two artifacts overlap.
- Each artifact only covers at most
4cells. - The entries of
digare unique.
Example 1:
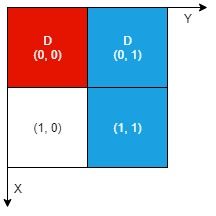
Input: n = 2, artifacts = [[0,0,0,0],[0,1,1,1]], dig = [[0,0],[0,1]] Output: 1 Explanation: The different colors represent different artifacts. Excavated cells are labeled with a 'D' in the grid. There is 1 artifact that can be extracted, namely the red artifact. The blue artifact has one part in cell (1,1) which remains uncovered, so we cannot extract it. Thus, we return 1.
Example 2:
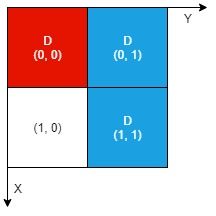
Input: n = 2, artifacts = [[0,0,0,0],[0,1,1,1]], dig = [[0,0],[0,1],[1,1]] Output: 2 Explanation: Both the red and blue artifacts have all parts uncovered (labeled with a 'D') and can be extracted, so we return 2.
Constraints:
1 <= n <= 10001 <= artifacts.length, dig.length <= min(n2, 105)artifacts[i].length == 4dig[i].length == 20 <= r1i, c1i, r2i, c2i, ri, ci <= n - 1r1i <= r2ic1i <= c2i- No two artifacts will overlap.
- The number of cells covered by an artifact is at most
4. - The entries of
digare unique.
Solutions
Solution 1: Hash Table
We can use a hash table $s$ to record all the excavated cells, then traverse all the workpieces, and check whether all parts of the workpiece are in the hash table. If so, we can extract the workpiece, and the answer is increased by one.
The time complexity is $O(m + k)$, and the space complexity is $O(k)$. Here, $m$ is the number of workpieces, and $k$ is the number of excavated cells.
-
class Solution { private Set<Integer> s = new HashSet<>(); private int n; public int digArtifacts(int n, int[][] artifacts, int[][] dig) { this.n = n; for (var p : dig) { s.add(p[0] * n + p[1]); } int ans = 0; for (var a : artifacts) { ans += check(a); } return ans; } private int check(int[] a) { int x1 = a[0], y1 = a[1], x2 = a[2], y2 = a[3]; for (int x = x1; x <= x2; ++x) { for (int y = y1; y <= y2; ++y) { if (!s.contains(x * n + y)) { return 0; } } } return 1; } } -
class Solution { public: int digArtifacts(int n, vector<vector<int>>& artifacts, vector<vector<int>>& dig) { unordered_set<int> s; for (auto& p : dig) { s.insert(p[0] * n + p[1]); } auto check = [&](vector<int>& a) { int x1 = a[0], y1 = a[1], x2 = a[2], y2 = a[3]; for (int x = x1; x <= x2; ++x) { for (int y = y1; y <= y2; ++y) { if (!s.count(x * n + y)) { return 0; } } } return 1; }; int ans = 0; for (auto& a : artifacts) { ans += check(a); } return ans; } }; -
class Solution: def digArtifacts( self, n: int, artifacts: List[List[int]], dig: List[List[int]] ) -> int: def check(a: List[int]) -> bool: x1, y1, x2, y2 = a return all( (x, y) in s for x in range(x1, x2 + 1) for y in range(y1, y2 + 1) ) s = {(i, j) for i, j in dig} return sum(check(a) for a in artifacts) -
func digArtifacts(n int, artifacts [][]int, dig [][]int) (ans int) { s := map[int]bool{} for _, p := range dig { s[p[0]*n+p[1]] = true } check := func(a []int) int { x1, y1, x2, y2 := a[0], a[1], a[2], a[3] for x := x1; x <= x2; x++ { for y := y1; y <= y2; y++ { if !s[x*n+y] { return 0 } } } return 1 } for _, a := range artifacts { ans += check(a) } return } -
function digArtifacts(n: number, artifacts: number[][], dig: number[][]): number { const s: Set<number> = new Set(); for (const [x, y] of dig) { s.add(x * n + y); } let ans = 0; const check = (a: number[]): number => { const [x1, y1, x2, y2] = a; for (let x = x1; x <= x2; ++x) { for (let y = y1; y <= y2; ++y) { if (!s.has(x * n + y)) { return 0; } } } return 1; }; for (const a of artifacts) { ans += check(a); } return ans; } -
use std::collections::HashSet; impl Solution { pub fn dig_artifacts(n: i32, artifacts: Vec<Vec<i32>>, dig: Vec<Vec<i32>>) -> i32 { let mut s: HashSet<i32> = HashSet::new(); for p in dig { s.insert(p[0] * n + p[1]); } let check = |a: &[i32]| -> i32 { let x1 = a[0]; let y1 = a[1]; let x2 = a[2]; let y2 = a[3]; for x in x1..=x2 { for y in y1..=y2 { if !s.contains(&(x * n + y)) { return 0; } } } 1 }; let mut ans = 0; for a in artifacts { ans += check(&a); } ans } }