Welcome to Subscribe On Youtube
2132. Stamping the Grid
Description
You are given an m x n binary matrix grid where each cell is either 0 (empty) or 1 (occupied).
You are then given stamps of size stampHeight x stampWidth. We want to fit the stamps such that they follow the given restrictions and requirements:
- Cover all the empty cells.
- Do not cover any of the occupied cells.
- We can put as many stamps as we want.
- Stamps can overlap with each other.
- Stamps are not allowed to be rotated.
- Stamps must stay completely inside the grid.
Return true if it is possible to fit the stamps while following the given restrictions and requirements. Otherwise, return false.
Example 1:
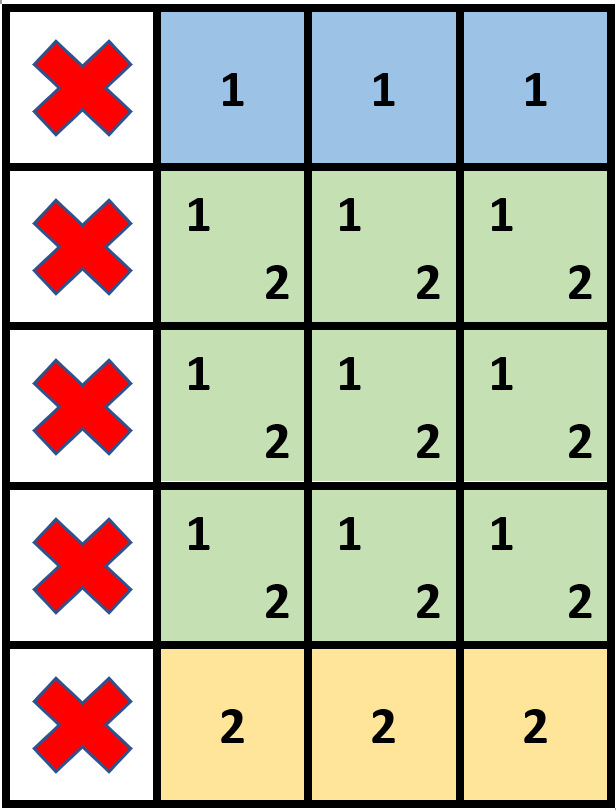
Input: grid = [[1,0,0,0],[1,0,0,0],[1,0,0,0],[1,0,0,0],[1,0,0,0]], stampHeight = 4, stampWidth = 3 Output: true Explanation: We have two overlapping stamps (labeled 1 and 2 in the image) that are able to cover all the empty cells.
Example 2:
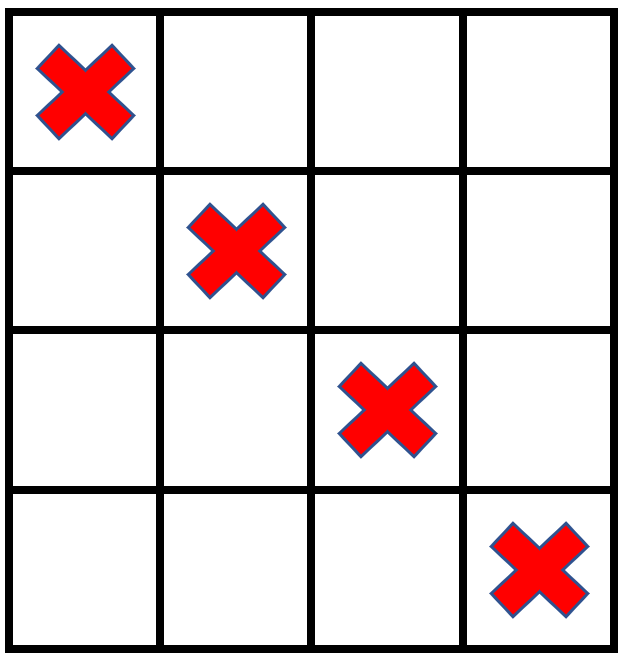
Input: grid = [[1,0,0,0],[0,1,0,0],[0,0,1,0],[0,0,0,1]], stampHeight = 2, stampWidth = 2 Output: false Explanation: There is no way to fit the stamps onto all the empty cells without the stamps going outside the grid.
Constraints:
m == grid.lengthn == grid[r].length1 <= m, n <= 1051 <= m * n <= 2 * 105grid[r][c]is either0or1.1 <= stampHeight, stampWidth <= 105
Solutions
Solution 1: Two-Dimensional Prefix Sum + Two-Dimensional Difference
According to the problem description, every empty cell must be covered by a stamp, and no occupied cell can be covered. Therefore, we can traverse the two-dimensional matrix, and for each cell, if all cells in the area of $stampHeight \times stampWidth$ with this cell as the upper left corner are empty (i.e., not occupied), then we can place a stamp at this cell.
To quickly determine whether all cells in an area are empty, we can use a two-dimensional prefix sum. We use $s_{i,j}$ to represent the number of occupied cells in the sub-matrix from $(1,1)$ to $(i,j)$ in the two-dimensional matrix. That is, $s_{i, j} = s_{i - 1, j} + s_{i, j - 1} - s_{i - 1, j - 1} + grid_{i-1, j-1}$.
Then, with $(i, j)$ as the upper left corner, and the height and width are $stampHeight$ and $stampWidth$ respectively, the lower right coordinate of the sub-matrix is $(x, y) = (i + stampHeight - 1, j + stampWidth - 1)$. We can calculate the number of occupied cells in this sub-matrix through $s_{x, y} - s_{x, j - 1} - s_{i - 1, y} + s_{i - 1, j - 1}$. If the number of occupied cells in this sub-matrix is $0$, then we can place a stamp at $(i, j)$. After placing the stamp, all cells in this $stampHeight \times stampWidth$ area will become occupied cells. We can use a two-dimensional difference array $d$ to record this change. That is:
\[\begin{aligned} d_{i, j} &\leftarrow d_{i, j} + 1 \\ d_{i, y + 1} &\leftarrow d_{i, y + 1} - 1 \\ d_{x + 1, j} &\leftarrow d_{x + 1, j} - 1 \\ d_{x + 1, y + 1} &\leftarrow d_{x + 1, y + 1} + 1 \end{aligned}\]Finally, we perform a prefix sum operation on the two-dimensional difference array $d$ to find out the number of times each cell is covered by a stamp. If a cell is not occupied and the number of times it is covered by a stamp is $0$, then we cannot place a stamp at this cell, so we need to return $\texttt{false}$. If all “unoccupied cells” are successfully covered by stamps, return $\texttt{true}$.
The time complexity is $O(m \times n)$, and the space complexity is $O(m \times n)$. Here, $m$ and $n$ are the height and width of the two-dimensional matrix, respectively.
-
class Solution { public boolean possibleToStamp(int[][] grid, int stampHeight, int stampWidth) { int m = grid.length, n = grid[0].length; int[][] s = new int[m + 1][n + 1]; for (int i = 1; i <= m; ++i) { for (int j = 1; j <= n; ++j) { s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + grid[i - 1][j - 1]; } } int[][] d = new int[m + 2][n + 2]; for (int i = 1; i + stampHeight - 1 <= m; ++i) { for (int j = 1; j + stampWidth - 1 <= n; ++j) { int x = i + stampHeight - 1, y = j + stampWidth - 1; if (s[x][y] - s[x][j - 1] - s[i - 1][y] + s[i - 1][j - 1] == 0) { d[i][j]++; d[i][y + 1]--; d[x + 1][j]--; d[x + 1][y + 1]++; } } } for (int i = 1; i <= m; ++i) { for (int j = 1; j <= n; ++j) { d[i][j] += d[i - 1][j] + d[i][j - 1] - d[i - 1][j - 1]; if (grid[i - 1][j - 1] == 0 && d[i][j] == 0) { return false; } } } return true; } } -
class Solution { public: bool possibleToStamp(vector<vector<int>>& grid, int stampHeight, int stampWidth) { int m = grid.size(), n = grid[0].size(); vector<vector<int>> s(m + 1, vector<int>(n + 1)); for (int i = 1; i <= m; ++i) { for (int j = 1; j <= n; ++j) { s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + grid[i - 1][j - 1]; } } vector<vector<int>> d(m + 2, vector<int>(n + 2)); for (int i = 1; i + stampHeight - 1 <= m; ++i) { for (int j = 1; j + stampWidth - 1 <= n; ++j) { int x = i + stampHeight - 1, y = j + stampWidth - 1; if (s[x][y] - s[x][j - 1] - s[i - 1][y] + s[i - 1][j - 1] == 0) { d[i][j]++; d[i][y + 1]--; d[x + 1][j]--; d[x + 1][y + 1]++; } } } for (int i = 1; i <= m; ++i) { for (int j = 1; j <= n; ++j) { d[i][j] += d[i - 1][j] + d[i][j - 1] - d[i - 1][j - 1]; if (grid[i - 1][j - 1] == 0 && d[i][j] == 0) { return false; } } } return true; } }; -
class Solution: def possibleToStamp( self, grid: List[List[int]], stampHeight: int, stampWidth: int ) -> bool: m, n = len(grid), len(grid[0]) s = [[0] * (n + 1) for _ in range(m + 1)] for i, row in enumerate(grid, 1): for j, v in enumerate(row, 1): s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + v d = [[0] * (n + 2) for _ in range(m + 2)] for i in range(1, m - stampHeight + 2): for j in range(1, n - stampWidth + 2): x, y = i + stampHeight - 1, j + stampWidth - 1 if s[x][y] - s[x][j - 1] - s[i - 1][y] + s[i - 1][j - 1] == 0: d[i][j] += 1 d[i][y + 1] -= 1 d[x + 1][j] -= 1 d[x + 1][y + 1] += 1 for i, row in enumerate(grid, 1): for j, v in enumerate(row, 1): d[i][j] += d[i - 1][j] + d[i][j - 1] - d[i - 1][j - 1] if v == 0 and d[i][j] == 0: return False return True -
func possibleToStamp(grid [][]int, stampHeight int, stampWidth int) bool { m, n := len(grid), len(grid[0]) s := make([][]int, m+1) for i := range s { s[i] = make([]int, n+1) } for i := 1; i <= m; i++ { for j := 1; j <= n; j++ { s[i][j] = s[i-1][j] + s[i][j-1] - s[i-1][j-1] + grid[i-1][j-1] } } d := make([][]int, m+2) for i := range d { d[i] = make([]int, n+2) } for i := 1; i+stampHeight-1 <= m; i++ { for j := 1; j+stampWidth-1 <= n; j++ { x, y := i+stampHeight-1, j+stampWidth-1 if s[x][y]-s[x][j-1]-s[i-1][y]+s[i-1][j-1] == 0 { d[i][j]++ d[i][y+1]-- d[x+1][j]-- d[x+1][y+1]++ } } } for i := 1; i <= m; i++ { for j := 1; j <= n; j++ { d[i][j] += d[i-1][j] + d[i][j-1] - d[i-1][j-1] if grid[i-1][j-1] == 0 && d[i][j] == 0 { return false } } } return true } -
function possibleToStamp(grid: number[][], stampHeight: number, stampWidth: number): boolean { const m = grid.length; const n = grid[0].length; const s: number[][] = Array.from({ length: m + 1 }, () => Array(n + 1).fill(0)); for (let i = 1; i <= m; ++i) { for (let j = 1; j <= n; ++j) { s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + grid[i - 1][j - 1]; } } const d: number[][] = Array.from({ length: m + 2 }, () => Array(n + 2).fill(0)); for (let i = 1; i + stampHeight - 1 <= m; ++i) { for (let j = 1; j + stampWidth - 1 <= n; ++j) { const [x, y] = [i + stampHeight - 1, j + stampWidth - 1]; if (s[x][y] - s[x][j - 1] - s[i - 1][y] + s[i - 1][j - 1] === 0) { d[i][j]++; d[i][y + 1]--; d[x + 1][j]--; d[x + 1][y + 1]++; } } } for (let i = 1; i <= m; ++i) { for (let j = 1; j <= n; ++j) { d[i][j] += d[i - 1][j] + d[i][j - 1] - d[i - 1][j - 1]; if (grid[i - 1][j - 1] === 0 && d[i][j] === 0) { return false; } } } return true; } -
/** * @param {number[][]} grid * @param {number} stampHeight * @param {number} stampWidth * @return {boolean} */ var possibleToStamp = function (grid, stampHeight, stampWidth) { const m = grid.length; const n = grid[0].length; const s = Array.from({ length: m + 1 }, () => Array(n + 1).fill(0)); for (let i = 1; i <= m; ++i) { for (let j = 1; j <= n; ++j) { s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + grid[i - 1][j - 1]; } } const d = Array.from({ length: m + 2 }, () => Array(n + 2).fill(0)); for (let i = 1; i + stampHeight - 1 <= m; ++i) { for (let j = 1; j + stampWidth - 1 <= n; ++j) { const [x, y] = [i + stampHeight - 1, j + stampWidth - 1]; if (s[x][y] - s[x][j - 1] - s[i - 1][y] + s[i - 1][j - 1] === 0) { d[i][j]++; d[i][y + 1]--; d[x + 1][j]--; d[x + 1][y + 1]++; } } } for (let i = 1; i <= m; ++i) { for (let j = 1; j <= n; ++j) { d[i][j] += d[i - 1][j] + d[i][j - 1] - d[i - 1][j - 1]; if (grid[i - 1][j - 1] === 0 && d[i][j] === 0) { return false; } } } return true; }; -
impl Solution { pub fn possible_to_stamp(grid: Vec<Vec<i32>>, stamp_height: i32, stamp_width: i32) -> bool { let n: usize = grid.len(); let m: usize = grid[0].len(); let mut prefix_vec: Vec<Vec<i32>> = vec![vec![0; m + 1]; n + 1]; // Initialize the prefix vector for i in 0..n { for j in 0..m { prefix_vec[i + 1][j + 1] = prefix_vec[i][j + 1] + prefix_vec[i + 1][j] - prefix_vec[i][j] + grid[i][j]; } } let mut diff_vec: Vec<Vec<i32>> = vec![vec![0; m + 1]; n + 1]; // Construct the difference vector based on prefix sum vector for i in 0..n { for j in 0..m { // If the value of the cell is one, just bypass this if grid[i][j] == 1 { continue; } // Otherwise, try stick the stamp let x: usize = i + (stamp_height as usize); let y: usize = j + (stamp_width as usize); // Check the bound if x <= n && y <= m { // If the region can be sticked (All cells are empty, which means the sum will be zero) if prefix_vec[x][y] - prefix_vec[x][j] - prefix_vec[i][y] + prefix_vec[i][j] == 0 { // Update the difference vector diff_vec[i][j] += 1; diff_vec[x][y] += 1; diff_vec[x][j] -= 1; diff_vec[i][y] -= 1; } } } } let mut check_vec: Vec<Vec<i32>> = vec![vec![0; m + 1]; n + 1]; // Check the prefix sum of difference vector, to determine if there is any empty cell left for i in 0..n { for j in 0..m { // If the value of the cell is one, just bypass this if grid[i][j] == 1 { continue; } // Otherwise, check if the region is empty, by calculating the prefix sum of difference vector check_vec[i + 1][j + 1] = check_vec[i][j + 1] + check_vec[i + 1][j] - check_vec[i][j] + diff_vec[i][j]; if check_vec[i + 1][j + 1] == 0 { return false; } } } true } }