Welcome to Subscribe On Youtube
1976. Number of Ways to Arrive at Destination
Formatted question description: https://leetcode.ca/all/1976.html
Level
Medium
Description
You are in a city that consists of n intersections numbered from 0 to n - 1 with bi-directional roads between some intersections. The inputs are generated such that you can reach any intersection from any other intersection and that there is at most one road between any two intersections.
You are given an integer n and a 2D integer array roads where roads[i] = [u_i, v_i, time_i] means that there is a road between intersections u_i and v_i that takes time_i minutes to travel. You want to know in how many ways you can travel from intersection 0 to intersection n - 1 in the shortest amount of time.
Return the number of ways you can arrive at your destination in the shortest amount of time. Since the answer may be large, return it modulo 10^9 + 7.
Example 1:
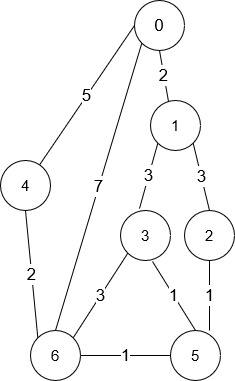
Input: n = 7, roads = [[0,6,7],[0,1,2],[1,2,3],[1,3,3],[6,3,3],[3,5,1],[6,5,1],[2,5,1],[0,4,5],[4,6,2]]
Output: 4
Explanation: The shortest amount of time it takes to go from intersection 0 to intersection 6 is 7 minutes.
The four ways to get there in 7 minutes are:
- 0 ➝ 6
- 0 ➝ 4 ➝ 6
- 0 ➝ 1 ➝ 2 ➝ 5 ➝ 6
- 0 ➝ 1 ➝ 3 ➝ 5 ➝ 6
Example 2:
Input: n = 2, roads = [[1,0,10]]
Output: 1
Explanation: There is only one way to go from intersection 0 to intersection 1, and it takes 10 minutes.
Constraints:
1 <= n <= 200n - 1 <= roads.length <= n * (n - 1) / 2roads[i].length == 30 <= u_i, v_i <= n - 11 <= time_i <= 10^9u_i != v_i- There is at most one road connecting any two intersections.
- You can reach any intersection from any other intersection.
Solution
Calculate the shortest time to arrive at each intersection from intersection 0 using Dijkstra's algorithm. Then starting from intersection 0, calculate the number of ways to arrive at each intersection with the shortest time. Finally, return the number of ways to arrive at intersection n - 1.
-
class Solution { private static final long INF = Long.MAX_VALUE / 2; private static final int MOD = (int) 1e9 + 7; public int countPaths(int n, int[][] roads) { long[][] g = new long[n][n]; long[] dist = new long[n]; long[] w = new long[n]; boolean[] vis = new boolean[n]; for (int i = 0; i < n; ++i) { Arrays.fill(g[i], INF); Arrays.fill(dist, INF); } for (int[] r : roads) { int u = r[0], v = r[1], t = r[2]; g[u][v] = t; g[v][u] = t; } g[0][0] = 0; dist[0] = 0; w[0] = 1; for (int i = 0; i < n; ++i) { int t = -1; for (int j = 0; j < n; ++j) { if (!vis[j] && (t == -1 || dist[j] < dist[t])) { t = j; } } vis[t] = true; for (int j = 0; j < n; ++j) { if (j == t) { continue; } long ne = dist[t] + g[t][j]; if (dist[j] > ne) { dist[j] = ne; w[j] = w[t]; } else if (dist[j] == ne) { w[j] = (w[j] + w[t]) % MOD; } } } return (int) w[n - 1]; } } -
// OJ: https://leetcode.com/problems/number-of-ways-to-arrive-at-destination/ // Time: O(ElogE) // Space: O(V + E) class Solution { typedef pair<long, long> ipair; public: int countPaths(int n, vector<vector<int>>& E) { vector<vector<pair<int, int>>> G(n); for (auto &e : E) { int u = e[0], v = e[1], t = e[2]; G[u].emplace_back(v, t); G[v].emplace_back(u, t); } long mod = 1e9 + 7; vector<long> dist(n, LONG_MAX), cnt(n); priority_queue<ipair, vector<ipair>, greater<>> pq; // time, city dist[0] = 0; cnt[0] = 1; pq.emplace(0, 0); while (pq.size()) { auto [cost, u] = pq.top(); pq.pop(); if (cost > dist[u]) continue; for (auto &[v, time] : G[u]) { long c = cost + time; if (c < dist[v]) { dist[v] = c; cnt[v] = cnt[u]; pq.emplace(c, v); } else if (c == dist[v]) cnt[v] = (cnt[v] + cnt[u]) % mod; } } return cnt[n - 1]; } }; -
# 1976. Number of Ways to Arrive at Destination # https://leetcode.com/problems/number-of-ways-to-arrive-at-destination/ ''' In Python 3, 10**9 + 7 is a commonly used constant in competitive programming and algorithmic contests. It is often used as a modular arithmetic prime number for computing hash values, counting permutations and combinations, and in various other mathematical computations. The reason for using 10**9 + 7 is that it is a large prime number that fits within the 32-bit integer limit. This means that arithmetic operations on this number can be performed efficiently using 32-bit integer arithmetic, which is significantly faster than using 64-bit arithmetic. Furthermore, 10**9 + 7 is a safe prime, which means that it has certain properties that make it useful for cryptographic applications. Specifically, it is a prime of the form 2*p + 1, where p is also a prime. This means that it has a large prime factor, making it difficult to factorize and making it suitable for use in cryptographic algorithms. Overall, the number 10**9 + 7 is a useful constant in Python 3 and is often used in algorithmic programming for its properties as a large prime and a safe prime. ''' class Solution: def countPaths(self, n: int, roads: List[List[int]]) -> int: G = defaultdict(list) for x, y, w in roads: G[x].append((y, w)) G[y].append((x, w)) time_cost = [float('inf')] * n time_cost[0] = 0 path_cnt = [0] * n path_cnt[0] = 1 heap = [(0, 0)] # (min_cost, idx) , default order min->max while heap: (min_cost, idx) = heappop(heap) if idx == n-1: return path_cnt[idx] % (10**9 + 7) # or just break out of this while loop for neib, weight in G[idx]: candidate = min_cost + weight if candidate == time_cost[neib]: # add new paths to counting paths reaching 'neib' path_cnt[neib] += path_cnt[idx] elif candidate < time_cost[neib]: # dist[neib] initialized as float('inf') time_cost[neib] = candidate path_cnt[neib] = path_cnt[idx] heappush(heap, (candidate, neib)) return path_cnt[-1] ############ class Solution: def countPaths(self, n: int, roads: List[List[int]]) -> int: INF = inf MOD = 10**9 + 7 g = [[INF] * n for _ in range(n)] for u, v, t in roads: g[u][v] = t g[v][u] = t g[0][0] = 0 dist = [INF] * n w = [0] * n dist[0] = 0 w[0] = 1 vis = [False] * n for _ in range(n): t = -1 for i in range(n): if not vis[i] and (t == -1 or dist[i] < dist[t]): t = i vis[t] = True for i in range(n): if i == t: continue ne = dist[t] + g[t][i] if dist[i] > ne: dist[i] = ne w[i] = w[t] elif dist[i] == ne: w[i] += w[t] return w[-1] % MOD -
func countPaths(n int, roads [][]int) int { const inf = math.MaxInt64 / 2 const mod = int(1e9) + 7 g := make([][]int, n) dist := make([]int, n) w := make([]int, n) vis := make([]bool, n) for i := range g { g[i] = make([]int, n) dist[i] = inf for j := range g[i] { g[i][j] = inf } } for _, r := range roads { u, v, t := r[0], r[1], r[2] g[u][v], g[v][u] = t, t } g[0][0] = 0 dist[0] = 0 w[0] = 1 for i := 0; i < n; i++ { t := -1 for j := 0; j < n; j++ { if !vis[j] && (t == -1 || dist[t] > dist[j]) { t = j } } vis[t] = true for j := 0; j < n; j++ { if j == t { continue } ne := dist[t] + g[t][j] if dist[j] > ne { dist[j] = ne w[j] = w[t] } else if dist[j] == ne { w[j] = (w[j] + w[t]) % mod } } } return w[n-1] }