Welcome to Subscribe On Youtube

Formatted question description: https://leetcode.ca/all/1975.html

1975. Maximum Matrix Sum

Level

Medium

Description

You are given an n x n integer matrix. You can do the following operation any number of times:

• Choose any two adjacent elements of matrix and multiply each of them by -1.

Two elements are considered adjacent if and only if they share a border.

Your goal is to maximize the summation of the matrix’s elements. Return the maximum sum of the matrix’s elements using the operation mentioned above.

Example 1:

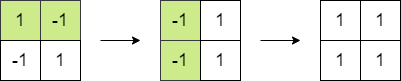
Input: matrix = [[1,-1],[-1,1]]

Output: 4

Explanation: We can follow the following steps to reach sum equals 4:

• Multiply the 2 elements in the first row by -1.
• Multiply the 2 elements in the first column by -1.

Example 2:

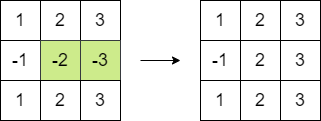
Input: matrix = [[1,2,3],[-1,-2,-3],[1,2,3]]

Output: 16

Explanation: We can follow the following step to reach sum equals 16:

• Multiply the 2 last elements in the second row by -1.

Constraints:

• n == matrix.length == matrix[i].length
• 2 <= n <= 250
• -10^5 <= matrix[i][j] <= 10^5

Solution

To get the maximum matrix sum, at most one element can be negative after performing the operation any number of times. If there is no element 0 and the number of negative elements is odd, then there has to be one negative element. Otherwise, all elements can be non-negative. If there has to be one negative element, it should have the minimum absolute value. Therefore, find the element with the minimum absolute value and make it negative if there has to be one negative element (the element can be positive in the original matrix), and calculate the sum of elements in the matrix.

• Java
• C++
• Python
• Go
• Javascript

• class Solution {
      public long maxMatrixSum(int[][] matrix) {
          long sum = 0;
          int minPositive = Integer.MAX_VALUE;
          int minNegative = Integer.MIN_VALUE;
          int positiveCount = 0, negativeCount = 0, zeroCount = 0;
          int side = matrix.length;
          for (int i = 0; i < side; i++) {
              for (int j = 0; j < side; j++) {
                  int num = matrix[i][j];
                  sum += Math.abs(num);
                  if (num > 0) {
                      minPositive = Math.min(minPositive, num);
                      positiveCount++;
                  } else if (num < 0) {
                      minNegative = Math.max(minNegative, num);
                      negativeCount++;
                  } else
                      zeroCount++;
              }
          }
          if (zeroCount > 0 || negativeCount % 2 == 0)
              return sum;
          if (positiveCount == 0)
              return sum += minNegative * 2;
          int minPositiveAbs = minPositive, minNegativeAbs = -minNegative;
          sum -= Math.min(minPositiveAbs, minNegativeAbs) * 2;
          return sum;
      }
  }
  
  ############
  
  class Solution {
      public long maxMatrixSum(int[][] matrix) {
          long s = 0;
          int cnt = 0;
          int mi = Integer.MAX_VALUE;
          for (var row : matrix) {
              for (var v : row) {
                  s += Math.abs(v);
                  mi = Math.min(mi, Math.abs(v));
                  if (v < 0) {
                      ++cnt;
                  }
              }
          }
          if (cnt % 2 == 0 || mi == 0) {
              return s;
          }
          return s - mi * 2;
      }
  }
  

• // OJ: https://leetcode.com/problems/maximum-matrix-sum/
  // Time: O(N^2)
  // Space: O(1)
  class Solution {
  public:
      long long maxMatrixSum(vector<vector<int>>& A) {
          long long cnt = 0, sum = 0, N = A.size(), mn = INT_MAX;
          for (int i = 0; i < N; ++i) {
              for (int j = 0; j < N; ++j) {
                  cnt += A[i][j] < 0;
                  sum += abs(A[i][j]);
                  mn = min(mn, (long long)abs(A[i][j]));
              }
          }
          return cnt % 2 ? sum - 2 * mn : sum;
      }
  };
  

• class Solution:
      def maxMatrixSum(self, matrix: List[List[int]]) -> int:
          s = cnt = 0
          mi = inf
          for row in matrix:
              for v in row:
                  s += abs(v)
                  mi = min(mi, abs(v))
                  if v < 0:
                      cnt += 1
          if cnt % 2 == 0 or mi == 0:
              return s
          return s - mi * 2
  
  ############
  
  # 1975. Maximum Matrix Sum
  # https://leetcode.com/problems/maximum-matrix-sum/
  
  class Solution:
      def maxMatrixSum(self, matrix: List[List[int]]) -> int:
          rows, cols = len(matrix), len(matrix[0])
          total = count = 0
          mmin = float('inf')
          
          for i in range(rows):
              for j in range(cols):
                  total += abs(matrix[i][j])
                  
                  if matrix[i][j] < 0: count += 1
                  mmin = min(mmin, abs(matrix[i][j]))
          
          if count % 2 == 0:
              return total
          else:
              return total - 2 * mmin
          
          
  
  

• func maxMatrixSum(matrix [][]int) int64 {
  	s := 0
  	cnt, mi := 0, math.MaxInt32
  	for _, row := range matrix {
  		for _, v := range row {
  			s += abs(v)
  			mi = min(mi, abs(v))
  			if v < 0 {
  				cnt++
  			}
  		}
  	}
  	if cnt%2 == 1 {
  		s -= mi * 2
  	}
  	return int64(s)
  }
  
  func min(a, b int) int {
  	if a < b {
  		return a
  	}
  	return b
  }
  
  func abs(x int) int {
  	if x < 0 {
  		return -x
  	}
  	return x
  }
  

• /**
   * @param {number[][]} matrix
   * @return {number}
   */
  var maxMatrixSum = function (matrix) {
      let cnt = 0;
      let s = 0;
      let mi = Infinity;
      for (const row of matrix) {
          for (const v of row) {
              s += Math.abs(v);
              mi = Math.min(mi, Math.abs(v));
              cnt += v < 0;
          }
      }
      if (cnt % 2 == 0) {
          return s;
      }
      return s - mi * 2;
  };
  
  

All Problems

All Solutions