Formatted question description: https://leetcode.ca/all/1970.html

1970. Last Day Where You Can Still Cross

Level

Hard

Description

There is a 1-based binary matrix where 0 represents land and 1 represents water. You are given integers row and col representing the number of rows and columns in the matrix, respectively.

Initially on day 0, the entire matrix is land. However, each day a new cell becomes flooded with water. You are given a 1-based 2D array cells, where cells[i] = [r_i, c_i] represents that on the i-th day, the cell on the r_i-th row and c_i-th column (1-based coordinates) will be covered with water (i.e., changed to 1).

You want to find the last day that it is possible to walk from the top to the bottom by only walking on land cells. You can start from any cell in the top row and end at any cell in the bottom row. You can only travel in the four cardinal directions (left, right, up, and down).

Return the last day where it is possible to walk from the top to the bottom by only walking on land cells.

Example 1:

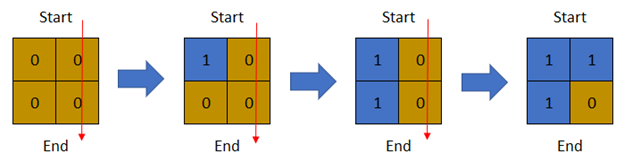
Image text

Input: row = 2, col = 2, cells = [[1,1],[2,1],[1,2],[2,2]]

Output: 2

Explanation: The above image depicts how the matrix changes each day starting from day 0. The last day where it is possible to cross from top to bottom is on day 2.

Example 2:

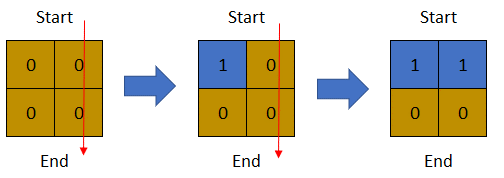
Image text

Input: row = 2, col = 2, cells = [[1,1],[1,2],[2,1],[2,2]]

Output: 1

Explanation: The above image depicts how the matrix changes each day starting from day 0. The last day where it is possible to cross from top to bottom is on day 1.

Example 3:

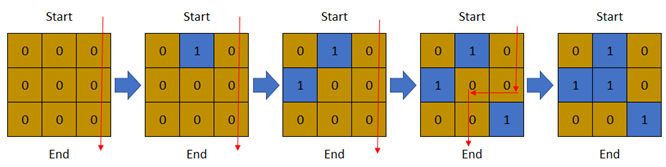
Image text

Input: row = 3, col = 3, cells = [[1,2],[2,1],[3,3],[2,2],[1,1],[1,3],[2,3],[3,2],[3,1]]

Output: 3

Explanation: The above image depicts how the matrix changes each day starting from day 0. The last day where it is possible to cross from top to bottom is on day 3.

Constraints:

2 <= row, col <= 2 * 10^4
4 <= row * col <= 2 * 10^4
cells.length == row * col
1 <= r_i <= row
1 <= c_i <= col
All the values of cells are unique.

Solution

The maximum possible value of last day is row * col - 1 and the minimum possible value of last day is col - 1. Use binary search to find the last day. Each time let mid be the mean of high and low, apply the first mid elements in cells as water cells, and check whether it is possible to walk from top to bottom.

class Solution {
    static final int WATER = -1;
    static final int WHITE = 0;
    static final int BLACK = 1;
    int[][] directions = { {-1, 0}, {1, 0}, {0, -1}, {0, 1} };

    public int latestDayToCross(int row, int col, int[][] cells) {
        int low = col - 1, high = row * col - 1;
        while (low < high) {
            int mid = (high - low + 1) / 2 + low;
            boolean canCross = check(row, col, cells, mid);
            if (canCross)
                low = mid;
            else
                high = mid - 1;
        }
        return low;
    }

    public boolean check(int row, int col, int[][] cells, int mid) {
        int[][] grid = new int[row][col];
        for (int i = 0; i < mid; i++) {
            int[] cell = cells[i];
            grid[cell[0] - 1][cell[1] - 1] = WATER;
        }
        Queue<int[]> queue = new LinkedList<int[]>();
        for (int j = 0; j < col; j++) {
            if (grid[0][j] == WHITE) {
                grid[0][j] = BLACK;
                queue.offer(new int[]{0, j});
            }
        }
        while (!queue.isEmpty()) {
            int[] cell = queue.poll();
            int r = cell[0], c = cell[1];
            for (int[] direction : directions) {
                int newR = r + direction[0], newC = c + direction[1];
                if (newR >= 0 && newR < row && newC >= 0 && newC < col && grid[newR][newC] == WHITE) {
                    if (newR == row - 1)
                        return true;
                    grid[newR][newC] = BLACK;
                    queue.offer(new int[]{newR, newC});
                }
            }
        }
        return false;
    }
}

############

class Solution {
    private int[] p;
    private int row;
    private int col;
    private boolean[][] grid;
    private int[][] dirs = new int[][] { {0, -1}, {0, 1}, {1, 0}, {-1, 0}};

    public int latestDayToCross(int row, int col, int[][] cells) {
        int n = row * col;
        this.row = row;
        this.col = col;
        p = new int[n + 2];
        for (int i = 0; i < p.length; ++i) {
            p[i] = i;
        }
        grid = new boolean[row][col];
        int top = n, bottom = n + 1;
        for (int k = cells.length - 1; k >= 0; --k) {
            int i = cells[k][0] - 1, j = cells[k][1] - 1;
            grid[i][j] = true;
            for (int[] e : dirs) {
                if (check(i + e[0], j + e[1])) {
                    p[find(i * col + j)] = find((i + e[0]) * col + j + e[1]);
                }
            }
            if (i == 0) {
                p[find(i * col + j)] = find(top);
            }
            if (i == row - 1) {
                p[find(i * col + j)] = find(bottom);
            }
            if (find(top) == find(bottom)) {
                return k;
            }
        }
        return 0;
    }

    private int find(int x) {
        if (p[x] != x) {
            p[x] = find(p[x]);
        }
        return p[x];
    }

    private boolean check(int i, int j) {
        return i >= 0 && i < row && j >= 0 && j < col && grid[i][j];
    }
}

class Solution:
    def latestDayToCross(self, row: int, col: int, cells: List[List[int]]) -> int:
        n = row * col
        p = list(range(n + 2))
        grid = [[False] * col for _ in range(row)]
        top, bottom = n, n + 1

        def find(x):
            if p[x] != x:
                p[x] = find(p[x])
            return p[x]

        def check(i, j):
            return 0 <= i < row and 0 <= j < col and grid[i][j]

        for k in range(len(cells) - 1, -1, -1):
            i, j = cells[k][0] - 1, cells[k][1] - 1
            grid[i][j] = True
            for x, y in [[0, 1], [0, -1], [1, 0], [-1, 0]]:
                if check(i + x, j + y):
                    p[find(i * col + j)] = find((i + x) * col + j + y)
            if i == 0:
                p[find(i * col + j)] = find(top)
            if i == row - 1:
                p[find(i * col + j)] = find(bottom)
            if find(top) == find(bottom):
                return k
        return 0

############

# 1970. Last Day Where You Can Still Cross
# https://leetcode.com/problems/last-day-where-you-can-still-cross/

class Solution:
    def latestDayToCross(self, rows: int, cols: int, cells: List[List[int]]) -> int:

        def good(days):
            lands = [[0] * cols for _ in range(rows)]
            
            for i in range(days):
                x, y = cells[i]
                lands[x - 1][y - 1] = 1
            
            queue = collections.deque()
            for y in range(cols):
                if lands[0][y] == 0:
                    queue.append((0, y))
                    lands[0][y] = 1
            
            while queue:
                x, y = queue.popleft()
                if x == rows - 1: return True

                for dx, dy in ((x + 1, y), (x - 1, y), (x, y + 1), (x, y - 1)):
                    if 0 <= dx < rows and 0 <= dy < cols and lands[dx][dy] == 0:
                        queue.append((dx, dy))
                        lands[dx][dy] = 1
            
            return False
        
        left, right = 1, len(cells)
        res = 0
        
        while left <= right:
            mid = left + (right - left) // 2
            
            if good(mid):
                res = mid
                left = mid + 1
            else:
                right = mid - 1
                
        return res
            

class Solution {
public:
    vector<int> p;
    int dirs[4][2] = { {0, -1}, {0, 1}, {1, 0}, {-1, 0} };
    int row, col;

    int latestDayToCross(int row, int col, vector<vector<int>>& cells) {
        int n = row * col;
        this->row = row;
        this->col = col;
        p.resize(n + 2);
        for (int i = 0; i < p.size(); ++i) p[i] = i;
        vector<vector<bool>> grid(row, vector<bool>(col, false));
        int top = n, bottom = n + 1;
        for (int k = cells.size() - 1; k >= 0; --k) {
            int i = cells[k][0] - 1, j = cells[k][1] - 1;
            grid[i][j] = true;
            for (auto e : dirs) {
                if (check(i + e[0], j + e[1], grid)) {
                    p[find(i * col + j)] = find((i + e[0]) * col + j + e[1]);
                }
            }
            if (i == 0) p[find(i * col + j)] = find(top);
            if (i == row - 1) p[find(i * col + j)] = find(bottom);
            if (find(top) == find(bottom)) return k;
        }
        return 0;
    }

    bool check(int i, int j, vector<vector<bool>>& grid) {
        return i >= 0 && i < row && j >= 0 && j < col && grid[i][j];
    }

    int find(int x) {
        if (p[x] != x) p[x] = find(p[x]);
        return p[x];
    }
};

var p []int

func latestDayToCross(row int, col int, cells [][]int) int {
	n := row * col
	p = make([]int, n+2)
	for i := 0; i < len(p); i++ {
		p[i] = i
	}
	grid := make([][]bool, row)
	for i := 0; i < row; i++ {
		grid[i] = make([]bool, col)
	}
	top, bottom := n, n+1
	dirs := [4][2]int{ {0, -1}, {0, 1}, {1, 0}, {-1, 0} }
	for k := len(cells) - 1; k >= 0; k-- {
		i, j := cells[k][0]-1, cells[k][1]-1
		grid[i][j] = true
		for _, e := range dirs {
			if check(i+e[0], j+e[1], grid) {
				p[find(i*col+j)] = find((i+e[0])*col + j + e[1])
			}
		}
		if i == 0 {
			p[find(i*col+j)] = find(top)
		}
		if i == row-1 {
			p[find(i*col+j)] = find(bottom)
		}
		if find(top) == find(bottom) {
			return k
		}
	}
	return 0
}

func check(i, j int, grid [][]bool) bool {
	return i >= 0 && i < len(grid) && j >= 0 && j < len(grid[0]) && grid[i][j]
}

func find(x int) int {
	if p[x] != x {
		p[x] = find(p[x])
	}
	return p[x]
}

1970 - Last Day Where You Can Still Cross

1970. Last Day Where You Can Still Cross

Level

Description

Solution

All Problems

All Solutions

Welcome to Subscribe On Youtube

1970. Last Day Where You Can Still Cross

Level

Description

Solution

All Problems

All Solutions