Welcome to Subscribe On Youtube

2054. Two Best Non-Overlapping Events

Description

You are given a 0-indexed 2D integer array of events where events[i] = [startTimei, endTimei, valuei]. The ith event starts at startTimei and ends at endTimei, and if you attend this event, you will receive a value of valuei. You can choose at most two non-overlapping events to attend such that the sum of their values is maximized.

Return this maximum sum.

Note that the start time and end time is inclusive: that is, you cannot attend two events where one of them starts and the other ends at the same time. More specifically, if you attend an event with end time t, the next event must start at or after t + 1.

 

Example 1:

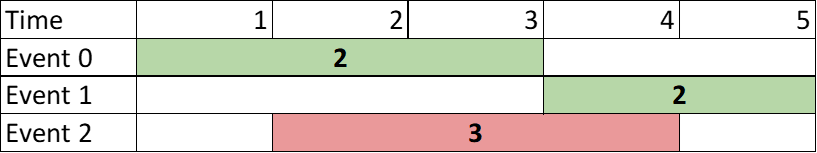
Input: events = [[1,3,2],[4,5,2],[2,4,3]]
Output: 4
Explanation: Choose the green events, 0 and 1 for a sum of 2 + 2 = 4.

Example 2:

Input: events = [[1,3,2],[4,5,2],[1,5,5]]
Output: 5
Explanation: Choose event 2 for a sum of 5.

Example 3:

Input: events = [[1,5,3],[1,5,1],[6,6,5]]
Output: 8
Explanation: Choose events 0 and 2 for a sum of 3 + 5 = 8.

 

Constraints:

• 2 <= events.length <= 105
• events[i].length == 3
• 1 <= startTimei <= endTimei <= 109
• 1 <= valuei <= 106

Solutions

• Java
• C++
• Python
• Go

• class Solution {
      public int maxTwoEvents(int[][] events) {
          Arrays.sort(events, (a, b) -> a[0] - b[0]);
          int n = events.length;
          int[] f = new int[n + 1];
          for (int i = n - 1; i >= 0; --i) {
              f[i] = Math.max(f[i + 1], events[i][2]);
          }
          int ans = 0;
          for (int[] e : events) {
              int v = e[2];
              int left = 0, right = n;
              while (left < right) {
                  int mid = (left + right) >> 1;
                  if (events[mid][0] > e[1]) {
                      right = mid;
                  } else {
                      left = mid + 1;
                  }
              }
              if (left < n) {
                  v += f[left];
              }
              ans = Math.max(ans, v);
          }
          return ans;
      }
  }
  

• class Solution {
  public:
      int maxTwoEvents(vector<vector<int>>& events) {
          sort(events.begin(), events.end());
          int n = events.size();
          vector<int> f(n + 1);
          for (int i = n - 1; ~i; --i) f[i] = max(f[i + 1], events[i][2]);
          int ans = 0;
          for (auto& e : events) {
              int v = e[2];
              int left = 0, right = n;
              while (left < right) {
                  int mid = (left + right) >> 1;
                  if (events[mid][0] > e[1])
                      right = mid;
                  else
                      left = mid + 1;
              }
              if (left < n) v += f[left];
              ans = max(ans, v);
          }
          return ans;
      }
  };
  

• class Solution:
      def maxTwoEvents(self, events: List[List[int]]) -> int:
          events.sort()
          n = len(events)
          f = [events[-1][2]] * n
          for i in range(n - 2, -1, -1):
              f[i] = max(f[i + 1], events[i][2])
          ans = 0
          for _, e, v in events:
              idx = bisect_right(events, e, key=lambda x: x[0])
              if idx < n:
                  v += f[idx]
              ans = max(ans, v)
          return ans
  
  

• func maxTwoEvents(events [][]int) int {
  	sort.Slice(events, func(i, j int) bool {
  		return events[i][0] < events[j][0]
  	})
  	n := len(events)
  	f := make([]int, n+1)
  	for i := n - 1; i >= 0; i-- {
  		f[i] = max(f[i+1], events[i][2])
  	}
  	ans := 0
  	for _, e := range events {
  		v := e[2]
  		left, right := 0, n
  		for left < right {
  			mid := (left + right) >> 1
  			if events[mid][0] > e[1] {
  				right = mid
  			} else {
  				left = mid + 1
  			}
  		}
  		if left < n {
  			v += f[left]
  		}
  		ans = max(ans, v)
  	}
  	return ans
  }
  

All Problems

All Solutions