Welcome to Subscribe On Youtube
Formatted question description: https://leetcode.ca/all/1761.html
1761. Minimum Degree of a Connected Trio in a Graph
Level
Hard
Description
You are given an undirected graph. You are given an integer n which is the number of nodes in the graph and an array edges, where each edges[i] = [u_i, v_i] indicates that there is an undirected edge between u_i and v_i.
A connected trio is a set of three nodes where there is an edge between every pair of them.
The degree of a connected trio is the number of edges where one endpoint is in the trio, and the other is not.
Return the minimum degree of a connected trio in the graph, or -1 if the graph has no connected trios.
Example 1:
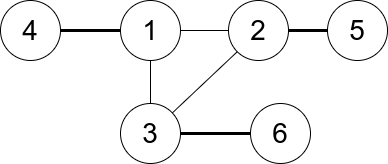
Input: n = 6, edges = [[1,2],[1,3],[3,2],[4,1],[5,2],[3,6]]
Output: 3
Explanation: There is exactly one trio, which is [1,2,3]. The edges that form its degree are bolded in the figure above.
Example 2:
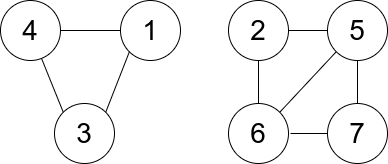
Input: n = 7, edges = [[1,3],[4,1],[4,3],[2,5],[5,6],[6,7],[7,5],[2,6]]
Output: 0
Explanation: There are exactly three trios:
1) [1,4,3] with degree 0.
2) [2,5,6] with degree 2.
3) [5,6,7] with degree 2.
Constraints:
2 <= n <= 400edges[i].length == 21 <= edges.length <= n * (n-1) / 21 <= u_i, v_i <= nu_i != v_i- There are no repeated edges.
Solution
Use a hash map to store each node’s connected nodes. Then loop over all tuples of nodes and determine whether the three nodes form a connected trio. If the three nodes form a connected trio, calculate the sum of the numbers of edges that connect to the three nodes and subtract 6 from the sum (to exclude the edges inside the trio). During the process, maintain the minimum degree. Finally, return the minimum degree.
-
class Solution { public int minTrioDegree(int n, int[][] edges) { Map<Integer, Set<Integer>> map = new HashMap<Integer, Set<Integer>>(); for (int[] edge : edges) { int node0 = edge[0], node1 = edge[1]; Set<Integer> set0 = map.getOrDefault(node0, new HashSet<Integer>()); Set<Integer> set1 = map.getOrDefault(node1, new HashSet<Integer>()); set0.add(node1); set1.add(node0); map.put(node0, set0); map.put(node1, set1); } int minDegree = Integer.MAX_VALUE; for (int i = 1; i <= n; i++) { Set<Integer> set = map.getOrDefault(i, new HashSet<Integer>()); if (set.size() < 2) continue; List<Integer> list = new ArrayList<Integer>(set); int size = list.size(); for (int j = 0; j < size; j++) { int node1 = list.get(j); Set<Integer> set1 = map.get(node1); for (int k = j + 1; k < size; k++) { int node2 = list.get(k); if (set1.contains(node2)) { Set<Integer> set2 = map.get(node2); int count = set.size() + set1.size() + set2.size() - 6; minDegree = Math.min(minDegree, count); } } } } return minDegree == Integer.MAX_VALUE ? -1 : minDegree; } } ############ class Solution { public int minTrioDegree(int n, int[][] edges) { boolean[][] g = new boolean[n][n]; int[] deg = new int[n]; for (var e : edges) { int u = e[0] - 1, v = e[1] - 1; g[u][v] = true; g[v][u] = true; ++deg[u]; ++deg[v]; } int ans = 1 << 30; for (int i = 0; i < n; ++i) { for (int j = i + 1; j < n; ++j) { if (g[i][j]) { for (int k = j + 1; k < n; ++k) { if (g[i][k] && g[j][k]) { ans = Math.min(ans, deg[i] + deg[j] + deg[k] - 6); } } } } } return ans == 1 << 30 ? -1 : ans; } } -
class Solution: def minTrioDegree(self, n: int, edges: List[List[int]]) -> int: g = [[False] * n for _ in range(n)] deg = [0] * n for u, v in edges: u, v = u - 1, v - 1 g[u][v] = g[v][u] = True deg[u] += 1 deg[v] += 1 ans = inf for i in range(n): for j in range(i + 1, n): if g[i][j]: for k in range(j + 1, n): if g[i][k] and g[j][k]: ans = min(ans, deg[i] + deg[j] + deg[k] - 6) return -1 if ans == inf else ans -
class Solution { public: int minTrioDegree(int n, vector<vector<int>>& edges) { bool g[n][n]; memset(g, 0, sizeof g); int deg[n]; memset(deg, 0, sizeof deg); for (auto& e : edges) { int u = e[0] - 1, v = e[1] - 1; g[u][v] = g[v][u] = true; deg[u]++, deg[v]++; } int ans = INT_MAX; for (int i = 0; i < n; ++i) { for (int j = i + 1; j < n; ++j) { if (g[i][j]) { for (int k = j + 1; k < n; ++k) { if (g[j][k] && g[i][k]) { ans = min(ans, deg[i] + deg[j] + deg[k] - 6); } } } } } return ans == INT_MAX ? -1 : ans; } }; -
func minTrioDegree(n int, edges [][]int) int { g := make([][]bool, n) deg := make([]int, n) for i := range g { g[i] = make([]bool, n) } for _, e := range edges { u, v := e[0]-1, e[1]-1 g[u][v], g[v][u] = true, true deg[u]++ deg[v]++ } ans := 1 << 30 for i := 0; i < n; i++ { for j := i + 1; j < n; j++ { if g[i][j] { for k := j + 1; k < n; k++ { if g[i][k] && g[j][k] { ans = min(ans, deg[i]+deg[j]+deg[k]-6) } } } } } if ans == 1<<30 { return -1 } return ans } func min(a, b int) int { if a < b { return a } return b } -
function minTrioDegree(n: number, edges: number[][]): number { const g = Array.from({ length: n }, () => Array(n).fill(false)); const deg: number[] = Array(n).fill(0); for (let [u, v] of edges) { u--; v--; g[u][v] = g[v][u] = true; ++deg[u]; ++deg[v]; } let ans = Infinity; for (let i = 0; i < n; ++i) { for (let j = i + 1; j < n; ++j) { if (g[i][j]) { for (let k = j + 1; k < n; ++k) { if (g[i][k] && g[j][k]) { ans = Math.min(ans, deg[i] + deg[j] + deg[k] - 6); } } } } } return ans === Infinity ? -1 : ans; }