1761. Minimum Degree of a Connected Trio in a Graph

You are given an undirected graph. You are given an integer n which is the number of nodes in the graph and an array edges, where each edges[i] = [ui, vi] indicates that there is an undirected edge between ui and vi.

A connected trio is a set of three nodes where there is an edge between every pair of them.

The degree of a connected trio is the number of edges where one endpoint is in the trio, and the other is not.

Return the minimum degree of a connected trio in the graph, or -1 if the graph has no connected trios.

Example 1:

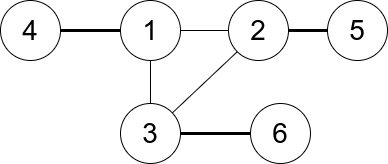
Input: n = 6, edges = [[1,2],[1,3],[3,2],[4,1],[5,2],[3,6]]
Output: 3
Explanation: There is exactly one trio, which is [1,2,3]. The edges that form its degree are bolded in the figure above.

Example 2:

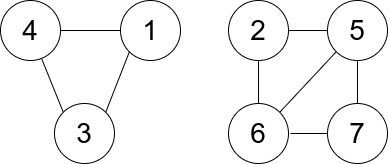
Input: n = 7, edges = [[1,3],[4,1],[4,3],[2,5],[5,6],[6,7],[7,5],[2,6]]
Output: 0
Explanation: There are exactly three trios:
1) [1,4,3] with degree 0.
2) [2,5,6] with degree 2.
3) [5,6,7] with degree 2.

Constraints:

• 2 <= n <= 400
• edges[i].length == 2
• 1 <= edges.length <= n * (n-1) / 2
• 1 <= ui, vi <= n
• ui != vi
• There are no repeated edges.