Welcome to Subscribe On Youtube

Formatted question description: https://leetcode.ca/all/1739.html

1739. Building Boxes

Level

Hard

Description

You have a cubic storeroom where the width, length, and height of the room are all equal to n units. You are asked to place n boxes in this room where each box is a cube of unit side length. There are however some rules to placing the boxes:

• You can place the boxes anywhere on the floor.
• If box x is placed on top of the box y, then each side of the four vertical sides of the box y must either be adjacent to another box or to a wall.

Given an integer n, return the minimum possible number of boxes touching the floor.

Example 1:

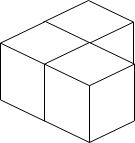
Input: n = 3

Output: 3

Explanation: The figure above is for the placement of the three boxes.

These boxes are placed in the corner of the room, where the corner is on the left side.

Example 2:

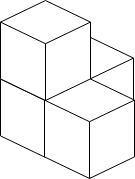
Input: n = 4

Output: 3

Explanation: The figure above is for the placement of the four boxes. These boxes are placed in the corner of the room, where the corner is on the left side.

Example 3:

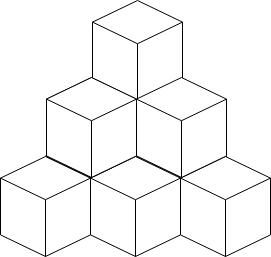
Input: n = 10

Output: 6

Explanation: The figure above is for the placement of the ten boxes.

These boxes are placed in the corner of the room, where the corner is on the back side.

Constraints:

• 1 <= n <= 10^9

Solution

The ideal situation is that the i-th level from the top (where i starts from 1) contains i * (i + 1) / 2 boxes. Calculate the minimum number of boxes under the ideal situation such that the number of boxes is at least n. After that, calculate the remaining boxes at the bottom level where the number of boxes is exactly n. Let remain be the number of remaining boxes. Find the minimum possible value min such that min * (min + 1) / 2 >= remain. Let currLevel be the number of boxes in the last level just above the bottom level. The result is currLevel + min.

• Java
• C++
• Python
• Go

• class Solution {
      public int minimumBoxes(int n) {
          if (n <= 3)
              return n;
          int total = 0;
          int levelCount = 0;
          int currLevel = 0;
          while (total < n) {
              levelCount++;
              currLevel += levelCount;
              total += currLevel;
          }
          if (total == n)
              return currLevel;
          total -= currLevel;
          currLevel -= levelCount;
          int remain = n - total;
          int increase = findMin(remain);
          return currLevel + increase;
      }
  
      public int findMin(int remain) {
          int min = (int) Math.sqrt(remain * 2);
          while (min * (min + 1) / 2 < remain)
              min++;
          return min;
      }
  }
  
  ############
  
  class Solution {
      public int minimumBoxes(int n) {
          int s = 0, k = 1;
          while (s + k * (k + 1) / 2 <= n) {
              s += k * (k + 1) / 2;
              ++k;
          }
          --k;
          int ans = k * (k + 1) / 2;
          k = 1;
          while (s < n) {
              ++ans;
              s += k;
              ++k;
          }
          return ans;
      }
  }
  

• // OJ: https://leetcode.com/problems/building-boxes/
  class Solution {
  public:
      int minimumBoxes(int n) {
          int bottom = 1, total = 1, h = 1;
          while (total + bottom + h + 1 <= n) {
              bottom += ++h;
              total += bottom;
          }
          int r = n - total, L = 0, R = h + 1;
          while (L <= R) {
              int M = (L + R) / 2;
              if ((1 + M) * M / 2 >= r) R = M - 1;
              else L = M + 1;
          }
          return bottom + L;
      }
  };
  

• class Solution:
      def minimumBoxes(self, n: int) -> int:
          s, k = 0, 1
          while s + k * (k + 1) // 2 <= n:
              s += k * (k + 1) // 2
              k += 1
          k -= 1
          ans = k * (k + 1) // 2
          k = 1
          while s < n:
              ans += 1
              s += k
              k += 1
          return ans
  
  
  

• func minimumBoxes(n int) int {
  	s, k := 0, 1
  	for s+k*(k+1)/2 <= n {
  		s += k * (k + 1) / 2
  		k++
  	}
  	k--
  	ans := k * (k + 1) / 2
  	k = 1
  	for s < n {
  		ans++
  		s += k
  		k++
  	}
  	return ans
  }
  

All Problems

All Solutions