Welcome to Subscribe On Youtube
1902. Depth of BST Given Insertion Order
Description
You are given a 0-indexed integer array order of length n, a permutation of integers from 1 to n representing the order of insertion into a binary search tree.
A binary search tree is defined as follows:
- The left subtree of a node contains only nodes with keys less than the node's key.
- The right subtree of a node contains only nodes with keys greater than the node's key.
- Both the left and right subtrees must also be binary search trees.
The binary search tree is constructed as follows:
order[0]will be the root of the binary search tree.- All subsequent elements are inserted as the child of any existing node such that the binary search tree properties hold.
Return the depth of the binary search tree.
A binary tree's depth is the number of nodes along the longest path from the root node down to the farthest leaf node.
Example 1:

Input: order = [2,1,4,3] Output: 3 Explanation: The binary search tree has a depth of 3 with path 2->3->4.
Example 2:
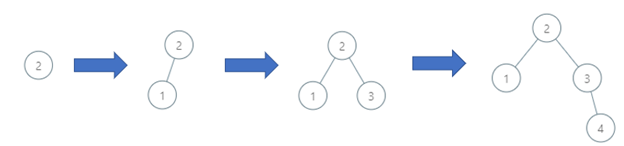
Input: order = [2,1,3,4] Output: 3 Explanation: The binary search tree has a depth of 3 with path 2->3->4.
Example 3:
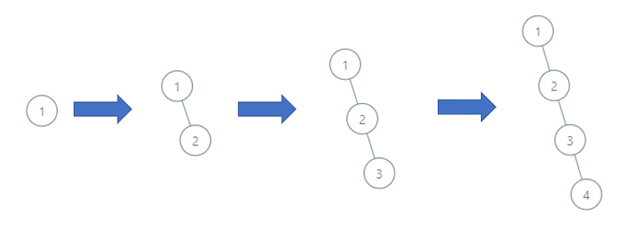
Input: order = [1,2,3,4] Output: 4 Explanation: The binary search tree has a depth of 4 with path 1->2->3->4.
Constraints:
n == order.length1 <= n <= 105orderis a permutation of integers between1andn.
Solutions
-
class Solution { public int maxDepthBST(int[] order) { TreeMap<Integer, Integer> tm = new TreeMap<>(); tm.put(0, 0); tm.put(Integer.MAX_VALUE, 0); tm.put(order[0], 1); int ans = 1; for (int i = 1; i < order.length; ++i) { int v = order[i]; Map.Entry<Integer, Integer> lower = tm.lowerEntry(v); Map.Entry<Integer, Integer> higher = tm.higherEntry(v); int depth = 1 + Math.max(lower.getValue(), higher.getValue()); ans = Math.max(ans, depth); tm.put(v, depth); } return ans; } } -
from sortedcontainers import SortedDict class Solution: def maxDepthBST(self, order: List[int]) -> int: sd = SortedDict({0: 0, inf: 0, order[0]: 1}) ans = 1 for v in order[1:]: lower = sd.bisect_left(v) - 1 higher = lower + 1 depth = 1 + max(sd.values()[lower], sd.values()[higher]) ans = max(ans, depth) sd[v] = depth return ans