Welcome to Subscribe On Youtube
1901. Find a Peak Element II
Description
A peak element in a 2D grid is an element that is strictly greater than all of its adjacent neighbors to the left, right, top, and bottom.
Given a 0-indexed m x n matrix mat where no two adjacent cells are equal, find any peak element mat[i][j] and return the length 2 array [i,j].
You may assume that the entire matrix is surrounded by an outer perimeter with the value -1 in each cell.
You must write an algorithm that runs in O(m log(n)) or O(n log(m)) time.
Example 1:

Input: mat = [[1,4],[3,2]] Output: [0,1] Explanation: Both 3 and 4 are peak elements so [1,0] and [0,1] are both acceptable answers.
Example 2:
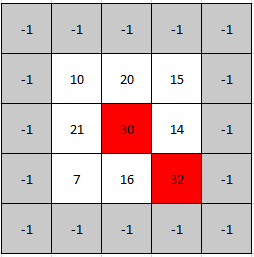
Input: mat = [[10,20,15],[21,30,14],[7,16,32]] Output: [1,1] Explanation: Both 30 and 32 are peak elements so [1,1] and [2,2] are both acceptable answers.
Constraints:
m == mat.lengthn == mat[i].length1 <= m, n <= 5001 <= mat[i][j] <= 105- No two adjacent cells are equal.
Solutions
Solution 1: Binary Search
Let $m$ and $n$ be the number of rows and columns of the matrix, respectively.
The problem asks us to find a peak, and the time complexity should be $O(m \times \log n)$ or $O(n \times \log m)$. Therefore, we can consider using binary search.
We consider the maximum value of the $i$-th row, and denote its index as $j$.
If $mat[i][j] > mat[i + 1][j]$, then there must be a peak in the rows $[0,..i]$. We only need to find the maximum value in these rows. Similarly, if $mat[i][j] < mat[i + 1][j]$, then there must be a peak in the rows $[i + 1,..m - 1]$. We only need to find the maximum value in these rows.
Why is the above method correct? We can prove it by contradiction.
If $mat[i][j] > mat[i + 1][j]$, suppose there is no peak in the rows $[0,..i]$. Then $mat[i][j]$ is not a peak. Since $mat[i][j]$ is the maximum value of the $i$-th row, and $mat[i][j] > mat[i + 1][j]$, then $mat[i][j] < mat[i - 1][j]$. We continue to consider from the $(i - 1)$-th row upwards, and the maximum value of each row is less than the maximum value of the previous row. When we traverse to $i = 0$, since all elements in the matrix are positive integers, and the values of the cells around the matrix are $-1$. Therefore, at the 0-th row, its maximum value is greater than all its adjacent elements, so the maximum value of the 0-th row is a peak, which contradicts the assumption. Therefore, there must be a peak in the rows $[0,..i]$.
For the case where $mat[i][j] < mat[i + 1][j]$, we can prove in a similar way that there must be a peak in the rows $[i + 1,..m - 1]$.
Therefore, we can use binary search to find the peak.
We perform binary search on the rows of the matrix, initially with the search boundaries $l = 0$, $r = m - 1$. Each time, we find the middle row $mid$ and find the index $j$ of the maximum value of this row. If $mat[mid][j] > mat[mid + 1][j]$, then we search for the peak in the rows $[0,..mid]$, i.e., update $r = mid$. Otherwise, we search for the peak in the rows $[mid + 1,..m - 1]$, i.e., update $l = mid + 1$. When $l = r$, we find the position $[l, j_l]$ of the peak, where $j_l$ is the index of the maximum value of the $l$-th row.
The time complexity is $O(n \times \log m)$, where $m$ and $n$ are the number of rows and columns of the matrix, respectively. The time complexity of binary search is $O(\log m)$, and each time we perform binary search, we need to traverse all elements of the $mid$-th row, with a time complexity of $O(n)$. The space complexity is $O(1)$.
-
class Solution { public int[] findPeakGrid(int[][] mat) { int l = 0, r = mat.length - 1; int n = mat[0].length; while (l < r) { int mid = (l + r) >> 1; int j = maxPos(mat[mid]); if (mat[mid][j] > mat[mid + 1][j]) { r = mid; } else { l = mid + 1; } } return new int[] {l, maxPos(mat[l])}; } private int maxPos(int[] arr) { int j = 0; for (int i = 1; i < arr.length; ++i) { if (arr[j] < arr[i]) { j = i; } } return j; } } -
class Solution { public: vector<int> findPeakGrid(vector<vector<int>>& mat) { int l = 0, r = mat.size() - 1; while (l < r) { int mid = (l + r) >> 1; int j = distance(mat[mid].begin(), max_element(mat[mid].begin(), mat[mid].end())); if (mat[mid][j] > mat[mid + 1][j]) { r = mid; } else { l = mid + 1; } } int j = distance(mat[l].begin(), max_element(mat[l].begin(), mat[l].end())); return {l, j}; } }; -
class Solution: def findPeakGrid(self, mat: List[List[int]]) -> List[int]: l, r = 0, len(mat) - 1 while l < r: mid = (l + r) >> 1 j = mat[mid].index(max(mat[mid])) if mat[mid][j] > mat[mid + 1][j]: r = mid else: l = mid + 1 return [l, mat[l].index(max(mat[l]))] -
func findPeakGrid(mat [][]int) []int { maxPos := func(arr []int) int { j := 0 for i := 1; i < len(arr); i++ { if arr[i] > arr[j] { j = i } } return j } l, r := 0, len(mat)-1 for l < r { mid := (l + r) >> 1 j := maxPos(mat[mid]) if mat[mid][j] > mat[mid+1][j] { r = mid } else { l = mid + 1 } } return []int{l, maxPos(mat[l])} } -
function findPeakGrid(mat: number[][]): number[] { let [l, r] = [0, mat.length - 1]; while (l < r) { const mid = (l + r) >> 1; const j = mat[mid].indexOf(Math.max(...mat[mid])); if (mat[mid][j] > mat[mid + 1][j]) { r = mid; } else { l = mid + 1; } } return [l, mat[l].indexOf(Math.max(...mat[l]))]; } -
impl Solution { pub fn find_peak_grid(mat: Vec<Vec<i32>>) -> Vec<i32> { let mut l: usize = 0; let mut r: usize = mat.len() - 1; while l < r { let mid: usize = (l + r) >> 1; let j: usize = mat[mid] .iter() .position(|&x| x == *mat[mid].iter().max().unwrap()) .unwrap(); if mat[mid][j] > mat[mid + 1][j] { r = mid; } else { l = mid + 1; } } let j: usize = mat[l] .iter() .position(|&x| x == *mat[l].iter().max().unwrap()) .unwrap(); vec![l as i32, j as i32] } }