1824. Minimum Sideway Jumps

Description

There is a 3 lane road of length n that consists of n + 1 points labeled from 0 to n. A frog starts at point 0 in the second lane and wants to jump to point n. However, there could be obstacles along the way.

You are given an array obstacles of length n + 1 where each obstacles[i] (ranging from 0 to 3) describes an obstacle on the lane obstacles[i] at point i. If obstacles[i] == 0, there are no obstacles at point i. There will be at most one obstacle in the 3 lanes at each point.

For example, if obstacles[2] == 1, then there is an obstacle on lane 1 at point 2.

The frog can only travel from point i to point i + 1 on the same lane if there is not an obstacle on the lane at point i + 1. To avoid obstacles, the frog can also perform a side jump to jump to another lane (even if they are not adjacent) at the same point if there is no obstacle on the new lane.

For example, the frog can jump from lane 3 at point 3 to lane 1 at point 3.

Return the minimum number of side jumps the frog needs to reach any lane at point n starting from lane 2 at point 0.

Note: There will be no obstacles on points 0 and n.

Example 1:

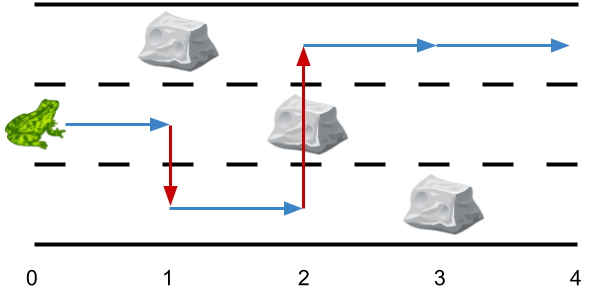
Input: obstacles = [0,1,2,3,0]
Output: 2 
Explanation: The optimal solution is shown by the arrows above. There are 2 side jumps (red arrows).
Note that the frog can jump over obstacles only when making side jumps (as shown at point 2).

Example 2:

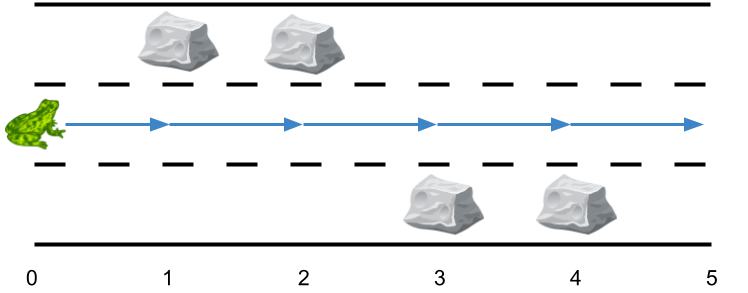
Input: obstacles = [0,1,1,3,3,0]
Output: 0
Explanation: There are no obstacles on lane 2. No side jumps are required.

Example 3:

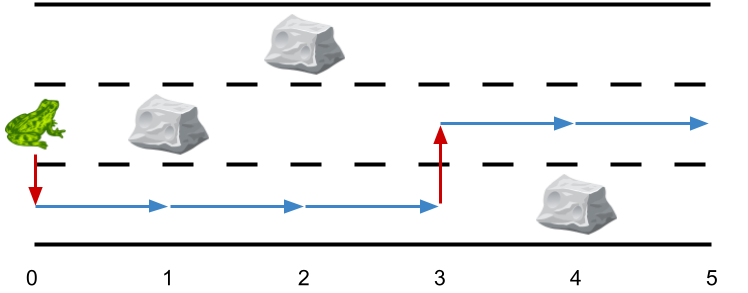
Input: obstacles = [0,2,1,0,3,0]
Output: 2
Explanation: The optimal solution is shown by the arrows above. There are 2 side jumps.

Constraints:

obstacles.length == n + 1
1 <= n <= 5 * 10⁵
0 <= obstacles[i] <= 3
obstacles[0] == obstacles[n] == 0

Solutions

Solution 1: Dynamic Programming

We define $f[i][j]$ as the minimum number of sidesteps for the frog to reach the $i$-th point and be on the $j$-th lane (index starts from $0$).

Note that the frog starts on the second lane (the problem index starts from $1$), so the value of $f[0][1]$ is $0$, and the values of $f[0][0]$ and $f[0][2]$ are both $1$. The answer is $min(f[n][0], f[n][1], f[n][2])$.

For each position $i$ from $1$ to $n$, we can enumerate the current lane $j$ of the frog. If $obstacles[i] = j + 1$, it means that there is an obstacle on the $j$-th lane, and the value of $f[i][j]$ is infinity. Otherwise, the frog can choose not to jump, in which case the value of $f[i][j]$ is $f[i - 1][j]$, or the frog can sidestep from other lanes, in which case $f[i][j] = min(f[i][j], min(f[i][0], f[i][1], f[i][2]) + 1)$.

In the code implementation, we can optimize the first dimension of space and only use an array $f$ of length $3$ for maintenance.

The time complexity is $O(n)$, where $n$ is the length of the array $obstacles$. The space complexity is $O(1)$.

class Solution {
    public int minSideJumps(int[] obstacles) {
        final int inf = 1 << 30;
        int[] f = {1, 0, 1};
        for (int i = 1; i < obstacles.length; ++i) {
            for (int j = 0; j < 3; ++j) {
                if (obstacles[i] == j + 1) {
                    f[j] = inf;
                    break;
                }
            }
            int x = Math.min(f[0], Math.min(f[1], f[2])) + 1;
            for (int j = 0; j < 3; ++j) {
                if (obstacles[i] != j + 1) {
                    f[j] = Math.min(f[j], x);
                }
            }
        }
        return Math.min(f[0], Math.min(f[1], f[2]));
    }
}

class Solution {
public:
    int minSideJumps(vector<int>& obstacles) {
        const int inf = 1 << 30;
        int f[3] = {1, 0, 1};
        for (int i = 1; i < obstacles.size(); ++i) {
            for (int j = 0; j < 3; ++j) {
                if (obstacles[i] == j + 1) {
                    f[j] = inf;
                    break;
                }
            }
            int x = min({f[0], f[1], f[2]}) + 1;
            for (int j = 0; j < 3; ++j) {
                if (obstacles[i] != j + 1) {
                    f[j] = min(f[j], x);
                }
            }
        }
        return min({f[0], f[1], f[2]});
    }
};

class Solution:
    def minSideJumps(self, obstacles: List[int]) -> int:
        f = [1, 0, 1]
        for v in obstacles[1:]:
            for j in range(3):
                if v == j + 1:
                    f[j] = inf
                    break
            x = min(f) + 1
            for j in range(3):
                if v != j + 1:
                    f[j] = min(f[j], x)
        return min(f)

func minSideJumps(obstacles []int) int {
	f := [3]int{1, 0, 1}
	const inf = 1 << 30
	for _, v := range obstacles[1:] {
		for j := 0; j < 3; j++ {
			if v == j+1 {
				f[j] = inf
				break
			}
		}
		x := min(f[0], min(f[1], f[2])) + 1
		for j := 0; j < 3; j++ {
			if v != j+1 {
				f[j] = min(f[j], x)
			}
		}
	}
	return min(f[0], min(f[1], f[2]))
}

function minSideJumps(obstacles: number[]): number {
    const inf = 1 << 30;
    const f = [1, 0, 1];
    for (let i = 1; i < obstacles.length; ++i) {
        for (let j = 0; j < 3; ++j) {
            if (obstacles[i] == j + 1) {
                f[j] = inf;
                break;
            }
        }
        const x = Math.min(...f) + 1;
        for (let j = 0; j < 3; ++j) {
            if (obstacles[i] != j + 1) {
                f[j] = Math.min(f[j], x);
            }
        }
    }
    return Math.min(...f);
}

1824 - Minimum Sideway Jumps

1824. Minimum Sideway Jumps

Description

Solutions

All Problems

All Solutions

Welcome to Subscribe On Youtube

1824. Minimum Sideway Jumps

Description

Solutions

All Problems

All Solutions