Welcome to Subscribe On Youtube
1706. Where Will the Ball Fall
Description
You have a 2-D grid of size m x n representing a box, and you have n balls. The box is open on the top and bottom sides.
Each cell in the box has a diagonal board spanning two corners of the cell that can redirect a ball to the right or to the left.
- A board that redirects the ball to the right spans the top-left corner to the bottom-right corner and is represented in the grid as
1. - A board that redirects the ball to the left spans the top-right corner to the bottom-left corner and is represented in the grid as
-1.
We drop one ball at the top of each column of the box. Each ball can get stuck in the box or fall out of the bottom. A ball gets stuck if it hits a "V" shaped pattern between two boards or if a board redirects the ball into either wall of the box.
Return an array answer of size n where answer[i] is the column that the ball falls out of at the bottom after dropping the ball from the ith column at the top, or -1 if the ball gets stuck in the box.
Example 1:
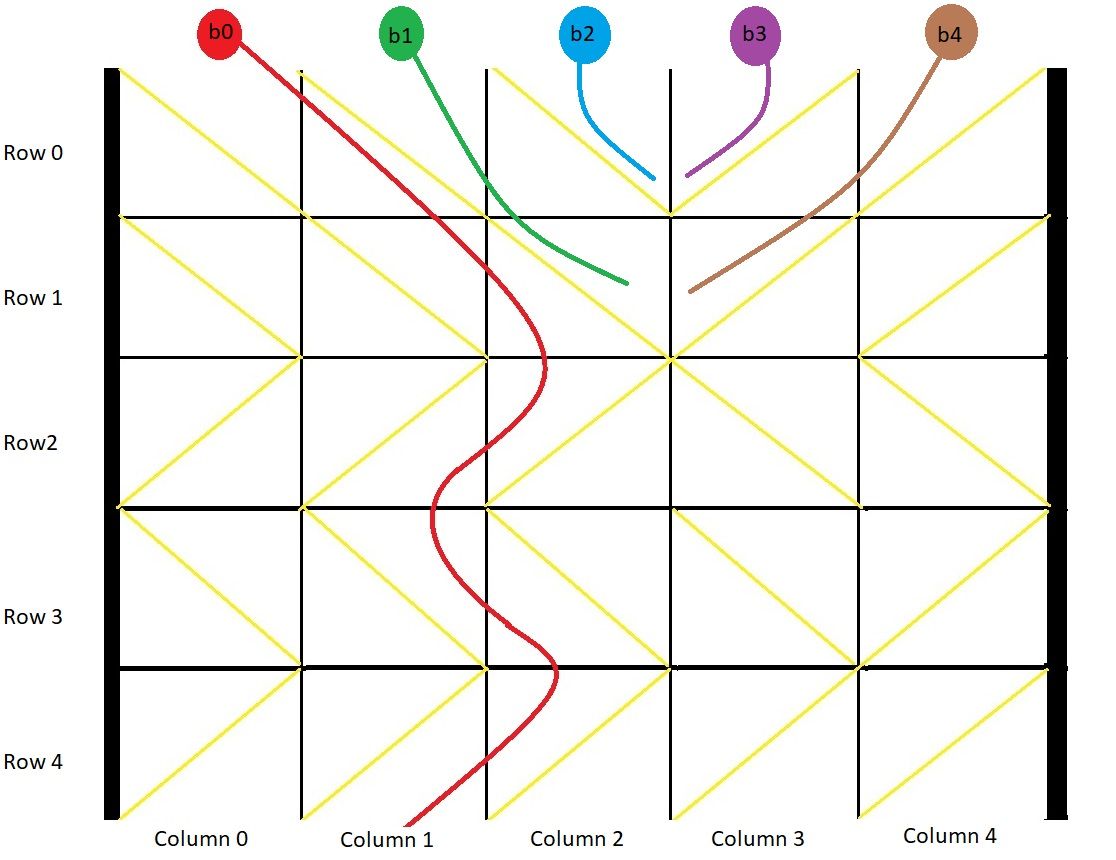
Input: grid = [[1,1,1,-1,-1],[1,1,1,-1,-1],[-1,-1,-1,1,1],[1,1,1,1,-1],[-1,-1,-1,-1,-1]] Output: [1,-1,-1,-1,-1] Explanation: This example is shown in the photo. Ball b0 is dropped at column 0 and falls out of the box at column 1. Ball b1 is dropped at column 1 and will get stuck in the box between column 2 and 3 and row 1. Ball b2 is dropped at column 2 and will get stuck on the box between column 2 and 3 and row 0. Ball b3 is dropped at column 3 and will get stuck on the box between column 2 and 3 and row 0. Ball b4 is dropped at column 4 and will get stuck on the box between column 2 and 3 and row 1.
Example 2:
Input: grid = [[-1]] Output: [-1] Explanation: The ball gets stuck against the left wall.
Example 3:
Input: grid = [[1,1,1,1,1,1],[-1,-1,-1,-1,-1,-1],[1,1,1,1,1,1],[-1,-1,-1,-1,-1,-1]] Output: [0,1,2,3,4,-1]
Constraints:
m == grid.lengthn == grid[i].length1 <= m, n <= 100grid[i][j]is1or-1.
Solutions
Solution 1: Case Discussion + DFS
We can use DFS to simulate the movement of the ball. We design a function $dfs(i, j)$, which represents that the ball starts from the $i$th row and the $j$th column, and finally falls in which column. The ball will get stuck in the following situations:
- The ball is in the leftmost column, and the cell’s vane directs the ball to the left.
- The ball is in the rightmost column, and the cell’s vane directs the ball to the right.
- The cell’s vane where the ball is located directs the ball to the right, and the vane of the cell adjacent to the right of the ball directs the ball to the left.
- The cell’s vane where the ball is located directs the ball to the left, and the vane of the cell adjacent to the left of the ball directs the ball to the right.
If any of the above situations are met, we can judge that the ball will get stuck and return $-1$. Otherwise, we can continue to recursively find the next position of the ball. Finally, if the ball reaches the last row, we can return the current column number.
The time complexity is $O(m \times n)$, and the space complexity is $O(m)$. Where $m$ and $n$ are the number of rows and columns of the array $grid$, respectively.
-
class Solution { private int m; private int n; private int[][] grid; public int[] findBall(int[][] grid) { m = grid.length; n = grid[0].length; this.grid = grid; int[] ans = new int[n]; for (int j = 0; j < n; ++j) { ans[j] = dfs(0, j); } return ans; } private int dfs(int i, int j) { if (i == m) { return j; } if (j == 0 && grid[i][j] == -1) { return -1; } if (j == n - 1 && grid[i][j] == 1) { return -1; } if (grid[i][j] == 1 && grid[i][j + 1] == -1) { return -1; } if (grid[i][j] == -1 && grid[i][j - 1] == 1) { return -1; } return grid[i][j] == 1 ? dfs(i + 1, j + 1) : dfs(i + 1, j - 1); } } -
class Solution { public: vector<int> findBall(vector<vector<int>>& grid) { int m = grid.size(), n = grid[0].size(); vector<int> ans(n); function<int(int, int)> dfs = [&](int i, int j) { if (i == m) { return j; } if (j == 0 && grid[i][j] == -1) { return -1; } if (j == n - 1 && grid[i][j] == 1) { return -1; } if (grid[i][j] == 1 && grid[i][j + 1] == -1) { return -1; } if (grid[i][j] == -1 && grid[i][j - 1] == 1) { return -1; } return grid[i][j] == 1 ? dfs(i + 1, j + 1) : dfs(i + 1, j - 1); }; for (int j = 0; j < n; ++j) { ans[j] = dfs(0, j); } return ans; } }; -
class Solution: def findBall(self, grid: List[List[int]]) -> List[int]: def dfs(i: int, j: int) -> int: if i == m: return j if j == 0 and grid[i][j] == -1: return -1 if j == n - 1 and grid[i][j] == 1: return -1 if grid[i][j] == 1 and grid[i][j + 1] == -1: return -1 if grid[i][j] == -1 and grid[i][j - 1] == 1: return -1 return dfs(i + 1, j + 1) if grid[i][j] == 1 else dfs(i + 1, j - 1) m, n = len(grid), len(grid[0]) return [dfs(0, j) for j in range(n)] -
func findBall(grid [][]int) (ans []int) { m, n := len(grid), len(grid[0]) var dfs func(i, j int) int dfs = func(i, j int) int { if i == m { return j } if j == 0 && grid[i][j] == -1 { return -1 } if j == n-1 && grid[i][j] == 1 { return -1 } if grid[i][j] == 1 && grid[i][j+1] == -1 { return -1 } if grid[i][j] == -1 && grid[i][j-1] == 1 { return -1 } if grid[i][j] == 1 { return dfs(i+1, j+1) } return dfs(i+1, j-1) } for j := 0; j < n; j++ { ans = append(ans, dfs(0, j)) } return } -
function findBall(grid: number[][]): number[] { const m = grid.length; const n = grid[0].length; const dfs = (i: number, j: number) => { if (i === m) { return j; } if (grid[i][j] === 1) { if (j === n - 1 || grid[i][j + 1] === -1) { return -1; } return dfs(i + 1, j + 1); } else { if (j === 0 || grid[i][j - 1] === 1) { return -1; } return dfs(i + 1, j - 1); } }; const ans: number[] = []; for (let j = 0; j < n; ++j) { ans.push(dfs(0, j)); } return ans; } -
impl Solution { fn dfs(grid: &Vec<Vec<i32>>, i: usize, j: usize) -> i32 { if i == grid.len() { return j as i32; } if grid[i][j] == 1 { if j == grid[0].len() - 1 || grid[i][j + 1] == -1 { return -1; } Self::dfs(grid, i + 1, j + 1) } else { if j == 0 || grid[i][j - 1] == 1 { return -1; } Self::dfs(grid, i + 1, j - 1) } } pub fn find_ball(grid: Vec<Vec<i32>>) -> Vec<i32> { let m = grid.len(); let n = grid[0].len(); let mut res = vec![0; n]; for i in 0..n { res[i] = Self::dfs(&grid, 0, i); } res } } -
/** * @param {number[][]} grid * @return {number[]} */ var findBall = function (grid) { const m = grid.length; const n = grid[0].length; const dfs = (i, j) => { if (i === m) { return j; } if (grid[i][j] === 1) { if (j === n - 1 || grid[i][j + 1] === -1) { return -1; } return dfs(i + 1, j + 1); } else { if (j === 0 || grid[i][j - 1] === 1) { return -1; } return dfs(i + 1, j - 1); } }; return Array.from({ length: n }, (_, j) => dfs(0, j)); };