1697. Checking Existence of Edge Length Limited Paths

Description

An undirected graph of n nodes is defined by edgeList, where edgeList[i] = [u_i, v_i, dis_i] denotes an edge between nodes u_i and v_i with distance dis_i. Note that there may be multiple edges between two nodes.

Given an array queries, where queries[j] = [p_j, q_j, limit_j], your task is to determine for each queries[j] whether there is a path between p_j and q_jsuch that each edge on the path has a distance strictly less than limit_j .

Return a boolean array answer, where answer.length == queries.length and the j^th value of answer is true if there is a path for queries[j] is true, and false otherwise.

Example 1:

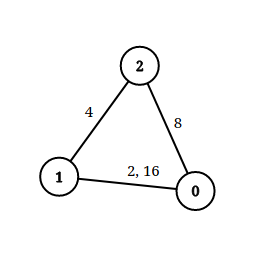
Input: n = 3, edgeList = [[0,1,2],[1,2,4],[2,0,8],[1,0,16]], queries = [[0,1,2],[0,2,5]]
Output: [false,true]
Explanation: The above figure shows the given graph. Note that there are two overlapping edges between 0 and 1 with distances 2 and 16.
For the first query, between 0 and 1 there is no path where each distance is less than 2, thus we return false for this query.
For the second query, there is a path (0 -> 1 -> 2) of two edges with distances less than 5, thus we return true for this query.

Example 2:

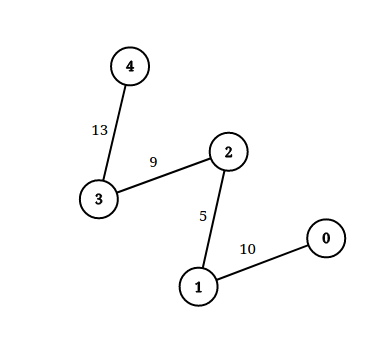
Input: n = 5, edgeList = [[0,1,10],[1,2,5],[2,3,9],[3,4,13]], queries = [[0,4,14],[1,4,13]]
Output: [true,false]
Explanation: The above figure shows the given graph.

Constraints:

2 <= n <= 10⁵
1 <= edgeList.length, queries.length <= 10⁵
edgeList[i].length == 3
queries[j].length == 3
0 <= u_i, v_i, p_j, q_j <= n - 1
u_i != v_i
p_j != q_j
1 <= dis_i, limit_j <= 10⁹
There may be multiple edges between two nodes.

Solutions

Union find.

class Solution {
    private int[] p;

    public boolean[] distanceLimitedPathsExist(int n, int[][] edgeList, int[][] queries) {
        p = new int[n];
        for (int i = 0; i < n; ++i) {
            p[i] = i;
        }
        Arrays.sort(edgeList, (a, b) -> a[2] - b[2]);
        int m = queries.length;
        boolean[] ans = new boolean[m];
        Integer[] qid = new Integer[m];
        for (int i = 0; i < m; ++i) {
            qid[i] = i;
        }
        Arrays.sort(qid, (i, j) -> queries[i][2] - queries[j][2]);
        int j = 0;
        for (int i : qid) {
            int a = queries[i][0], b = queries[i][1], limit = queries[i][2];
            while (j < edgeList.length && edgeList[j][2] < limit) {
                int u = edgeList[j][0], v = edgeList[j][1];
                p[find(u)] = find(v);
                ++j;
            }
            ans[i] = find(a) == find(b);
        }
        return ans;
    }

    private int find(int x) {
        if (p[x] != x) {
            p[x] = find(p[x]);
        }
        return p[x];
    }
}

class Solution {
public:
    vector<bool> distanceLimitedPathsExist(int n, vector<vector<int>>& edgeList, vector<vector<int>>& queries) {
        vector<int> p(n);
        iota(p.begin(), p.end(), 0);
        sort(edgeList.begin(), edgeList.end(), [](auto& a, auto& b) { return a[2] < b[2]; });
        function<int(int)> find = [&](int x) -> int {
            if (p[x] != x) p[x] = find(p[x]);
            return p[x];
        };
        int m = queries.size();
        vector<bool> ans(m);
        vector<int> qid(m);
        iota(qid.begin(), qid.end(), 0);
        sort(qid.begin(), qid.end(), [&](int i, int j) { return queries[i][2] < queries[j][2]; });
        int j = 0;
        for (int i : qid) {
            int a = queries[i][0], b = queries[i][1], limit = queries[i][2];
            while (j < edgeList.size() && edgeList[j][2] < limit) {
                int u = edgeList[j][0], v = edgeList[j][1];
                p[find(u)] = find(v);
                ++j;
            }
            ans[i] = find(a) == find(b);
        }
        return ans;
    }
};

class Solution:
    def distanceLimitedPathsExist(
        self, n: int, edgeList: List[List[int]], queries: List[List[int]]
    ) -> List[bool]:
        def find(x):
            if p[x] != x:
                p[x] = find(p[x])
            return p[x]

        p = list(range(n))
        edgeList.sort(key=lambda x: x[2])
        j = 0
        ans = [False] * len(queries)
        for i, (a, b, limit) in sorted(enumerate(queries), key=lambda x: x[1][2]):
            while j < len(edgeList) and edgeList[j][2] < limit:
                u, v, _ = edgeList[j]
                p[find(u)] = find(v)
                j += 1
            ans[i] = find(a) == find(b)
        return ans

func distanceLimitedPathsExist(n int, edgeList [][]int, queries [][]int) []bool {
	p := make([]int, n)
	for i := range p {
		p[i] = i
	}
	sort.Slice(edgeList, func(i, j int) bool { return edgeList[i][2] < edgeList[j][2] })
	var find func(int) int
	find = func(x int) int {
		if p[x] != x {
			p[x] = find(p[x])
		}
		return p[x]
	}
	m := len(queries)
	qid := make([]int, m)
	ans := make([]bool, m)
	for i := range qid {
		qid[i] = i
	}
	sort.Slice(qid, func(i, j int) bool { return queries[qid[i]][2] < queries[qid[j]][2] })
	j := 0
	for _, i := range qid {
		a, b, limit := queries[i][0], queries[i][1], queries[i][2]
		for j < len(edgeList) && edgeList[j][2] < limit {
			u, v := edgeList[j][0], edgeList[j][1]
			p[find(u)] = find(v)
			j++
		}
		ans[i] = find(a) == find(b)
	}
	return ans
}

impl Solution {
    #[allow(dead_code)]
    pub fn distance_limited_paths_exist(
        n: i32,
        edge_list: Vec<Vec<i32>>,
        queries: Vec<Vec<i32>>
    ) -> Vec<bool> {
        let mut disjoint_set: Vec<usize> = vec![0; n as usize];
        let mut ans_vec: Vec<bool> = vec![false; queries.len()];
        let mut q_vec: Vec<usize> = vec![0; queries.len()];

        // Initialize the set
        for i in 0..n {
            disjoint_set[i as usize] = i as usize;
        }

        // Initialize the q_vec
        for i in 0..queries.len() {
            q_vec[i] = i;
        }

        // Sort the q_vec based on the query limit, from the lowest to highest
        q_vec.sort_by(|i, j| queries[*i][2].cmp(&queries[*j][2]));

        // Sort the edge_list based on the edge weight, from the lowest to highest
        let mut edge_list = edge_list.clone();
        edge_list.sort_by(|i, j| i[2].cmp(&j[2]));

        let mut edge_idx: usize = 0;
        for q_idx in &q_vec {
            let s = queries[*q_idx][0] as usize;
            let d = queries[*q_idx][1] as usize;
            let limit = queries[*q_idx][2];
            // Construct the disjoint set
            while edge_idx < edge_list.len() && edge_list[edge_idx][2] < limit {
                Solution::union(
                    edge_list[edge_idx][0] as usize,
                    edge_list[edge_idx][1] as usize,
                    &mut disjoint_set
                );
                edge_idx += 1;
            }
            // If the parents of s & d are the same, this query should be `true`
            // Otherwise, the current query is `false`
            ans_vec[*q_idx] = Solution::check_valid(s, d, &mut disjoint_set);
        }

        ans_vec
    }

    #[allow(dead_code)]
    pub fn find(x: usize, d_set: &mut Vec<usize>) -> usize {
        if d_set[x] != x {
            d_set[x] = Solution::find(d_set[x], d_set);
        }
        return d_set[x];
    }

    #[allow(dead_code)]
    pub fn union(s: usize, d: usize, d_set: &mut Vec<usize>) {
        let p_s = Solution::find(s, d_set);
        let p_d = Solution::find(d, d_set);
        d_set[p_s] = p_d;
    }

    #[allow(dead_code)]
    pub fn check_valid(s: usize, d: usize, d_set: &mut Vec<usize>) -> bool {
        let p_s = Solution::find(s, d_set);
        let p_d = Solution::find(d, d_set);
        p_s == p_d
    }
}

1697 - Checking Existence of Edge Length Limited Paths

1697. Checking Existence of Edge Length Limited Paths

Description

Solutions

All Problems

All Solutions

Welcome to Subscribe On Youtube

1697. Checking Existence of Edge Length Limited Paths

Description

Solutions

All Problems

All Solutions