Welcome to Subscribe On Youtube

1692. Count Ways to Distribute Candies

Description

There are n unique candies (labeled 1 through n) and k bags. You are asked to distribute all the candies into the bags such that every bag has at least one candy.

There can be multiple ways to distribute the candies. Two ways are considered different if the candies in one bag in the first way are not all in the same bag in the second way. The order of the bags and the order of the candies within each bag do not matter.

For example, (1), (2,3) and (2), (1,3) are considered different because candies 2 and 3 in the bag (2,3) in the first way are not in the same bag in the second way (they are split between the bags (2) and (1,3)). However, (1), (2,3) and (3,2), (1) are considered the same because the candies in each bag are all in the same bags in both ways.

Given two integers, n and k, return the number of different ways to distribute the candies. As the answer may be too large, return it modulo 109 + 7.

 

Example 1:

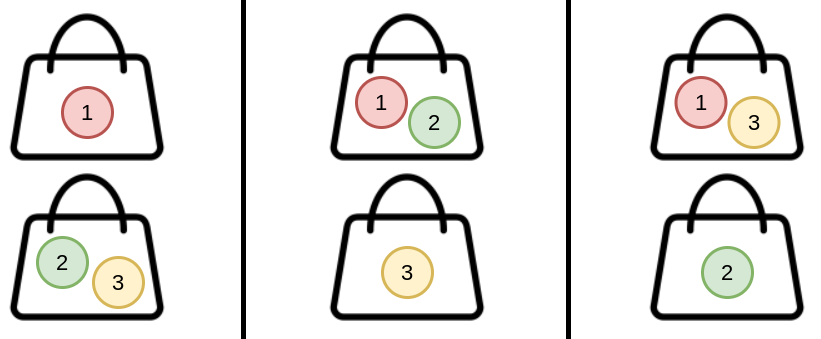
Input: n = 3, k = 2
Output: 3
Explanation: You can distribute 3 candies into 2 bags in 3 ways:
(1), (2,3)
(1,2), (3)
(1,3), (2)

Example 2:

Input: n = 4, k = 2
Output: 7
Explanation: You can distribute 4 candies into 2 bags in 7 ways:
(1), (2,3,4)
(1,2), (3,4)
(1,3), (2,4)
(1,4), (2,3)
(1,2,3), (4)
(1,2,4), (3)
(1,3,4), (2)

Example 3:

Input: n = 20, k = 5
Output: 206085257
Explanation: You can distribute 20 candies into 5 bags in 1881780996 ways. 1881780996 modulo 109 + 7 = 206085257.

 

Constraints:

• 1 <= k <= n <= 1000

Solutions

Solution 1: Dynamic Programming

We define $f[i][j]$ as the number of different ways to distribute $i$ candies to $j$ bags. Initially, $f[0][0]=1$, and the answer is $f[n][k]$.

We consider how to distribute the $i$-th candy. If the $i$-th candy is distributed to a new bag, then $f[i][j]=f[i-1][j-1]$. If the $i$-th candy is distributed to an existing bag, then $f[i][j]=f[i-1][j]\times j$. Therefore, the state transition equation is:

\[f[i][j]=f[i-1][j-1]+f[i-1][j]\times j\]

The final answer is $f[n][k]$.

The time complexity is $O(n \times k)$, and the space complexity is $O(n \times k)$. Here, $n$ and $k$ are the number of candies and bags, respectively.

• Java
• C++
• Python
• Go
• TypeScript

• class Solution {
      public int waysToDistribute(int n, int k) {
          final int mod = (int) 1e9 + 7;
          int[][] f = new int[n + 1][k + 1];
          f[0][0] = 1;
          for (int i = 1; i <= n; i++) {
              for (int j = 1; j <= k; j++) {
                  f[i][j] = (int) ((long) f[i - 1][j] * j % mod + f[i - 1][j - 1]) % mod;
              }
          }
          return f[n][k];
      }
  }
  

• class Solution {
  public:
      int waysToDistribute(int n, int k) {
          const int mod = 1e9 + 7;
          int f[n + 1][k + 1];
          memset(f, 0, sizeof(f));
          f[0][0] = 1;
          for (int i = 1; i <= n; ++i) {
              for (int j = 1; j <= k; ++j) {
                  f[i][j] = (1LL * f[i - 1][j] * j + f[i - 1][j - 1]) % mod;
              }
          }
          return f[n][k];
      }
  };
  

• class Solution:
      def waysToDistribute(self, n: int, k: int) -> int:
          mod = 10**9 + 7
          f = [[0] * (k + 1) for _ in range(n + 1)]
          f[0][0] = 1
          for i in range(1, n + 1):
              for j in range(1, k + 1):
                  f[i][j] = (f[i - 1][j] * j + f[i - 1][j - 1]) % mod
          return f[n][k]
  
  

• func waysToDistribute(n int, k int) int {
  	f := make([][]int, n+1)
  	for i := range f {
  		f[i] = make([]int, k+1)
  	}
  	f[0][0] = 1
  	const mod = 1e9 + 7
  	for i := 1; i <= n; i++ {
  		for j := 1; j <= k; j++ {
  			f[i][j] = (f[i-1][j]*j + f[i-1][j-1]) % mod
  		}
  	}
  	return f[n][k]
  }
  

• function waysToDistribute(n: number, k: number): number {
      const mod = 10 ** 9 + 7;
      const f: number[][] = Array.from({ length: n + 1 }, () =>
          Array.from({ length: k + 1 }, () => 0),
      );
      f[0][0] = 1;
      for (let i = 1; i <= n; ++i) {
          for (let j = 1; j <= k; ++j) {
              f[i][j] = (f[i - 1][j] * j + f[i - 1][j - 1]) % mod;
          }
      }
      return f[n][k];
  }
  
  

All Problems

All Solutions