Welcome to Subscribe On Youtube
1691. Maximum Height by Stacking Cuboids
Description
Given n cuboids where the dimensions of the ith cuboid is cuboids[i] = [widthi, lengthi, heighti] (0-indexed). Choose a subset of cuboids and place them on each other.
You can place cuboid i on cuboid j if widthi <= widthj and lengthi <= lengthj and heighti <= heightj. You can rearrange any cuboid's dimensions by rotating it to put it on another cuboid.
Return the maximum height of the stacked cuboids.
Example 1:
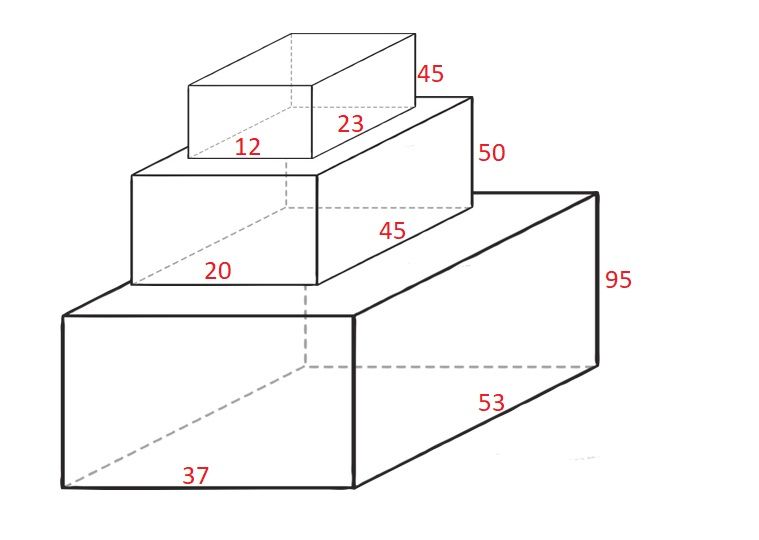
Input: cuboids = [[50,45,20],[95,37,53],[45,23,12]] Output: 190 Explanation: Cuboid 1 is placed on the bottom with the 53x37 side facing down with height 95. Cuboid 0 is placed next with the 45x20 side facing down with height 50. Cuboid 2 is placed next with the 23x12 side facing down with height 45. The total height is 95 + 50 + 45 = 190.
Example 2:
Input: cuboids = [[38,25,45],[76,35,3]] Output: 76 Explanation: You can't place any of the cuboids on the other. We choose cuboid 1 and rotate it so that the 35x3 side is facing down and its height is 76.
Example 3:
Input: cuboids = [[7,11,17],[7,17,11],[11,7,17],[11,17,7],[17,7,11],[17,11,7]] Output: 102 Explanation: After rearranging the cuboids, you can see that all cuboids have the same dimension. You can place the 11x7 side down on all cuboids so their heights are 17. The maximum height of stacked cuboids is 6 * 17 = 102.
Constraints:
n == cuboids.length1 <= n <= 1001 <= widthi, lengthi, heighti <= 100
Solutions
Solution 1: Sorting + Dynamic Programming
According to the problem description, box $j$ can be placed on box $i$ if and only if the “length, width, and height” of box $j$ are less than or equal to the “length, width, and height” of box $i$.
This problem allows us to rotate the boxes, which means we can choose any side of the box as the “height”. For any legal stacking, if we rotate each box in it to “length <= width <= height”, the stacking is still legal and can ensure the maximum height of the stacking.
Therefore, we can sort all the sides of the boxes so that each box satisfies “length <= width <= height”. Then we sort each box in ascending order.
Next, we can use dynamic programming to solve this problem.
We define $f[i]$ as the maximum height when box $i$ is at the bottom. We can enumerate each box $j$ above box $i$, where $0 \leq j < i$. If $j$ can be placed on top of $i$, then we can get the state transition equation:
\[f[i] = \max_{0 \leq j < i} \{f[j] + h[i]\}\]where $h[i]$ represents the height of box $i$.
The final answer is the maximum value of $f[i]$.
The time complexity is $O(n^2)$, and the space complexity is $O(n)$. Here, $n$ is the number of boxes.
-
class Solution { public int maxHeight(int[][] cuboids) { for (var c : cuboids) { Arrays.sort(c); } Arrays.sort(cuboids, (a, b) -> a[0] == b[0] ? (a[1] == b[1] ? a[2] - b[2] : a[1] - b[1]) : a[0] - b[0]); int n = cuboids.length; int[] f = new int[n]; for (int i = 0; i < n; ++i) { for (int j = 0; j < i; ++j) { if (cuboids[j][1] <= cuboids[i][1] && cuboids[j][2] <= cuboids[i][2]) { f[i] = Math.max(f[i], f[j]); } } f[i] += cuboids[i][2]; } return Arrays.stream(f).max().getAsInt(); } } -
class Solution { public: int maxHeight(vector<vector<int>>& cuboids) { for (auto& c : cuboids) sort(c.begin(), c.end()); sort(cuboids.begin(), cuboids.end()); int n = cuboids.size(); vector<int> f(n); for (int i = 0; i < n; ++i) { for (int j = 0; j < i; ++j) { if (cuboids[j][1] <= cuboids[i][1] && cuboids[j][2] <= cuboids[i][2]) { f[i] = max(f[i], f[j]); } } f[i] += cuboids[i][2]; } return *max_element(f.begin(), f.end()); } }; -
class Solution: def maxHeight(self, cuboids: List[List[int]]) -> int: for c in cuboids: c.sort() cuboids.sort() n = len(cuboids) f = [0] * n # f[i] meaning level-i as the base layer/level for i in range(n): for j in range(i): if cuboids[j][1] <= cuboids[i][1] and cuboids[j][2] <= cuboids[i][2]: f[i] = max(f[i], f[j]) f[i] += cuboids[i][2] # not inside if block, eg input [[38,25,45],[76,35,3]] return max(f) ############ # in python3, range() is the same as xrange() in python2 class Solution: def maxHeight(self, cuboids: List[List[int]]) -> int: """ :type cuboids: List[List[int]] :rtype: int """ for cuboid in cuboids: cuboid.sort() cuboids.append([0, 0, 0]) cuboids.sort() dp = [0]*len(cuboids) for i in range(1, len(cuboids)): for j in range(i): if all(cuboids[j][k] <= cuboids[i][k] for k in range(3)): dp[i] = max(dp[i], dp[j]+cuboids[i][2]) return max(dp) -
func maxHeight(cuboids [][]int) int { for _, c := range cuboids { sort.Ints(c) } sort.Slice(cuboids, func(i, j int) bool { a, b := cuboids[i], cuboids[j] return a[0] < b[0] || a[0] == b[0] && (a[1] < b[1] || a[1] == b[1] && a[2] < b[2]) }) n := len(cuboids) f := make([]int, n) for i := range f { for j := 0; j < i; j++ { if cuboids[j][1] <= cuboids[i][1] && cuboids[j][2] <= cuboids[i][2] { f[i] = max(f[i], f[j]) } } f[i] += cuboids[i][2] } return slices.Max(f) } -
/** * @param {number[][]} cuboids * @return {number} */ var maxHeight = function (cuboids) { for (const c of cuboids) { c.sort((a, b) => a - b); } cuboids.sort((a, b) => { if (a[0] != b[0]) return a[0] - b[0]; if (a[1] != b[1]) return a[1] - b[1]; return a[2] - b[2]; }); const n = cuboids.length; const f = new Array(n).fill(0); for (let i = 0; i < n; ++i) { for (let j = 0; j < i; ++j) { const ok = cuboids[j][1] <= cuboids[i][1] && cuboids[j][2] <= cuboids[i][2]; if (ok) f[i] = Math.max(f[i], f[j]); } f[i] += cuboids[i][2]; } return Math.max(...f); }; -
function maxHeight(cuboids: number[][]): number { for (const c of cuboids) { c.sort((a, b) => a - b); } cuboids.sort((a, b) => { if (a[0] !== b[0]) { return a[0] - b[0]; } if (a[1] !== b[1]) { return a[1] - b[1]; } return a[2] - b[2]; }); const n = cuboids.length; const f = Array(n).fill(0); for (let i = 0; i < n; ++i) { for (let j = 0; j < i; ++j) { const ok = cuboids[j][1] <= cuboids[i][1] && cuboids[j][2] <= cuboids[i][2]; if (ok) f[i] = Math.max(f[i], f[j]); } f[i] += cuboids[i][2]; } return Math.max(...f); }